Изли́шек потреби́теля (англ. consumer surplus), измеренная в денежном выражении выгода потребителя от приобретения определённого объёма продукции, возникающая вследствие наличия разницы между максимальной ценой, которую покупатель готов заплатить за покупку единицы блага, и той ценой, которую он заплатит за неё в действительности.

Происхождение термина

Понятие излишка потребителя впервые было предложено французским инженером и экономистом Ж. Дюпюи. В своей статье «О мере полезности гражданских сооружений» учёный анализирует оптимальную плату за пользование мостом. Он вводит понятие «относительная полезность» (франц. utilité relative) как меру общественного благосостояния (Дюпюи. 1999. С. 37).

Работа Дюпюи была написана в рамках дискуссии, которая велась в 1840 гг. во французской Национальной школе мостов и дорог относительно государственного финансирования общественной инфраструктуры. Идея состояла в том, чтобы предложить меру полезности, которую можно использовать для определения ценности общественных работ.

Дюпюи противоречил Ж.-Б. Сэю, который в качестве меры полезности использовал меновую стоимость товара. Дюпюи считал, что если принять точку зрения Сэя, то любое техническое изменение, ведущее к снижению цены товара, должно уменьшить и его полезность, что неверно. Наоборот, утверждал учёный, полезность товара можно оценить по тому, сколько потребитель готов потратить, чтобы получить его, или, что то же самое, по тому, сколько он готов заплатить, чтобы обойтись без него. Разницу между этой суммой и ценой, фактически уплаченной за каждую единицу товара, Дюпюи и называл относительной полезностью – и это, по сути, ныне называется потребительским излишком.

Однако для Дюпюи подсчёт этой суммы имел прикладное значение: он предполагал, что именно столько стоило бы и собирать в виде налога на финансирование общественного блага (Dupuit. 1952). Таким образом, учёный решал абсолютно прикладную задачу поиска инструмента оценки потенциальной стоимости строительства инфраструктурных объектов и в ходе решения этой задачи получил обобщение, которое используется в более широком экономическом контексте.

Для иллюстрации своей концепции Дюпюи использовал известный «парадокс воды и алмаза», описывающий явление, когда рыночная стоимость жизненно необходимых продуктов (таких как вода) значительно ниже стоимости продуктов, являющихся менее полезными (алмазы). Для разрешения парадокса часто предлагается следующий пример. Через город протекает ручей, из которого жители берут воду. Пока вода в изобилии, она не имеет меновой стоимости. Но если враг осадит город и сократит водоснабжение, вода в конце концов приобретёт такую ценность, что никто из жителей не захочет отдать литр драгоценной жидкости, даже если в обмен на него будет предложен алмаз.

Исходя из такой логики Дюпюи разработал теорию спроса, в которой кривая предельной полезности любого продукта или услуги по сути является кривой спроса на этот товар (в осях объём товара – цена). Тогда площадь под графиком этой кривой будет равняться общей полезности товара.

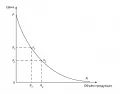Рис. 1. Кривая потребления (по Дюпюи).Рис. 1. Кривая потребления (по Дюпюи).На рис. 1 представлена кривая потребления (франц. courbe de consommation), которую Дюпюи предлагал для отражения идей спроса и уменьшения предельной полезности товара с ростом его потребления. На этом рисунке показано, что если в начальный момент времени производится $q_{1}$ единиц продукции, которые продаются по цене $p_{1}$, то общая полезность, которую получают покупатели, есть площадь под графиком, равная площади криволинейной трапеции $OP n_{1} q_{1}$. Поскольку на покупку товара в объёме $q_{1}$ потрачено $O p_{1}n_{1}q_{1}$, то разница между общей полезностью и затратами на покупку, т. е. площадь криволинейного треугольника $p_{1} P n_{1}$, есть «относительная полезность» – то, что ныне называется излишком потребителя. Площадь $n_{1}Nq_{1}$ Дюпюи называл «потерянной полезностью» (франц. utilité perdue) – из-за того, что там лежат нереализованные сделки, возможные выгоды от которых не достаются ни покупателям, ни продавцам.

На том же рисунке показано, что если объём производства блага вырастет (в случае Дюпюи речь шла о производстве инфраструктурных объектов), например, до $q_{2}$, то изменится и излишек потребителя. Он станет равен площади $P n_{2} p_{2}$, и, таким образом, можно говорить об изменении излишка, которое будет равно площади $p_{1} n_{1} n_{2} p_{2}$. Фактически это выигрыш потребителя от роста объёма потребления блага.

Критика подхода Дюпюи

Подход Дюпюи был подвергнут критике, поскольку отождествление спроса с предельной полезностью неочевидно: во-первых, оценка самих денег, которые потребители отдают за товар, очень субъективна и может изменяться от человека к человеку в зависимости от размера богатства; во-вторых, эта оценка зависит от цен на другие товары, как субституты, так и комплементы.

В 1889 г. австрийские экономисты Р. Ауспиц (1837–1906) и Р. Либен (1842–1919) попытались решить этот вопрос. Они предложили считать, что и субъективностью, и относительностью можно пренебречь, если речь идёт о небольших изменениях расходов. Тогда на небольших ценовых интервалах в качестве предпосылок можно принять следующие допущения:

• предельная полезность денег не меняется;

• вкусы остаются неизменными;

• другие цены остаются постоянными по отношению к колебаниям цены конкретного товара.

В этом случае метод Дюпюи позволяет достаточно точно оценить изменение излишка потребителя (Auspitz. 1889).

Ауспиц и Либен чётко разграничили индивидуальный и агрегированный (совокупный) излишки. В отличие от последующих рассуждений А. Маршалла (Marshall. 1961), который и сделал концепцию излишка потребителя известной и популярной, индивидуальный излишек они называли потребительской прибылью, а агрегированный рассматривали именно как полезность, которая может быть измерена в денежном выражении только тогда, когда предельная полезность денег постоянна.

Рис. 2. Идея потребительского излишка в работе Дженкина.Рис. 2. Идея потребительского излишка в работе Дженкина.Еще одна работа, предшествующая исследованию Маршалла, – доклад, представленный Ф. Дженкином (1833–1885) Эдинбургскому королевскому обществу (Jenkin. 1959). Дженкин использовал пересекающиеся графики спроса и предложения (рис. 2), которые ранее были разработаны У. С. Джевонсом для изучения принципов регулирования налогообложения. Дженкин интерпретировал область $MDN$, ныне называемую излишком потребителя, как «всю прибыль покупателей от покупки количества товаров $y$». В его понимании площадь $MDP$ – это «выручка продавцов от той же сделки» (Jenkin. 1959. P. 229). Такая трактовка позволила Дженкину (как раньше и Дюпюи) показать, что совокупные убытки, понесённые производителями и потребителями в результате введения налогов на товары, превышают фактически уплаченные налоги и увеличиваются с ростом налоговой ставки.

Метод Маршалла

Наконец, в опубликованных Маршаллом «Принципах экономической науки» (Marshall. 1961) концепция излишка потребителя получила своё современное название. Геометрически излишек потребителя представляет собой треугольную область под кривой спроса и над прямоугольной областью, площадь которой равна общей уплаченной сумме. Маршалл игнорирует проблему оценки всего графика спроса, необходимого для расчёта этой площади, поскольку, по его мнению, практическое применение этого, как и других разделов теории внутренних стоимостей, требует знания формы кривой спроса только вблизи точки $А$ (точки равновесия на кривой спроса), а для большинства целей будет достаточно знать изменения величины этой площади, которые могут быть вызваны перемещением $А$ на небольшие расстояния вдоль кривой в любом направлении.

Маршалл также признал ещё одну проблему измерения совокупного излишка, а именно необходимость суммировать излишки разных людей. Вследствие этого учёный пришёл к выводу, что формула для оценки совокупного излишка является просто общим выражением, не имеющим практического применения. Кроме того, Маршалл предполагал, что предельная полезность денег остаётся неизменной. Ограниченность такого предположения была признана, но Маршалл утверждал, что к постоянной полезности денег можно приблизиться, если потребитель тратит лишь небольшую часть своего общего дохода на конкретный товар, так что изменения его цены оказывают незначительное влияние на общую прибыль.

В общем случае, по Маршаллу, для нелинейной кривой спроса при расчёте излишка потребителя можно использовать интегрирование:

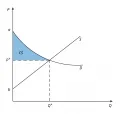$$CS= \int_{0}^{ {Q} ^{*} } D^{'} ({Q} ) \mathcal{d} {Q} - P^{*} {Q} ^{*},$$Рис. 3. Потребительский излишек как площадь под графиком спроса выше цены покупки (по Маршаллу).Рис. 3. Потребительский излишек как площадь под графиком спроса выше цены покупки (по Маршаллу).где $D^{'} ( {Q} )$ – обратная функция спроса, ${Q} ^{*}$ – приобретаемый объём блага, $P^{*}$ – установленная цена (рис. 3).

Метод Хикса

Следующую попытку решить проблему неточности измерений на больших промежутках цен предпринял Дж. Р. Хикс. В отличие от Маршалла, который предположил, что каждая денежная единица добавляет постоянную величину к общей полезности, Хикс попытался решить проблему, убрав эту предпосылку. На рис. 4 приведена иллюстрация такого подхода. На нём один под другим расположены 2 графика: один изображён в осях товаров, другой – в осях товар – цена. 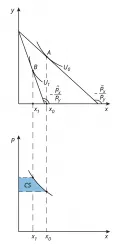Рис. 4. Построение маршаллианского спроса и изменения излишка потребителя с изменением цены.Рис. 4. Построение маршаллианского спроса и изменения излишка потребителя с изменением цены.На верхнем рисунке показано, как меняется выбор агента при росте цены товара: при цене на товар $x$, равной $\tilde{p_{x} }$, агент выбирает наилучший для него набор $A$, достигая уровня полезности $U_{0}$. При цене на товар $x$, равной $\hat{p}_{x}$, ($\hat{p}_{x}$ > $\tilde{p_{x} }$), агент выбирает наилучший для него набор $B$, достигая уровня полезности $U_{1}$. При этом цена на товар не меняется, как и доход потребителя. Однако на изменение выбора потребителя влияют как эффект замещения (изменяются относительные цены товаров), так и эффект дохода (изменяется покупательная способность одного и того же дохода). На нижнем графике строится кривая спроса на товар $x$, т. е. показана зависимость спроса на товар только от его цены. Полученная кривая представляет собой участок кривой маршаллианского спроса, который даёт возможность показать общее изменение излишка потребителя ($\Delta CS$), но не позволяет отделить изменение, вызванное отдельно эффектами замещения и дохода.

Хикс предлагает учесть изменения полезности, вызванные изменением оценки денег (покупательной способности), оценив изменение дохода, необходимое для того, чтобы компенсировать потребителю влияние изменения цены товара на его полезность.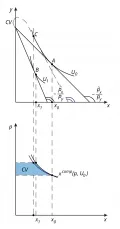Рис. 5. Построение хиксианского спроса и сравнение изменения излишка потребителя и компенсирующей вариации дохода.Рис. 5. Построение хиксианского спроса и сравнение изменения излишка потребителя и компенсирующей вариации дохода. Тогда можно было бы оценить более точно, что выигрывает, а что проигрывает потребитель при изменении цены. Эту оценку Хикс назвал компенсирующей вариацией дохода.

Такая вариация построена на рис. 5. На верхнем рисунке добавлена дополнительная пунктирная прямая, параллельная бюджетной линии с изменённым доходом. Если бы потребителю дали денег столько, чтобы он оказался на этой пунктирной прямой, он бы выбрал на ней набор $С$, т. е. отсутствие такой (компенсирующей) вариации на самом деле эквивалентно потере суммы денег, равной заштрихованной площади на нижнем графике, ограниченной кривой $x^{comp} (p, U_{0} )$. В данном случае она оказывается меньше, чем изменение потребительского излишка (площади под маршаллианским спросом).

Ещё один предложенный Хиксом вариант денежной оценки изменения благосостояния с изменением цен – эквивалентная вариация дохода. 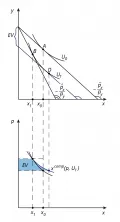Рис. 6. Построение хиксианского спроса и сравнение изменения излишка потребителя и эквивалентной вариации дохода.Рис. 6. Построение хиксианского спроса и сравнение изменения излишка потребителя и эквивалентной вариации дохода.Для её измерения нужно было бы задать вопрос, сколько денег следовало бы забрать у потребителя до изменения цены, чтобы его благосостояние было точно таким же, каким оно стало после её изменения.

На рис. 6 показан пример измерения эквивалентной вариации. Если бы не было изменения цен, а было бы снижение дохода, то такое снижение, которое для потребителя в терминах полезности эквивалентно изменению цены, можно было бы показать с помощью пунктирной бюджетной линии на верхнем рисунке. Тогда на нижнем можно было бы указать площадь, равную такой сумме денег, – площадь под кривой $x^{comp} (p, U_{1} )$, являющейся эквивалентной вариацией дохода.

Практическое применение методов оценки излишка потребителя

В целом, несмотря на проблематичность, подход Маршалла оказался наиболее привлекателен для экономистов в силу своей простоты и наглядности. С помощью маршаллианского потребительского излишка в исследованиях принято оценивать влияние на потребителя мер экономической политики, таких как введение налогов или субсидий, или определять потенциальную выгоду для потребителя от устранения монополии в отрасли и внедрения конкуренции.