Бюджетное ограничение (в задаче потребителя)
Бюдже́тное ограниче́ние (бюджетное множество), множество доступных для потребителя наборов благ при определённых ценах и доходе. Содержательно бюджетное ограничение формируется исходя из следующей логики:
В общем случае при векторе экзогенно заданных цен и заданном доходе множество допустимых товарных наборов может быть представлено так:
На бюджетном ограничении решают оптимизационную задачу выбора потребителя (максимизируют значение функции полезности).
Например, в случае двухтоварной экономики и фиксированного дохода бюджетное ограничение принимает следующий вид:
где – экзогенно заданные цены на товары; – объёмы товаров; – фиксированный экзогенно заданный доход потребителя. Тогда такое ограничение можно изобразить на плоскости в виде треугольного замкнутого множества в неотрицательном ортанте (рис. 1), а прямая, ограничивающая это множество сверху (для которой выполняется ), будет называться бюджетной линией. Для построения этой линии, как и любой прямой, необходимо знать либо координаты двух точек, либо координату одной точки и тангенс её угла наклона. Для этого проще всего выразить одну переменную (например, ) через другую (например, ). Полученное уравнение прямой будет иметь такой вид:
В данном уравнении отношение цен есть тангенс угла наклона бюджетной линии. Таким образом, как показано на рис. 2, с изменением отношения цен будет меняться наклон этой прямой, а с изменением дохода она будет сдвигаться параллельно вверх (если доход растёт) или вниз (если доход падает).
 Рис. 1. Бюджетное множество и бюджетное ограничение.
Рис. 1. Бюджетное множество и бюджетное ограничение.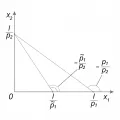 Рис. 2. Изменение бюджетного ограничения под воздействием изменения цены первого товара.Примечание к рис. 2: .
Рис. 2. Изменение бюджетного ограничения под воздействием изменения цены первого товара.Примечание к рис. 2: .
Существует множество стандартных моделей формирования дохода, соответствующих реальным ситуациям, а также интерпретаций товаров.
Так, доход может формироваться не как фиксированная сумма (например, заработная плата в месяц), а как стоимость имеющихся у экономического агента товаров, которые называют «первоначальным запасом». Пусть, например, у агента в двухтоварной экономике существует ненулевой первоначальный запас каждого блага, равный . Тогда сумма денег, которой может распоряжаться агент, фактически равна стоимости данного первоначального запаса, т. е. . Преобразованное бюджетное ограничение будет выглядеть следующим образом:
Поскольку при подстановке в данное бюджетное ограничение вместо набора товаров первоначального запаса неравенство выполняется как верное равенство, это означает, что при изменении цен все бюджетные линии будут проходить через точку первоначального запаса (рис. 3).
 Рис. 3. Изменение бюджетного ограничения с первоначальным запасом под воздействием изменения цены первого товара.Примечание к рис. 3: .
Рис. 3. Изменение бюджетного ограничения с первоначальным запасом под воздействием изменения цены первого товара.Примечание к рис. 3: .
Если рассмотреть в качестве одного из товаров время, а в качестве его стоимости – заработную плату в час, можно получить ещё одну интерпретацию бюджетного ограничения – множества, на котором потребитель будет делать выбор между временем труда и отдыха. Пусть в день у каждого человека есть некоторый временной запас (), который он может распределить между отдыхом () и работой (). Работая, агент получает заработную плату в час (); это означает, что час отдыха оценивается в ту же самую сумму денег, что и час работы, но это уже будет стоимостью потребления отдыха. Таким образом, ставка заработной платы есть альтернативная стоимость отдыха.
Кроме отдыха, агенту требуются еда, жильё, другие товары и услуги, которые можно объединить в агрегированное благо (стоимость всех остальных товаров и услуг, помимо отдыха). Если никаких нетрудовых доходов у потребителя нет, то покупать товары и услуги он сможет, только если будет хотя бы часть времени работать: , при том что .
Соответственно, бюджетное ограничение можно переписать в следующем виде:где слева приведены все расходы (на отдых и товары), а справа – стоимость всего запаса времени человека, или полный (предполагаемый) доход потребителя. С ростом заработной платы такое бюджетное множество будет расширяться, но только за счёт включения в него новых объёмов товаров и услуг: запас времени, будучи фиксированным, расширен быть не сможет, поскольку время нельзя докупить (рис. 4).
 Рис. 4. Изменение бюджетного ограничения с первоначальным запасом в виде времени под воздействием изменения ставки заработной платы.Примечание к рис. 4: .
Рис. 4. Изменение бюджетного ограничения с первоначальным запасом в виде времени под воздействием изменения ставки заработной платы.Примечание к рис. 4: .
Бюджетное ограничение с первоначальным запасом также может быть интерпретировано в терминах т. н. двухпериодной модели, в которой делается попытка учесть возможность изменения дохода за счёт кредита или депозита. В такой модели предполагается, что агент живёт ровно 2 периода, в каждый из которых получает некоторый доход: – в первом периоде и – во втором.
Агент имеет возможность, например, потратить в первом периоде не всю заработанную сумму денег, а только её часть: ; оставшуюся же сумму () – положить на депозитный счёт в банке под процентов. Тогда во втором периоде максимальная величина его расходов может составить . В преобразованном виде это уравнение выглядит следующим образом:
Такой вид уравнения бюджетной линии позволяет интерпретировать как отношение цен потребления в первом и во втором периодах, т. е. относительную стоимость межпериодного потребления.
Возможна и ситуация, при которой в первом периоде агент решает потратить денег больше, чем заработал. Для этого ему нужно взять в кредит сумму по ставке . Однако это означает, что во втором периоде этот кредит нужно будет отдавать, т. е. максимальные расходы агента составят . Аналогичные рассуждения позволяют получить отношение цен межпериодного потребления, равное .
Бюджетная линия, ограничивающая межпериодное бюджетное ограничение, изображена на рис. 5. При этом часто процент по кредиту выше, чем по депозиту, что даёт характерный излом бюджетной линии в точке первоначального запаса.
 Рис. 5. Бюджетное множество, ограниченное межпериодной бюджетной линией. Ситуация разных процентов по кредиту и депозиту.Таким образом, вид и содержательная интерпретация бюджетного множества зависят от конкретной модели. Помимо двухтоварных экономик, оно используется и при моделировании экономик с большим количеством товаров, но поскольку любая такая модель может быть переформулирована как модель с одним (интересующим исследователя) товаром и агрегированным благом (стоимостью всех остальных товаров и услуг), в целом графической интерпретации бюджетного ограничения в большинстве случаев достаточно.
Рис. 5. Бюджетное множество, ограниченное межпериодной бюджетной линией. Ситуация разных процентов по кредиту и депозиту.Таким образом, вид и содержательная интерпретация бюджетного множества зависят от конкретной модели. Помимо двухтоварных экономик, оно используется и при моделировании экономик с большим количеством товаров, но поскольку любая такая модель может быть переформулирована как модель с одним (интересующим исследователя) товаром и агрегированным благом (стоимостью всех остальных товаров и услуг), в целом графической интерпретации бюджетного ограничения в большинстве случаев достаточно.
