Аналитическая геометрия
Аналити́ческая геоме́трия, раздел геометрии, в котором геометрические объекты (прямые, плоскости, линии и поверхности второго порядка) исследуются средствами алгебры на основе метода координат.
Возникновение в 17 в. метода координат связано с развитием астрономии, механики и техники. Изложение этого метода и основ аналитической геометрии было дано Р. Декартом в его «Геометрии» (1637). Основные идеи метода были известны также его современнику П. Ферма. Дальнейшая разработка аналитической геометрии связана с трудами Г. В. Лейбница, И. Ньютона и особенно Л. Эйлера. Средствами аналитической геометрии пользовался Ж. Л. Лагранж при построении аналитической механики и Г. Монж в дифференциальной геометрии. Долгое время для аналитической геометрии было принято название «декартова геометрия», которое ввёл И. Бернулли (1692).
Сущность метода координат заключается в следующем. Пусть на плоскости заданы две взаимно перпендикулярные прямые и (рис. 1).
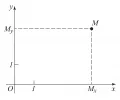 Рис. 1. Эти прямые с указанием направления, начала координат и масштабной единицы образуют т. н. декартову систему координат на плоскости. Прямые и называются соответственно осью абсцисс и осью ординат. Положение любой точки на плоскости по отношению к этой системе можно определить следующим образом. Пусть и – проекции на и , а числа и – величины отрезков и ; величина отрезка равна длине этого отрезка, взятой со знаком плюс, если направление от к совпадает с направлением на прямой , и со знаком минус в противоположном случае, величина определяется аналогично. Числа и называются декартовыми прямоугольными координатами (прямоугольными координатами, декартовыми координатами) точки в системе . Обычно называется абсциссой, а – ординатой точки . Для обозначения точки с абсциссой и ординатой пользуются символом или . Координаты точки определяют её положение относительно системы .
Рис. 1. Эти прямые с указанием направления, начала координат и масштабной единицы образуют т. н. декартову систему координат на плоскости. Прямые и называются соответственно осью абсцисс и осью ординат. Положение любой точки на плоскости по отношению к этой системе можно определить следующим образом. Пусть и – проекции на и , а числа и – величины отрезков и ; величина отрезка равна длине этого отрезка, взятой со знаком плюс, если направление от к совпадает с направлением на прямой , и со знаком минус в противоположном случае, величина определяется аналогично. Числа и называются декартовыми прямоугольными координатами (прямоугольными координатами, декартовыми координатами) точки в системе . Обычно называется абсциссой, а – ординатой точки . Для обозначения точки с абсциссой и ординатой пользуются символом или . Координаты точки определяют её положение относительно системы .
Пусть на плоскости с прямоугольной системой координат задана некоторая линия . Используя понятие координат точек, можно ввести понятие уравнения линии относительно системы как соотношения вида , которому удовлетворяют координаты и любой точки , расположенной на , и не удовлетворяют координаты точек, не лежащих на . Если, например, линия является окружностью радиуса с центром в начале координат , то уравнение является уравнением рассматриваемой окружности (рис. 2).
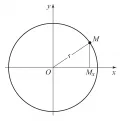 Рис. 2.Если точка лежит на окружности, то по теореме Пифагора для треугольника справедливо равенство . Если же точка не лежит на окружности, то .
Рис. 2.Если точка лежит на окружности, то по теореме Пифагора для треугольника справедливо равенство . Если же точка не лежит на окружности, то .
Основная идея метода координат состоит в том, что геометрические свойства линии исследуются с помощью изучения свойств уравнения этой линии аналитическими и алгебраическими средствами. Например, для нахождения числа точек пересечения окружности радиуса и данной прямой линии (рис. 3) метод координат применяется следующим образом.
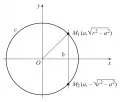 Рис. 3.Систему координат выбирают так, чтобы её начало находилось в центре окружности, а ось была направлена перпендикулярно прямой . Так как прямая перпендикулярна оси , абсцисса любой точки этой прямой равна некоторой постоянной , т. е. уравнение прямой имеет вид . Координаты любой точки пересечения окружности (уравнение которой имеет вид ) и прямой удовлетворяют уравнениямСледовательно, геометрический вопрос о числе точек пересечения прямой и окружности сводится к аналитическому вопросу о числе решений системы алгебраических уравнений . Решая эту систему, получаюттаким образом, окружность и прямая пересекаются в двух точках при (этот случай изображён на рис. 3), имеют одну общую точку при (в этом случае прямая касается окружности ) и не имеют общих точек при .
Рис. 3.Систему координат выбирают так, чтобы её начало находилось в центре окружности, а ось была направлена перпендикулярно прямой . Так как прямая перпендикулярна оси , абсцисса любой точки этой прямой равна некоторой постоянной , т. е. уравнение прямой имеет вид . Координаты любой точки пересечения окружности (уравнение которой имеет вид ) и прямой удовлетворяют уравнениямСледовательно, геометрический вопрос о числе точек пересечения прямой и окружности сводится к аналитическому вопросу о числе решений системы алгебраических уравнений . Решая эту систему, получаюттаким образом, окружность и прямая пересекаются в двух точках при (этот случай изображён на рис. 3), имеют одну общую точку при (в этом случае прямая касается окружности ) и не имеют общих точек при .
В аналитической геометрии на плоскости исследуются т. н. алгебраические линии 1-го и 2-го порядков; эти линии в прямоугольных координатах определяются соответственно алгебраическими уравнениями 1-й и 2-й степеней. На плоскости линии 1-го порядка суть прямые, и обратно, каждая прямая определяется алгебраическим уравнением 1-й степенилинии 2-го порядка определяются уравнениями видагде – некоторые числа.
Для исследования и классификации линий 2-го порядка вначале выбирается такая прямоугольная система координат, в которой уравнение линии имеет наиболее простой вид, а затем проводится исследование этого уравнения. О линиях 2-го порядка см. в статьях Гипербола, Конические сечения, Парабола, Эллипс.
В пространстве прямоугольные координаты , и (соответственно абсцисса, ордината и аппликата) точки вводятся по аналогии с плоским случаем (рис. 4).
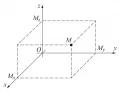 Рис. 4.Каждой поверхности в пространстве можно сопоставить её уравнение относительно системы координат . Например, уравнение сферы радиуса с центром в начале координат имеет видГеометрические свойства поверхности исследуются с помощью изучения свойств уравнения этой поверхности аналитическими и алгебраическими средствами. Линию в пространстве задают как линию пересечения двух поверхностей и . Если и – уравнения поверхностей и , то пара этих уравнений, рассматриваемая совместно, представляет собой уравнение линии . Например, прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. Так как плоскости в пространстве определяются уравнениями видато прямую можно задать парой уравнений такого вида, рассматриваемых совместно. Таким образом, метод координат может применяться и для исследования линий в пространстве. В пространстве систематически исследуются т. н. алгебраические поверхности 1-го и 2-го порядков. Алгебраическими поверхностями 1-го порядка являются лишь плоскости. Поверхности 2-го порядка определяются уравнениями видагде – некоторые числа. Так же как в случае плоскости, для исследования и классификации этих поверхностей вначале выбирается такая прямоугольная система координат, в которой уравнение поверхности имеет наиболее простой вид, а затем проводится исследование этого уравнения. О поверхностях 2-го порядка см. в статьях Гиперболоид, Параболоид, Эллипсоид.
Рис. 4.Каждой поверхности в пространстве можно сопоставить её уравнение относительно системы координат . Например, уравнение сферы радиуса с центром в начале координат имеет видГеометрические свойства поверхности исследуются с помощью изучения свойств уравнения этой поверхности аналитическими и алгебраическими средствами. Линию в пространстве задают как линию пересечения двух поверхностей и . Если и – уравнения поверхностей и , то пара этих уравнений, рассматриваемая совместно, представляет собой уравнение линии . Например, прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. Так как плоскости в пространстве определяются уравнениями видато прямую можно задать парой уравнений такого вида, рассматриваемых совместно. Таким образом, метод координат может применяться и для исследования линий в пространстве. В пространстве систематически исследуются т. н. алгебраические поверхности 1-го и 2-го порядков. Алгебраическими поверхностями 1-го порядка являются лишь плоскости. Поверхности 2-го порядка определяются уравнениями видагде – некоторые числа. Так же как в случае плоскости, для исследования и классификации этих поверхностей вначале выбирается такая прямоугольная система координат, в которой уравнение поверхности имеет наиболее простой вид, а затем проводится исследование этого уравнения. О поверхностях 2-го порядка см. в статьях Гиперболоид, Параболоид, Эллипсоид.
В аналитической геометрии эффективно используется векторная алгебра. Естественное обобщение аналитической геометрии на случай многомерных векторных пространств составляет особый раздел математики – линейную алгебру.
