Декартова система координат
Дека́ртова систе́ма координа́т, прямолинейная система координат на плоскости или в пространстве, в которой положение точки может быть определено как её проекции на фиксированные прямые, пересекающиеся в одной точке, называемой началом координат. Эти проекции называются координатами точки, а прямые – осями координат.
В общем случае на плоскости декартова система координат (аффинная система координат) задаётся точкой (началом координат) и упорядоченной парой приложенных к ней не лежащих на одной прямой векторов и (базисных векторов). Прямые, проходящие через начало координат в направлении базисных векторов, называют осями координат данной декартовой системы координат. Первая, определяемая вектором , называется осью абсцисс (или осью ), вторая – осью ординат (или осью ). Сама декартова система координат обозначается или . Декартовыми координатами точки (рис. 1)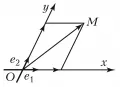 Рис. 1. Декартова система координат на плоскости. в декартовой системе координат называется упорядоченная пара чисел, которые являются коэффициентами разложения вектора по базису , т. е. и таковы, что . Число , , называется абсциссой, число , , – ординатой точки . Если – координаты точки , то пишут .
Рис. 1. Декартова система координат на плоскости. в декартовой системе координат называется упорядоченная пара чисел, которые являются коэффициентами разложения вектора по базису , т. е. и таковы, что . Число , , называется абсциссой, число , , – ординатой точки . Если – координаты точки , то пишут .
Если на плоскости введены две декартовы системы координат и так, что векторы базиса выражены через векторы базиса формулами и точка имеет в декартовой системе координат координаты , то координаты точки в декартовой системе координат и координаты той же точки в декартовой системе координат связаны соотношениями Декартову систему координат называют прямоугольной, если базис ортонормированный, т. е. векторы и взаимно перпендикулярны и имеют длины, равные единице (векторы и называют в этом случае ортами). В прямоугольной декартовой системе координат координаты и точки суть величины ортогональных проекций точки на оси и соответственно. В прямоугольной декартовой системе координат расстояние между точками и равно
Формулы перехода от одной прямоугольной декартовой системы координат к другой прямоугольной декартовой системе координат , начало которой , имеют вид или В первом случае система образуется поворотом базисных векторов на угол и последующим переносом начала координат в точку (рис. 2),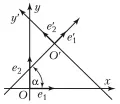 Рис. 2. Переход от одной декартовой системы координат к другой поворотом базисных векторов на угол α и последующим переносом начала координат O в точку O′. а во втором случае – поворотом базисных векторов на угол , последующим отражением оси, содержащей вектор относительно прямой, несущей вектор , и переносом начала координат в точку (рис. 3).
Рис. 2. Переход от одной декартовой системы координат к другой поворотом базисных векторов на угол α и последующим переносом начала координат O в точку O′. а во втором случае – поворотом базисных векторов на угол , последующим отражением оси, содержащей вектор относительно прямой, несущей вектор , и переносом начала координат в точку (рис. 3).
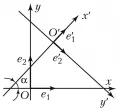 Рис. 3. Переход от одной декартовой системы координат к другой поворотом базисных векторов на угол α, последующим отражением и переносом начала координат O в точку O′.Иногда используются косоугольные декартовы системы координат, отличающиеся от прямоугольной тем, что угол между единичными базисными векторами не является прямым.
Рис. 3. Переход от одной декартовой системы координат к другой поворотом базисных векторов на угол α, последующим отражением и переносом начала координат O в точку O′.Иногда используются косоугольные декартовы системы координат, отличающиеся от прямоугольной тем, что угол между единичными базисными векторами не является прямым.
Аналогично определяется общая декартова система координат (аффинная система координат) в пространстве: задаётся точка – начало координат и упорядоченная тройка приложенных к ней не лежащих в одной плоскости векторов (базисных векторов). Как и в случае плоскости, определяются оси координат – ось абсцисс (ось ), ось ординат (ось ) и ось аппликат (ось ) (рис. 4).
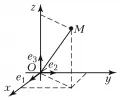 Рис. 4. Декартова система координат в трёхмерном пространстве.Декартова система координат в пространстве обозначается (или ). Плоскости, проходящие через пары осей координат, называются координатными плоскостями. Декартова система координат в пространстве называется правой, если поворот от оси к оси совершается в направлении, противоположном движению часовой стрелки, если смотреть на плоскость из какой-нибудь точки положительной полуоси ; в противоположном случае декартова система координат называется левой. Если базисные векторы имеют длины, равные единице, и попарно перпендикулярны, то декартова система координат называется прямоугольной. Положение одной прямоугольной декартовой системы координат в пространстве относительно другой прямоугольной декартовой системы координат с той же ориентацией определяется тремя эйлеровыми углами.
Рис. 4. Декартова система координат в трёхмерном пространстве.Декартова система координат в пространстве обозначается (или ). Плоскости, проходящие через пары осей координат, называются координатными плоскостями. Декартова система координат в пространстве называется правой, если поворот от оси к оси совершается в направлении, противоположном движению часовой стрелки, если смотреть на плоскость из какой-нибудь точки положительной полуоси ; в противоположном случае декартова система координат называется левой. Если базисные векторы имеют длины, равные единице, и попарно перпендикулярны, то декартова система координат называется прямоугольной. Положение одной прямоугольной декартовой системы координат в пространстве относительно другой прямоугольной декартовой системы координат с той же ориентацией определяется тремя эйлеровыми углами.
Декартова система координат названа по имени Р. Декарта, хотя в его сочинении «Геометрия» (1637) рассматривалась косоугольная система координат, в которой координаты точек могли быть только положительными. В издании 1659–1661 гг. к «Геометрии» приложена работа голландского математика И. Худде, в которой впервые допускаются как положительные, так и отрицательные значения координат. Пространственную декартову систему координат ввёл французский математик Ф. де Лаир (1679). В начале 18 в. установились обозначения для декартовых координат.
