Эл­лип­ти­че­ский параболоид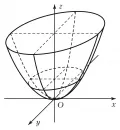. БРЭ. Т. 25.Эл­лип­ти­че­ский параболоид. БРЭ. Т. 25.Параболо́ид (от парабола и ...ид), незамкнутая нецентральная поверхность второго порядка; существуют два вида параболоидов – эллиптический параболоид и гиперболический параболоид. Оба они могут быть представлены как поверхности, описываемые при движении одной (подвижной) параболы вдоль другой (неподвижной) так, что вершина подвижной параболы скользит по неподвижной, а плоскость и ось подвижной параболы остаются параллельными сами себе. Эллиптический параболоид получается, если обе 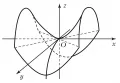Ги­пер­бо­ли­че­ский параболоид.Ги­пер­бо­ли­че­ский параболоид.параболы обращены вогнутостью в одну сторону, гиперболический параболоид – если параболы обращены вогнутостью в разные стороны, поэтому гиперболический параболоид имеет вид седла.

В прямоугольной системе координат $Oxyz$ с началом в вершине параболоида, ось $Oz$ которой является осью симметрии параболоида, а плоскости $zOx$ и $Oyz$ – плоскостями симметрии параболоида, уравнение параболоида имеет т. н. канонический вид:

$\dfrac{x^2}{p}+\dfrac{y^2}{q}=2z$для эллиптического параболоида и
$\dfrac{x^2}{p} =\dfrac{x^2}{q} =2z$для гиперболического параболоида, где $p>0$, $q>0$ – параметры.

Сечения эллиптического параболоида, параллельные плоскости $Oxy$, – эллипсы; сечения, параллельные оси $Oz$, – параболы. Если $p=q$, то параболоид является параболоидом вращения, который получается вращением параболы $x^2=2pz$, лежащей в плоскости $Oxy$, вокруг своей оси. Сечения плоскостями $Oxz$ и $Oyz$ – параболы: $x^2=2pz$, $y=0$ (неподвижная) и $y^2=2qz$, $x=0$ (подвижная).

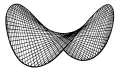Гиперболический параболоид, об­ра­зо­ван­ный дву­мя се­мей­ст­ва­ми пря­мых. БРЭ. Т. 25.Гиперболический параболоид, об­ра­зо­ван­ный дву­мя се­мей­ст­ва­ми пря­мых. БРЭ. Т. 25.

Сечения гиперболического параболоида плоскостями $Oxz$ и $Oyz$ – параболы: $x^2=2pz$, $y=0$ (неподвижная) и $y^2=-2qz$, $y=0$ (подвижная). Сечения плоскостями, параллельными плоскости $Oxy$, – гиперболы (при $z=0$ – пара пересекающихся прямых). Через каждую точку гиперболического параболоида проходят две прямые, целиком принадлежащие его поверхности, – прямолинейные образующие, таким образом, гиперболический параболоид – линейчатая поверхность, образованная двумя семействами прямых.