Линия
Ли́ния (от лат. linea, буквально – льняная нить; линия, черта), геометрическое понятие, определение которого в различных разделах математики осуществляется по-разному.
В элементарной геометрии рассматриваются прямые линии, отрезки прямых, ломаные линии, составленные из отрезков, и некоторые кривые линии; каждый вид кривых линий определяется тем или иным специальным способом (например, окружность определяется как множество точек, находящихся на заданном расстоянии от некоторой точки – центра окружности). Иногда дают определение линии как границы части поверхности или траектории движущейся точки. Однако в рамках элементарной геометрии эти определения не получают отчётливой формулировки.
Представление о линии как о траектории движущейся точки может быть сделано строгим при помощи параметрического представления линии. Например, вводя на плоскости прямоугольные координаты , можно параметрически задать окружность радиуса с центром в начале координат уравнениями . Когда параметр пробегает значения , точки описывают на плоскости окружность. Вообще, линии на плоскости задают параметрическими уравнениями
где и – функции, непрерывные на конечном или бесконечном интервале числовой оси . Каждому значению параметра (из интервала ) сопоставляется точка , координаты которой задаются этими уравнениями. Линия, заданная этими уравнениями, есть множество точек, соответствующих всевозможным значениям из ; при этом точки рассматриваются в определённом порядке, а именно: если точка соответствует значению параметра , а точка – значению , то считается предшествующей , если меньше . Точки, отвечающие различным значениям параметра, считаются различными.
Аналогично, в трёхмерном пространстве линия задаётся параметрически тремя равенствами , , где , – действительные функции, непрерывные на каком-либо интервале. В произвольном топологическом пространстве (которое, в частности, может быть плоскостью, трёхмерным пространством, функциональным пространством и т. п.) линии параметрически задаются равенствами вида , где – функция действительного переменного , непрерывная на каком-либо интервале, значения которой суть точки пространства . Считают, что два параметрических представления задают одну и ту же линию, если они определяют одно и то же множество точек и один и тот же порядок их следования.
В математическом анализе и топологии рассматривают обычно случай, когда область изменения параметра есть отрезок . В этом случае условие того, что два параметрических представления
задают одну и ту же линию, заключается в существовании непрерывной и строго возрастающей функции , для которой
Такое понимание термина «линия» естественно в большинстве задач анализа (например, в теории криволинейных интегралов) и механики. При возрастании от до переменная точка , соответствующая данному значению , может проходить через одну и ту же точку линии один или несколько раз (при различных значениях параметра . В первом случае точка кривой называется простой, во втором – кратной.
Из аналитической геометрии известен и другой способ задания линии на плоскости уравнением , а в пространстве – двумя уравнениями . В случае плоскости часто рассматриваются алгебраические линии (кривые) – линии, определяемые уравнением , где – целая алгебраическая функция, т. е. многочлен степени . В этом случае два многочлена и определяют одну и ту же линию тогда и только тогда, когда существует такая постоянная , что выполняется тождество
Все многочлены, определяющие одну и ту же линию, имеют одну и ту же степень , называемую порядком соответствующей линии. Например, в аналитической геометрии принято считать, что уравнение определяет линии 2-го порядка, а именно дважды взятую прямую . Линиями 1-го порядка являются прямые. Часто целесообразно ограничиваться рассмотрением неприводимых алгебраических линий, т. е. таких линий, для которых многочлен не допускает представления , где и – многочлены, отличные от постоянных. Далее имеется в виду только этот случай.
Говорят, что точка кривой имеет кратность , если разложение функции по степеням переменных и начинается с членов степени (по совокупности переменных и ). В случае , т. е. в случае двойной точки,
где многоточие означает, что далее следуют члены высших порядков. При помощи дискриминанта можно определить тип двойной точки (см. Особая точка кривой).
При изучении алгебраической линии часто, наряду с точками евклидовой действительной плоскости (или пространства), рассматриваются точки бесконечно удалённые и мнимые. При таком подходе (и надлежащем учёте кратности пересечения) становится верным, например, утверждение, что две линии порядков и пересекаются в точках. В случае это приводит к возможности определить порядок линии как число точек её пересечения с некоторой прямой.
Рассмотренные выше уточнения и обобщения понятия линии существенно связаны с соответствующим алгебраическим и аналитическим аппаратом. В отличие от этого, современная топология рассматривает представление о линии как о множестве точек независимо от алгебраических или аналитических способов задания этого множества.
Если исходить из параметрического задания линии на плоскости в виде множества точек, координаты которых определяются равенствами и , где и – непрерывные функции, а пробегает отрезок , но интересоваться только полученным множеством точек без учёта порядка их следования, то приходят к понятию линии, сформулированному в 1880-х гг. М. Э. К. Жорданом (кривая Жордана), т. е. к понятию линии как непрерывного образа отрезка. Оказывается, что таким непрерывным образом отрезка может быть квадрат, треугольник и т. п. (кривая Пеано). Взаимно однозначный непрерывный образ отрезка называют простой дугой или жордановой дугой. Взаимно однозначный непрерывный образ окружности называют простой замкнутой линией. Простые дуги и простые замкнутые линии не исчерпывают, однако, точечных множеств, заслуживающих наименования линий.
Избегая и чрезмерной общности, и чрезмерного сужения понятия линии, в современной топологии пользуются понятием линии, введённым в 1921 г. П. С. Урысоном, который определяет линию (кривую) как произвольный континуум размерности единица. Континуум имеет размерность единица, если при любом он может быть представлен в виде суммы конечного числа замкнутых множеств диаметра, меньшего , обладающих тем свойством, что никакие три из этих замкнутых множеств не имеют общей точки. Континуум, лежащий на плоскости, будет линией в смысле Урысона тогда и только тогда, когда он не содержит внутренних точек. Этим свойством характеризовал линии, лежащие на плоскости, Г. Кантор (1870-е гг.). Хотя определение Кантора применимо только к линиям, лежащим на плоскости, иногда и общие линии в смысле Урысона называют канторовыми кривыми.
Ещё математики древности рассматривали ряд замечательных алгебраических линий, среди которых линии второго порядка, линии более высоких порядков, а также трансцендентные (неалгебраические) линии. Систематическое изучение линий и их классификация стали возможными после создания аналитической геометрии.
Из линий 3-го порядка наиболее известны следующие.
Локон Аньези (или верзиера) – плоская алгебраическая кривая, декартовы прямоугольные координаты точек которой связаны уравнением , где постоянная (рис. 1). Исследование этой линии связано с именем итальянского математика М. Аньези (1748).
Декартов лист – кривая, уравнение которой в декартовых прямоугольных координатах есть , где постоянная (рис. 2). Впервые кривая определяется в переписке Р. Декарта и П. Ферма (1638).
Кубическая парабола – кривая, уравнение которой в прямоугольных декартовых координатах есть , где – действительное число, .
Полукубическая парабола (парабола Нейля) – кривая, уравнение которой в прямоугольных декартовых координатах есть , где постоянная (рис. 3). Её параметрические уравнения суть , . Названа по имени изучавшего её английского математика У. Нейля (1657).
Трезубец – кривая, уравнение которой в прямоугольных декартовых координатах есть , где – положительные постоянные (рис. 4). Кривая имеет две бесконечные ветви и одну асимптоту. Левая ветвь кривой (т. н. парабола Декарта) описана Р. Декартом (1637). Кривая исследовалась И. Ньютоном (1704), предложившим название.
Из линий 4-го порядка наиболее известны следующие.
Лемниската Бернулли – кривая, имеющая форму восьмёрки (рис. 5); геометрическое место точек, для которых произведение расстояний до фокусов и равно . Уравнение в прямоугольных координатах есть и в полярных координатах. Впервые рассматривалась Я. Бернулли (1694). Лемниската является частным случаем овала Кассини.
Овал Кассини – кривая, уравнение в прямоугольных координатах которой есть
где и – положительные числа. Для точек этой кривой (рис. 6) произведение расстояний до двух фиксированных точек и является постоянной величиной . Форма кривой, симметричной относительно осей и , зависит от соотношения между параметрами и . При эта кривая – эллипсообразный овал (кривая а на рис. 6), при – «овал с талией» (кривая б, рис. 6), при – лемниската Бернулли (кривая в, рис. 6), при овал Кассини состоит из двух овалов (кривая г, рис. 6). Рассмотрены Дж. Кассини (17 в.).
Декартов овал – плоская кривая (рис. 7), расстояния и для каждой точки до двух фиксированных точек и (фокусов) связаны неоднородным линейным уравнением , где и – положительные числа. Эту линию можно задать однородным линейным уравнением , где – расстояние до третьего фокуса , лежащего на прямой, проходящей через и . В прямоугольных декартовых координатах уравнение этой линии имеет вид , где – длина отрезка . При и декартов овал представляет собой эллипс, при и – гиперболу и при – улитку Паскаля. Впервые исследовались Р. Декартом (1637).
Кардиоида – кривая, уравнение которой в прямоугольных координатах есть
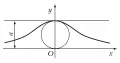
где , и в полярных координатах. Кардиоида описывается точкой окружности (рис. 8) радиуса , катящейся по окружности того же радиуса. Кардиоида является частным случаем улитки Паскаля.
Из линий более высоких порядков наиболее известны кривые Ламе и астроиды.
Кривая Ламе – линия, уравнение которой в прямоугольных координатах есть
где и – положительные числа, – рациональное число, причём и – взаимно простые числа. Приведены примеры кривых Ламе для , чётного и нечётного (рис. 9, а) и 0, чётного и нечётного (рис. 9, б). При порядок кривой есть , и он равен при . Эти кривые рассмотрены Г. Ламе (1818).
Астроида – плоская алгебраическая кривая 6-го порядка, которая описывается точкой окружности радиуса , катящейся по внутренней стороне неподвижной окружности радиуса (рис. 10). Уравнение астроиды в прямоугольных координатах есть , где – радиус неподвижной окружности.
Большой класс линий составляют трансцендентные линии. К ним относятся графики тригонометрических функций, показательной функции, логарифмической функции, гиперболических функций, а также трактриса, узорная кривая, цепная линия, циклоида. К циклоиде по способу построения примыкает класс циклоидальных кривых, которые могут быть как трансцендентными, так и алгебраическими. Например, астроида является циклоидальной кривой.
Среди трансцендентных линий выделяют спирали. К спиралям относится гиперболическая спираль (рис. 11) – кривая, описываемая точкой , движущейся по вращающейся прямой так, что её расстояние от центра вращения меняется обратно пропорционально углу поворота. Уравнение в полярных координатах есть . Кривая состоит из двух ветвей, соответствующих положительным и отрицательным значениям .
Особый класс составляют производные от других кривых, т. е. полученные из исходных при помощи некоторых операций, например линия погони, эволюта, эвольвента.
Важнейшей числовой характеристикой протяжённости линии является длина. Длиной отрезка прямой называется расстояние между его концами, измеренное с помощью какого-либо отрезка, принятого за единицу длины. Длина ломаной линии определяется как сумма длин её звеньев. Длина простой дуги – предел длин, вписанных в эту дугу ломаных, когда число звеньев неограниченно увеличивается и максимум их длин стремится к нулю. Например, длина окружности может быть получена как предел периметров правильных вписанных многоугольников при неограниченном увеличении числа их сторон и равна , где – радиус окружности. Длина непрерывной кривой, состоящей из конечного числа простых дуг, равна сумме длин этих дуг. Всякая непрерывная кривая имеет длину, конечную или бесконечную. Если длина кривой конечна, то она называется спрямляемой.
График функции (рис. 12)
даёт пример неспрямляемой кривой; для этой линии длины вписанных ломаных неограниченно растут, когда длины звеньев стремятся к нулю.
Длина плоской кривой, заданной в прямоугольных координатах уравнением , , где имеет непрерывную производную , выражается интегралом
Если кривая задана в параметрической форме , , , то её длина выражается равенством
Длина спрямляемой кривой не зависит от способа параметризации. Длина пространственной кривой, заданной в параметрической форме , , , , выражается равенством
а в случае -мерного пространства
К вычислению длины кривой при помощи предельного перехода по длинам ломаных прибегали, по существу, ещё математики древности. Для них, однако, этот предельный переход был лишь способом вычисления длины кривой, а не определением понятия длины, т. к. последнее им представлялось, по-видимому, одним из исходных математических понятий. Необходимость определения понятия длины кривой была осознана в 1-й половине 19 в. Ясность в вопросе о длине кривой появилась лишь после работ М. Э. К. Жордана (1880). В дифференциальной геометрии определяется также длина на поверхности или в произвольном римановом пространстве.