Парабола

Пара́бола (греч. παραβολή – приложение, сравнение, сближение), множество точек $M=M(x,y)$ плоскости (рис. 1), для которых расстояние $r=FM$ до определённой точки $F(p/2, 0)$ этой плоскости (фокуса параболы) равно расстоянию $d=DM$ до определённой 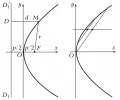Рис. 1 и 2. Парабола.

прямой $D_1D'_1$ (директрисы параболы). Прямая, проходящая через фокус $F$ перпендикулярно директрисе $D_1D'_1$, называется осью параболы, точка пересечения параболы с осью – вершиной параболы.

В прямоугольной системе координат $Oxy$ с началом в вершине параболы и осью $Ox$, направленной по оси параболы от директрисы к фокусу, уравнение параболы имеет т. н. канонический вид
$y^2=2px,$где $p$ (фокальный параметр) – расстояние от фокуса до директрисы или половина длины хорды, проходящей через фокус перпендикулярно оси.

Парабола – нецентральная линия второго порядка. Она состоит из одной бесконечной ветви, симметричной относительно оси. Эксцентриситет параболы $e=1$. Диаметр параболы – прямая, проходящая через середины параллельных хорд (рис. 2).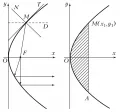Рис. 3 и 4. Парабола.

Касательная $TM$ и нормаль $NM$ к параболе в точке $M$ (рис. 3) являются биссектрисами углов

между фокальным радиус-вектором $FM$ и диаметром $DM$. Поэтому если в фокусе параболы поместить источник света, то исходящие из него лучи после зеркального отражения от кривой образуют пучок, параллельный её оси.

Радиус кривизны параболы в точке $M(x,y)$

$R=(p+2x)^{3/2}/\sqrt p;$в вершине $R=p$.

Площадь сегмента $AOM$ (рис. 4) равна $4x_1y_1/3$.

В полярной системе координат (полюс в фокусе параболы, полярная ось направлена по оси параболы) уравнение параболы имеет вид

$\rho=\dfrac{p}{1-\cos \varphi}.$Уравнение параболы с вертикальной осью (рис. 5): 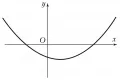Рис. 5. Парабола.

$y=ax^2+bx+c$(фокальный параметр $p= ∣a∣/2$); при $a>0$ парабола обращена вершиной вниз, при $a<0$ – вершиной вверх, координаты вершины

$x_0=\dfrac{b}{2a}, \qquad y_0=\dfrac{4ac-b^2}{4a}.$Иногда параболу $n$-го порядка называют графиком степенной функции $y=ax^n$.

Название «парабола» ввёл Аполлоний Пергский (около 200 до н. э.), рассматривавший параболу как одно из конических сечений.