Тео́рия приня́тия реше́ний в усло́виях ри́ска в экономике, теория, которая описывает принципы принятия экономических решений в ситуациях, имеющих более одного исхода с соответствующими вероятностями их наступления. В условиях риска рационально действующий экономический субъект максимизирует функцию ожидаемой полезности (функцию Неймана – Моргенштерна). Результат выбора зависит от несклонности, склонности или нейтрального отношения индивида к риску.

Понятие риска

Понятие риска определил американский экономист Ф. Найт. В работе 1921 г. «Риск, неопределённость и прибыль» учёный привёл следующее утверждение: «…когда речь идёт о риске, распределение исходов в группе случаев известно либо благодаря априорным расчётам, либо из статистических данных прошлого опыта…» (Найт. 2003. С. 225). Таким образом, условия риска, во-первых, предполагают наличие нескольких исходов (случайных событий или состояний природы) – возможных последствий какого-либо действия. Во-вторых, каждому исходу приписывается объективная вероятность его наступления – априорная или статистическая. Априорная вероятность – «классификация абсолютно однородных случаев, идентичных во всех отношениях», а статистическая вероятность – «эмпирическая оценка частоты связей между предиктами» (Найт. 2003. С. 218). В качестве примера, иллюстрирующего различие между этими двумя видами вероятности, Найт приводит азартную игру с бросанием идеальной игральной кости и пожар, в результате которого может сгореть конкретный дом. «Ясно, что вероятность выпадания грани « "шесть" » при бросании кости « "в действительности" » равна одной шестой независимо от того, что происходит при любом конкретном числе бросаний; но никто не станет с уверенностью утверждать, что вероятность возникновения пожара в данном конкретном доме в данный конкретный день "действительно" можно выразить каким-то определённым числовым значением. Первое утверждение интуитивно достоверно применительно к конкретному случаю; второе же – просто эмпирическое обобщение на основе группы событий» (Найт. 2003. С. 210–211).

Определив риск через объективную вероятность, Найт тем самым противопоставил риск неопределённости, которую он предложил связать с субъективной вероятностью, зависящей от веры человека в то, что те или иные события могут произойти. Однако получившая развитие в 1950–1960-е гг. «теория субъективной вероятности лишает такое разграничение смысла, сводя всю неопределённость к риску с помощью ожиданий, выраженных в вероятностях» (Мас-Колелл. 2016. Кн. 1. С. 274).

Предпосылки и аксиомы теории принятия решений в условиях риска

Теория принятия решений в условиях риска основана на следующих предпосылках:

• возможно наступление одного из множества исходов, но какого именно, заранее определить невозможно;

• исходы могут иметь вид наборов благ или денежных сумм;

• множество исходов конечно;

• вероятности всех исходов известны;

• объектами выбора индивида являются лотереи (применяются как формальный способ представления рисковых альтернатив);

• индивид имеет рациональные предпочтения на множестве лотерей.

Простая лотерея сопоставляет вероятность $α_i$ каждому исходу $х_i$ из множества $Х={х_1,…,х_i}$, где $α_i \in [0,1]$ и $\sum_i \alpha_i=1$.

Лотерея, в которой исходы сами являются лотереями, называется сложной (например, когда в лотереях в качестве выигрыша выдаются билеты следующей лотереи).

Пусть $G$ – множество всех лотерей (простых и сложных, но для упрощения бесконечно вложенные сложные лотереи исключены).

Тогда аксиомы выбора в условиях риска можно сформулировать следующим образом:

1. Полнота: для любых двух лотерей $g$ и $g’$ из множества $G$ либо $g≿g’$, либо $g’≿g$ (знак «$≿$» используется для обозначения отношения нестрогого предпочтения, знаки «$\sim$» и «$\succ$» могут использоваться для обозначения отношений безразличия и строгого предпочтения).

2. Транзитивность: для любых трёх лотерей $g$, $g’$ и $g’’$ из $G$, если $g≿g’$ и $g’≿g’’$, то $g≿g’’$.

На основе аксиом полноты и транзитивности можно заключить, что элементы $Х$ упорядочены так, что $х_1≿х_2≿ … ≿х_n$.

3. Непрерывность: если для любой лотереи $g$ из $G$ отношение безразличия не имеет места при крайних значениях $α$ (т. е. при $α=0$ или $α=1$), то оно должно выполняться для некоторого промежуточного значения $α \in [0,1]$, т. е. $g \sim (αx_1, (1-α)x_n)$.

4. Монотонность: если каждая из простых лотерей потенциально приводит только к наилучшему ($x_1$) и наихудшему ($x_n$) исходам, то предпочтительной является та из них, которая приводит к наилучшему исходу с большей вероятностью. Соответственно, для всех вероятностей $α,β \in [0,1]$ отношение предпочтения $(αx_1, (1-α)x_n) ≿ (βx_1, (1-β)x_n)$ будет иметь место тогда и только тогда, когда $α>β$.

5. Замещение: две лотереи эквивалентны для индивида, если для него эквивалентны их исходы и эти исходы реализуются с одинаковыми вероятностями. Иначе: если $g=(α_1g_1, …, α_ng_n)$ и $h=(α_1h_1, …, α_nh_n)$ принадлежат $G$ и $h_i \sim g_i$ для каждого $i$, то $h \sim g$.

6. Сведение к простым лотереям: сложная и порождаемая ею простая лотереи эквивалентны. Например, сложная лотерея, которая с вероятностью $α$ приводит к исходу $x_1$, а с вероятностью $(1-α)$ даёт лотерейный билет, который является простой лотереей и приводит к исходу $x_1$ с вероятностью $β$ и к исходу $x_2$ с вероятностью $(1-β)$, эквивалентна простой лотерее $((α+(1-α)β)x_1, (1-α)(1-β)x_2)$.

7. Независимость: при любых $g$, $g’$ и $g’’$ из $G$ и любых $α \in [0,1]$ отношение предпочтения $g≿g’$ имеет место тогда и только тогда, когда $αg+(1-α)g’’≿αg’+(1-α)g’’$. Иными словами, если каждую из двух лотерей смешать с третьей, то порядок предпочтения этих смешанных лотерей будет таким же, как и для исходных.

Аксиома независимости занимает центральное место в теории выбора в условиях риска, отражая фундаментальный смысл этой теории: индивид не «потребляет» лотерею $g$ или $g’$ вместе с лотереей $g’’$, поэтому его предпочтения в отношении $g$ и $g’$ не зависят от отношения к $g’’$.

Функция ожидаемой полезности

Перечисленные аксиомы позволяют представить предпочтения индивида с помощью функции ожидаемой полезности.

Функция полезности $Eu: G→ R$ (где $R$ – множество исходов всех лотерей из G) обладает свойством ожидаемой полезности, если любой лотерее $g \in G$ соответствует следующее выражение:

$$Eu(g)= \sum_{i=1}^n \alpha_iu(x_i),$$где $(α_i \circ x_i,…,α_n \circ x_n)$ – простая лотерея, порождённая $g$; $u(x_i)$ – полезность исхода $x_i$, которой приписывается $α_i$ – вероятность её получения.

Таким образом, функция ожидаемой полезности сопоставляет каждой лотерее ожидаемое значение полезности, которое она может дать.

Линейная по вероятностям функция, обладающая свойством ожидаемой полезности, названа функцией полезности фон Неймана – Моргенштерна в честь Дж. фон Неймана и О. Моргенштерна, предложивших эту функцию в книге «Теория игр и экономическое поведение» (1944).

Если предпочтения индивида представимы функцией полезности, обладающей свойством ожидаемой полезности, то он отдаст предпочтение одной лотерее перед другой тогда и только тогда, когда ожидаемая полезность одной превосходит ожидаемую полезность другой.

Следовательно, в условиях риска рациональный экономический субъект максимизирует функцию ожидаемой полезности.

Конкретный вид функции ожидаемой полезности зависит от отношения экономического субъекта к риску.

Денежные лотереи и отношение к риску

Пусть выполняется ряд утверждений:

• множество исходов простых денежных лотерей $А$ составляют различные неотрицательные значения денежного дохода: $А=R_+$;

• каждая простая лотерея $g$ имеет вид $(α_i \circ x_i,…,α_n \circ x_n)$, где $α_i≥0$ – вероятности исходов и $\sum_{i=1}^n \alpha_i=1$, $x_i≥0$ – денежные суммы дохода, $n>0$ – целое число;

• функция полезности индивида дифференцируема, и $u' (x)>0$ для всех $x$.

Таким образом, функция ожидаемой полезности $Eu( \cdot )$ определена на лотереях, а функция полезности $u( \cdot )$ – на денежных суммах.

Тогда, если в результате лотереи $g$ сумму денег $x_i$ индивид может получить с вероятностью $α_i$, его ожидаемый доход равен:

$$E(g)= \sum_{i=1}^n \alpha_i{x_i}.$$Если у индивида также есть возможность гарантированно получить ожидаемый доход, то оценки полезностей двух имеющихся у него альтернатив будут следующими:

$$Eu(g)= \sum_{i=1}^n \alpha_iu(x_i),$$$$u(E(g))= u(\sum_{i=1}^n \alpha_i{x_i}),$$где $Eu(g)$ – ожидаемая полезность в случае участия в лотерее; $u(Е(g))$ – полезность ожидаемого дохода в случае его гарантированного получения.

Индивида называют несклонным к риску относительно лотереи $g$, если $u(E(g))>Eu(g)$; склонным к риску относительно лотереи $g$, если $u(E(g))<Eu(g)$; нейтральным к риску относительно лотереи $g$, если $u(E(g))=Eu(g)$.

Если вышеприведённые условия выполняются для любой невырожденной (приписывающей положительные вероятности хотя бы двум различным уровням дохода) простой лотереи $g$, то индивид считается несклонным, склонным или нейтральным к риску на всём пространстве лотерей $G$.

Теорию отношения к риску разработали экономист М. Фридмен и математик Л. Сэвидж в статье 1948 г. «Анализ полезности при выборе среди альтернатив, предполагающих риск». Без проведения эмпирического исследования американские учёные дополнили теорию принятия решений формализацией выбора в условиях риска на основе распространённых наблюдений.

«Люди часто должны или могут выбирать среди альтернатив, отличающихся, помимо прочего, степенью риска, которому человек будет подвержен. Наиболее яркие примеры дают страхование и азартные игры. Человек, страхующий свой дом от пожара, соглашается с определённой потерей небольшой суммы денег (страхового взноса) в предпочтении перед комбинацией малой вероятности гораздо большей потери (стоимости дома) и большей вероятности обойтись без потерь. То есть он выбирает определённость в предпочтении перед неопределённостью» (Фридмен. 2000. С. 208). Такой выбор присущ несклонным к риску индивидам.

«Человек, покупающий лотерейный билет, подвергает себя большей вероятности потери небольшой суммы денег (цены лотерейного билета) и малой вероятности выигрыша большой суммы денег (приза) в предпочтении перед избеганием обоих рисков. Он выбирает неопределённость в предпочтении перед определённостью» (Фридмен. 2000. С. 208). Такие решения свойственны склонным к риску индивидам.

Многие люди «покупают, или хотят покупать, и страховки, и лотерейные билеты» (Фридмен. 2000. С. 232). Они представляют нейтральных к риску индивидов.

Наблюдаемое отношение индивидов к риску формализуется в конкретных свойствах функции полезности.

Функция полезности индивида с любым отношением к риску $u(x)$ является возрастающей, т. е. предельная полезность дохода будет больше нуля при любом его положительном уровне: $u' (x)>0$.

Возможные значения функции ожидаемой полезности расположены на отрезке $АВ$, где точка $А$ соответствует полезности, получаемой индивидом от дохода $x_1$, а точка $В$ – от дохода $x_2$. Абсцисса точки $С$ – это значение ожидаемого дохода $Е(g)$, а её ордината – величина ожидаемой полезности $Eu(g)$ (рис. 1–3).

Функция полезности несклонного к риску индивида имеет вид строго вогнутой кривой (рис. 1). Предельная полезность дохода для такого индивида убывает с ростом $x$, т. е. $u'' (x)<0$. Неравенство Йенсена (обобщающее определение: функция является вогнутой, если для любой пары точек на её графике соединяющая их хорда лежит ниже графика) имеет следующий вид:

$$Eu(g)<u(E(g)),$$или

$$αu(x_1)+(1-α)u(x_2)<u(αx_1+(1-α)x_2).$$Для несклонного к риску индивида значение функции ожидаемой полезности $Eu(g)$ ниже величины полезности $u(E(g))$, которую ему может принести эквивалент его ожидаемого дохода. Именно поэтому несклонный к риску индивид предпочитает определённость.

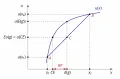Рис. 1. Общий вид функции полезности и функции ожидаемой полезности индивида, несклонного к риску.Рис. 1. Общий вид функции полезности и функции ожидаемой полезности индивида, несклонного к риску.При этом за гарантию отсутствия риска несклонный к риску индивид будет готов лишиться суммы $Е(g)-CE$, где $СЕ$ – гарантированный эквивалент данной лотереи (от англ. certainty equivalent).

Гарантированный эквивалент любой простой денежной лотереи $g$ – это такая сумма денег $CE$, полученная с определённостью, которая приносит индивиду ту же полезность, что и данная лотерея, т. е. $Eu(g) \equiv u(CE)$.

В этом случае денежная сумма $RP$ (от англ. risk premium), выраженная как $RP=Е(g)-CE$, выступает премией за риск (или «платой за избежание риска»).

Таким образом, премия за риск представляет собой такую сумму денег $RP$, при которой выполняется следующее равенство:

$$Eu(g)=u(Е(g)-RP).$$Данную сумму несклонный к риску индивид готов «заплатить», чтобы избежать связанного с лотереей риска.

Если индивид склонен к риску, то его функция полезности является строго выпуклой (рис. 2). Предельная полезность дохода для такого индивида возрастает с ростом $x$, т. е. $u''(x)>0$. Неравенство Йенсена имеет вид:

$$Eu(g)>u(E(g)),$$или

$$αu(x_1)+(1-α)u(x_2)>u(αx_1+(1-α)x_2).$$Для склонного к риску индивида значение функции ожидаемой полезности $Eu(g)$ будет больше, чем величина полезности эквивалента его ожидаемого дохода $u(E(g))$. Именно по этой причине склонный к риску индивид предпочтёт ситуацию риска возможности получения дохода в ситуации определённости. Его денежный эквивалент меры предпочтения неопределённости можно определить как разность $CE-E(g)$.

Рис. 2. Общий вид функции полезности и функции ожидаемой полезности индивида, склонного к риску.Рис. 2. Общий вид функции полезности и функции ожидаемой полезности индивида, склонного к риску.Функция полезности нейтрального к риску индивида – линейная (выпуклая и вогнутая одновременно) функция с положительным наклоном (рис. 3). Предельная полезность дохода не изменяется с ростом x, т. е. $u'' (x)=0$. Равенство Йенсена (обобщающее определение: функция является выпуклой, если для любой пары точек на её графике соединяющая их хорда лежит выше графика) выглядит следующим образом:

$$Eu(g)=u(E(g)),$$или

$$αu(x_1)+(1-α)u(x_2)=u(αx_1+(1-α)x_2).$$Для такого индивида значения функции ожидаемой полезности в каждой точке совпадают с соответствующими значениями функции полезности для эквивалента ожидаемого дохода и гарантированного эквивалента лотереи. «Поэтому безразличный к риску индивид не отдаёт предпочтения ни ситуации риска, ни возможности получения гарантированного дохода, не видя между ними разницы» (Экономическая теория ... 2014. С. 478).

Рис. 3. Общий вид функции полезности и функции ожидаемой полезности индивида, нейтрального к риску.Рис. 3. Общий вид функции полезности и функции ожидаемой полезности индивида, нейтрального к риску.Локально оценивать и сравнивать отношение различных экономических субъектов к риску позволяют специальные показатели, описывающие отношение индивида к риску, называемые мерами Эрроу – Пратта.