Вы́пуклость и во́гнутость фу́нкции, свойство, заключающееся в том, что каждая дуга кривой, являющейся графиком функции $y=f(x)$ на некотором промежутке, лежит не выше или не ниже своей хорды. В случае когда каждая дуга кривой 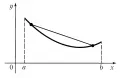Рис. 1. График выпуклой функции.Рис. 1. График выпуклой функции.лежит не выше своей хорды, функцию $f$ называют выпуклой (рис. 1), а в случае когда каждая дуга кривой лежит не ниже своей хорды, – вогнутой (рис. 2) на соответствующем промежутке. Используют и другую терминологию: когда выпуклые функции называют выпуклыми вниз, а вогнутые функции – выпуклыми вверх.

Если функция $f(x)$ выпукла на отрезке $[a, b]$ или на интервале $(a, b)$, то в каждой точке $x∈(a, b)$ она непрерывна и имеет односторонние производные справа и

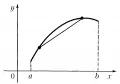Рис. 2. График вогнутой функции.Рис. 2. График вогнутой функции. слева. Каждая из этих производных является возрастающей функцией. Поэтому выпуклая функция имеет производную на интервале $(a, b)$ всюду, за исключением, может быть, конечного или счётного множества точек. Если на интервале $(a, b)$ функция $f(x)$ имеет вторую производную, то $f(x)$ выпукла тогда и только тогда, когда $f″(x)⩾0$. В каждой точке графика выпуклой функции можно провести опорную прямую, т. е. такую прямую, что все точки графика функции лежат на самой прямой или выше неё.

Вогнутость функции $f(x)$ равносильна выпуклости функции $–f(x)$.

Рассматривается выпуклость и вогнутость функций многих переменных. Выпуклость дважды дифференцируемой функции в области равносильна постоянству знака её второго дифференциала в этой области.