Ме́ры Э́рроу – Пра́тта (меры отношения индивида к риску), показатели, позволяющие локально оценить и сравнить отношение экономических субъектов к риску.

Идея измерения отношения индивида к риску была предложена лауреатом Премии памяти А. Нобеля по экономическим наукам 1972 г., американским экономистом К. Дж. Эрроу в начале 1960-х гг. В 1964 г. американский математик и статистик Дж. Пратт (род. 1931) преобразовал эту идею в базовый инструментарий (Pratt. 1964). В 1965 г. Эрроу популяризировал этот инструментарий в курсе лекций «Аспекты теории преодоления риска» (Arrow. 1965), а в 1971 г. опубликовал обширное исследование «Очерки теории преодоления риска» (Arrow. 1971).

Показатели индивидуального отношения к риску получили название «меры Эрроу – Пратта».

В зависимости от отношения к риску индивиды условно разделяются на три типа: расположенные к риску, не расположенные к риску и нейтрально относящиеся к риску. Меры Эрроу – Пратта позволяют оценить и сравнить склонность или несклонность к риску отдельных экономических субъектов. Различают абсолютную и относительную меры Эрроу – Пратта. 

Абсолютная мера Эрроу – Пратта

Пусть $u(x)$ – индивидуальная функция полезности индивида, где $x$ – доход, который может быть потрачен на блага для удовлетворения его потребностей.

Абсолютная мера Эрроу – Пратта, $r(x)$, равна взятому с отрицательным знаком отношению 2-й производной функции полезности к её первой производной, или взятому с обратным знаком отношению скорости убывания предельной полезности дохода к самой предельной полезности:

$$r(x) = -\frac{u''(x)}{u'(x)}. \tag{1}$$Как отмечает Пратт, $r(x)$ можно интерпретировать как меру локального неприятия риска или локальной склонности к страхованию от него (Pratt. 1964. P. 126) при доходе $x$ и функции полезности $u(x)$.

Относительная мера Эрроу – Пратта

Относительная мера Эрроу – Пратта, $r^{ \ast } (x)$, равна эластичности предельной полезности по доходу, взятой с обратным знаком:

$$r^{*}(x)=-\frac{du'(x)}{dx} \cdot \frac{x}{u'(x)}=-\frac{u''(x)}{u'(x)} \cdot x=r(x) \cdot x.\tag{2}$$Показатель $r^{ \ast } (x)$ интерпретируется как мера локального пропорционального неприятия риска (Pratt. 1964. P. 134), отражающая локальное неприятие риска относительно дохода $x$ при функции полезности $u(x)$. Таким образом, относительная мера Эрроу – Пратта даёт представление об отношении индивида к рисковым проектам пропорционально его доходу.

Свойства абсолютной и относительной мер Эрроу – Пратта

Абсолютная и относительная меры Эрроу – Пратта принимают положительные значения для экономических субъектов, не склонных к риску, поскольку функция полезности таких индивидов имеет вид вогнутой кривой (рисунок 1). Предельная полезность дохода для них положительна, но убывает с ростом дохода, т. е. вторая производная функции полезности по доходу меньше 0. Чем большее положительное значение принимает мера Эрроу – Пратта, тем сильнее степень неприятия риска индивидом.

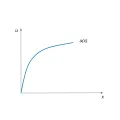Рис. 1. Общий вид функции полезности индивида, не склонного к риску.Рис. 1. Общий вид функции полезности индивида, не склонного к риску.Пример функции полезности и мер Эрроу – Пратта для не склонного к риску индивида:

$$u(x)=ln⁡(x), \tag{3}$$$$r(x) = -\frac{u''(x)}{u'(x)}=-\frac{-\frac{1}{ x^{2}}}{\frac{1}{x}}=\frac{1}{x}, \tag{4}$$$$r^{*}(x)=-\frac{u''(x)}{u'(x)} \cdot x=-\frac{-\frac{1}{ x^{2}}}{\frac{1}{x}} \cdot x=1.\tag{5}$$Если экономический субъект склонен к риску, то абсолютная и относительная меры Эрроу – Пратта для него отрицательны, поскольку его функция полезности имеет вид выпуклой кривой (рисунок 2). Предельная полезность дохода для такого индивида положительна и возрастает с ростом дохода, т. е. вторая производная функции полезности по доходу больше 0.

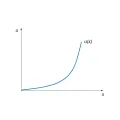Рис. 2. Общий вид функции полезности индивида, склонного к риску.Рис. 2. Общий вид функции полезности индивида, склонного к риску.Пример функции полезности и мер Эрроу – Пратта для склонного к риску индивида:

$$u(x)=x^2,\tag{6}$$$$r(x) = -\frac{u''(x)}{u'(x)}=-\frac{2}{2x}=\frac{1}{x},\tag{7}$$$$r^{*}(x)=-\frac{u''(x)}{u'(x)} \cdot x=-\frac{1}{ x}x=-1.\tag{8}$$Для нейтрального к риску экономического субъекта меры Эрроу – Пратта равны 0, поскольку его функция полезности имеет вид прямой с положительным наклоном (рисунок 3). Предельная полезность дохода для такого индивида положительна и не изменяется с ростом дохода, т. е. вторая производная функции полезности по доходу равна 0.

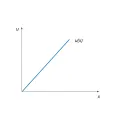Рис. 3. Общий вид функции полезности индивида, нейтрального к риску.Рис. 3. Общий вид функции полезности индивида, нейтрального к риску.Пример функции полезности и мер Эрроу – Пратта для нейтрального к риску индивида:

$$u(x)=x,\tag{9}$$$$r(x) = -\frac{u''(x)}{u'(x)}=0,\tag{10}$$$$r^{*}(x)=-\frac{u''(x)}{u'(x)} \cdot x=0. \tag{11}$$Таким образом, абсолютная и относительная меры Эрроу – Пратта отражают свойства предпочтений индивида.

Преимуществом относительной меры является отсутствие размерности. В частности, если предположить, что доход измеряется в рублях, то, например, для функции полезности $u(x) = ln(x)$ абсолютная мера Эрроу – Пратта $r(x) = -\frac{u''(x)}{u'(x)}=-\frac{-\frac{1}{ x^{2}}}{\frac{1}{x}}=\frac{1}{x}$ имеет размерность 1/руб. Тогда при переходе от измерения дохода в рублях к его измерению в копейках она уменьшится в 100 раз. Безразмерность относительной меры Эрроу – Пратта позволяет избежать подобных трудностей (Экономическая теория. 2014. С. 480). 

Теорема Эрроу – Пратта

Единой меры глобального неприятия риска, которая, например, могла бы отразить более сильное неприятие риска одним индивидом по сравнению с другим, не существует.

Индивида $А$ с функцией полезности $A(x)$ как более не склонного к риску по сравнению с индивидом $В$ с функцией полезности $B(x)$ характеризуют несколько перечисленных далее утверждений, эквивалентность которых для всех значений дохода $x$ обобщает теорема Эрроу – Пратта, или теорема Пратта (Varian. 1992. P. 182–184).

Первое: $r^В(x)<r^А(x)$ для любых $x$.

Второе: $A(x)=φ(B(x))$, где $φ$ – возрастающая строго вогнутая функция, т. е. функция полезности индивида $A$ – это вогнутая трансформация (или вогнутое преобразование) функции полезности индивида $B$, таким образом, функция полезности индивида $A$ «более вогнутая», чем функция полезности индивида $B$ (см. статью Монотонная функция).

Третье утверждение относится к понятию премии за риск как денежной суммы, которую не склонный к риску индивид готов «заплатить», чтобы избежать соответствующего риска: для индивида $А$ эта премия больше, чем для индивида $В$.

В теореме Эрроу – Пратта формулируется эквивалентность всех трёх приведённых выше утверждений.

Иллюстрация теоремы Эрроу – Пратта приведена на рисунке 4, где использованы следующие обозначения:

$\alpha _1$ и $\alpha_2$ – вероятности наступления соответствующих исходов, при которых индивиды могут получить доход величиной либо $x_1$, либо $x_2$;

$Eu_A= \alpha _1u_A(x_1)+ \alpha _2u_A(x_2)$ – значение ожидаемой полезности для индивида $А$, где $u_A(x_1)$ и $u_A(x_2)$ – значения полезности, получаемой этим индивидом при исходах (значениях дохода) $x_1$ и $x_2$;

$Eu_B= \alpha _1u_B(x_1)+ \alpha _2u_B(x_2)$ – значение ожидаемой полезности для индивида $B$, где $u_B(x_1)$ и $u_B(x_2)$ – значения полезности, получаемой этим индивидом при исходах (значениях дохода) $x_1$ и $x_2$;

$Ex= \alpha _1x_1+ \alpha _2x_2$ – ожидаемый доход;

$СЕ_A$ – сумма денег, которая приносит индивиду $А$ полезность, равную её ожидаемому значению;

$СЕ_B$ – сумма денег, которая приносит индивиду $B$ полезность, равную её ожидаемому значению;

$RP_A$ – премия за риск для индивида $А$;

$RP_B$ – премия за риск для индивида $В$.

Рис. 4. Иллюстрация теоремы Эрроу – Пратта.Рис. 4. Иллюстрация теоремы Эрроу – Пратта.

Использование мер Эрроу – Пратта в экономическом анализе

Показатель $r(x)$ использовался Эрроу при анализе оптимальной величины инвестиций, когда часть активов из суммы $x$ должна храниться в виде наличных денег, а остальное инвестируется с определённой строго положительной ожидаемой доходностью.

Если $\tau$ – это доход на единицу вложенных средств, то инвестирование суммы $a$ приведет к получению актива в размере $x+a \tau .$ Тогда, если предположить, что $a(x, \tau )$ является оптимальной суммой для инвестиций, т. е. $a(x, \tau )$ максимизирует ожидаемую полезность $E \{ u(x+a \tau ) \}$, то можно доказать, что при (строго) убывающей, возрастающей или постоянной $r(x)$ соответственно $a(x, \tau )$ (строго) возрастает, убывает или постоянна для всех $x$, за исключением случая, когда $a(x, \tau )=x$ (Pratt, 1964. P. 135).

Эрроу также доказывает теорему об эластичности спроса на наличные по инвестиционным активам, которая эквивалентна утверждению, что если $r^{ \ast } (x)$ (строго) убывает, возрастает или постоянна для всех $x$, то оптимальная доля для инвестиций $a^{*}(x, \tau )=\frac{a(x, \tau )}{x}$ является (строго) возрастающей, убывающей или постоянной соответственно, за исключением случая, когда $a^{*}(x, \tau )=1$ (Pratt. 1964. P. 135).

Относительная мера Эрроу – Пратта представляет собой более общую характеристику отношения индивида к риску, поэтому, например, функции полезности, характеризующейся убывающей абсолютной несклонностью к риску, может соответствовать возрастающая или убывающая относительная несклонность к риску или ни та и ни другая (Pratt. 1964. P. 135).

Пример функции полезности с убывающими абсолютной и относительной несклонностью к риску:

$$u(x)=\sqrt{x-c}, c>0, c=const, x>c;\tag{12}$$$$r(x)=\frac{1}{2(x-c)} >0 – убывает, т. к. r'(x)=-\frac{1}{2{(x-c)}^{2}}<0;\tag{13}$$$$r^* (x)=\frac{x}{2(x-c)} >0 – убывает, т. к. (r^* (x))'=-\frac{c}{2{(x-c)}^2}<0. \tag{14}$$Пример функции полезности с убывающими абсолютной и постоянной относительной несклонностью к риску:

$$u(x)=\sqrt{x}; \tag{15}$$$$r(x)=\frac{1}{2x}>0 – убывает, т. к. r'(x)=-\frac{1}{2{x^2}}<0; \tag{16}$$$$r^*(x)=\frac{1}{2}>0 – постоянна, т. к. (r^*(x))'=0.\tag{17}$$Пример функции полезности с убывающими абсолютной и возрастающей относительной несклонностью к риску:

$$u(x)=\sqrt{x+c}, c>0, c=const, x>c;\tag{18}$$$$r(x)=\frac{1}{2(x+c)} >0 – убывает, т. к. r'(x)=-\frac{1}{2{(x+c)}^{2}}<0;\tag{19}$$$$r^* (x)=\frac{x}{2(x+c)} >0 – возрастает, т. к. (r^* (x))'=\frac{c}{2{(x+c)}^2}>0. \tag{20}$$Однако, если предпочтения индивида характеризуются убывающей относительной несклонностью к риску, наблюдается и убывающая абсолютная несклонность к риску. Это доказывается следующим образом. Поскольку $r^* (x)=r(x)\cdot x$, если относительная несклонность к риску убывает, имеем: $(r^{*}(x))'<0$, или $(r(x))'\cdot x+r(x)<0$. Для не склонного к риску индивида $r(x)>0$. Следовательно, при $x>0$ для выполнения неравенства $(r(x))'\cdot x+r(x)<0$ должно быть $(r(x))'<0$. Соответственно, если относительная несклонность к риску убывает, то убывает и абсолютная несклонность к риску, что и требовалось доказать (Антипина. 2022. С. 110). 

Функции полезности с постоянными абсолютной или относительной мерами Эрроу – Пратта

Функция полезности с постоянной абсолютной мерой

В различных областях экономической науки часто используются функции полезности, характеризующиеся постоянством абсолютной либо относительной меры Эрроу – Пратта.

Функция полезности, для которой абсолютная мера Эрроу – Пратта остается постоянной величиной независимо от величины дохода индивида (constant absolute risk aversion, CARA), определяется следующим дифференциальным уравнением:

$$-\frac{U''(x)}{U'(x)}= \rho =const. \tag{21}$$Степень уравнения (21) можно понизить путём введения вспомогательной функции $U'(x)=y(x)$: $-\frac{\frac{dy}{dx}}{y}= \rho$. Разделяя переменные $\frac{dy}{y}= -\rho dx$, можно интегрировать полученное уравнение: $∫d \ln |y|=- \rho ∫dx$, т. е. $\ln |y|=- \rho x+ \ln c_{1}$, где $\ln c_{1}$ – константа интегрирования; а затем потенцировать полученное решение: $y= c_{1} e^{- \rho x }$. Возвращаясь к исходной функции полезности $\frac{dU}{dx}= c_{1} e^{- \rho x }$, можно решить соответствующее дифференциальное уравнение: $dU= -\frac{c_{1}}{ \rho} de^{- \rho x }$. Интегрирование этого уравнения позволяет получить общий вид функции CARA:

$$U(x)=-\frac{c_1}{ρ}e^{- \rho x}+c_2. \tag{22}$$Введение предпосылки об отсутствии «рога изобилия» (если индивид не имеет дохода, который может быть потрачен на блага для удовлетворения потребностей, то он не получает полезности, т. е. $U(x)=0$ при $x=0$) к функции полезности (22) позволяет получить соотношение между константами $\frac{c_{1}}{ \rho}= c_{2}$. Без ограничения общности (предполагающего, что из любых значений переменных при помощи некоторых преобразований или переименования переменных можно получить исходное выражение с требуемым ограничением на переменные) можно предположить, что $c_{2} =1$, тогда в традиционном виде функция CARA будет выглядеть следующим образом:

$$U(x)=1-e^{-\rho x} . \tag{23}$$

Функция полезности с постоянной относительной мерой

Функция полезности с постоянным относительным неприятием риска (constant relative risk aversion, CRRA) характеризуется постоянством относительной меры Эрроу – Пратта:

$$-\frac{u''(x)}{u'(x)} x=θ=const,$$или $$u''(x) x=-θu'(x).\tag{24}$$Введение обозначения $u'(x) \equiv y$ позволяет понизить степень данного уравнения:

$$\frac{dy}{y}=-θ \frac{dx}{x}.\tag{25}$$Логарифмическая производная $d \ln |y|=-θd \ln |x|$, интегрирование и возврат к исходной переменной позволяют получить линейное однородное дифференциальное уравнение первого порядка:

$$\frac{du}{dx}= c_{1}x^{ -θ}.\tag{26}$$При $\theta \neq 1$ уравнение (26) переписывается следующим образом:

$$du= c_{1}x^{-θ} dx=\frac{c_{1}}{(1-θ)}dx^{1-θ} , θ≠1.\tag{27}$$Результатом интегрирования уравнения (27) является уравнение (28):

$$u(x)=\frac{c_{1}x^{1-θ}}{1-θ}+c_{2}, θ≠1.\tag{28}$$При константах интегрирования $c_{1} =1$ и $c_{2} =-\frac{1}{1-θ}$ элементарная функция полезности (Бернулли) с постоянным относительным неприятием риска ($\theta \neq 1$) будет иметь следующую форму:

$$u(x)=\frac{x^{1-θ}-1}{1-θ}.\tag{29}$$При $\theta=1$ и $c_{1} =1$ линейное однородное дифференциальное уравнение первого порядка (26), характеризующее функцию CRRA, принимает вид (30):

$$\frac{du}{dx}=\frac{1}{x},$$или $$du=\frac{dx}{x}=d \ln ⁡x.\tag{30}$$Решением уравнения (30) является логарифмическая функция полезности $u= \ln x+c_{2}$. Константу $c_{2}$ без ограничения общности можно считать нулевой: $u= \ln x$. Данный случай является предельным для предыдущего ($\theta \neq 1$) при $\theta \rightarrow 1$. Полагая $\sigma =1- \theta$ и применяя правило Лопиталя, можно получить уравнение (31):

$$\lim_{θ \rightarrow 1}\frac{x^{1-θ}-1}{1-θ}= \lim_{ \sigma \rightarrow 0}\frac{x^{ \sigma }-1}{ \sigma}=\lim_{ \sigma \rightarrow 0}\frac{x^{ \sigma } \ln x}{ 1}=\ln ⁡x. \tag{31}$$Рассмотрим аддитивную межвременную функцию полезности, построенную на базе динамической функции CRRA вида $U_t=\frac{x_t^{1-θ}-1}{1-θ}$:

$$u= \sum_{t=0}^ \infty \frac{u_{t}}{ (1+ \rho )^{t}} = \sum_{t=0}^ \infty \frac{( x_t^{1- \theta}-1)}{ (1- \theta )(1+ \rho )^{t}},\tag{32}$$где $0< ρ <1$ – норма межвременных предпочтений.

Предельная норма межвременного замещения для данной функции будет иметь вид (33):

$$MRS_{t,t+1}=-\frac{dx_{t+1}}{dx_t}=\frac{MU_t}{MU_{t+1}} =(1+ρ) (\frac{x_t}{x_{t+1}} )^{-θ}=(1+ρ) (\frac{x_{t+1}}{x_t})^{θ}. \tag{33}$$Из уравнения (33) следует, что $\frac{x_{t+1}}{x_t} =\frac{MRS_{t,t+1}^{\frac{1}{θ}}}{(1+ρ)^{\frac{1}{θ}}}$.

Аддитивная межвременная функция полезности, построенная на базе динамической функции CRRA, характеризуется постоянной межвременной эластичностью замещения (Вереникин. 2022. С. 64–67) вида (34):

$$δ=\frac{d(\frac{x_{t+1}}{x_t}) }{dMRS_{t,t+1}} \frac{MRS_{t,t+1}}{(\frac{x_{t+1}}{x_t})}=\frac{1}{(1+ρ)^{\frac{1}{θ}}} \frac{dMRS_{t,t+1}^{\frac{1}{θ}}}{dMRS_{t,t+1}} \frac{MRS_{t,t+1} (1+ρ)^{\frac{1}{θ}}}{MRS_{t,t+1}^{\frac{1}{θ}}}=\frac{1}{θ}. \tag{34}$$