Геоме́трия Лобаче́вского, одна из неевклидовых геометрий, основана на тех же посылках, что и обычная – евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на иную. Евклидова аксиома о параллельных состоит в том, что через точку, не лежащую на данной прямой, проходит не более чем одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её (в евклидовой геометрии такие прямые называют параллельными). В геометрии Лобачевского эта аксиома заменяется следующей: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (достаточно, чтобы это было выполнено для одной точки и одной прямой). Начало геометрии Лобачевского было положено Н. И. Лобачевским, который впервые сообщил о ней в 1826 г. Несколько позднее эту же теорию предложил Я. Больяй; поэтому геометрию Лобачевского иногда называют геометрией Лобачевского – Больяя. Её также называют неевклидовой геометрией, хотя обычно термину «неевклидова геометрия» придают более широкий смысл, включая сюда и другие теории, возникшие вслед за геометрией Лобачевского, а также теории, основанные на изменении посылок евклидовой геометрии. Геометрию Лобачевского иногда называют гиперболической неевклидовой геометрией в противоположность эллиптической геометрии Римана.

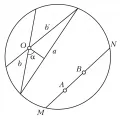Рис. 1. Модель Клейна.Рис. 1. Модель Клейна.С современной точки зрения можно дать, например, следующее определение геометрии Лобачевского на плоскости: геометрия Лобачевского есть геометрия внутри круга на обычной (евклидовой) плоскости, лишь выраженная особым способом. Именно, внутренность круга, т. е. круг за исключением ограничивающей его окружности, называют «плоскостью» (рис. 1). Точкой «плоскости» является точка внутри круга. «Прямой» называют любую хорду (например, $a,b,b',M\!N$ с исключёнными концами (т. к. окружность исключена из «плоскости»); «движением» – любое преобразование круга самого в себя, которое переводит хорды в хорды. Равными называются фигуры внутри круга, которые можно перевести одну в другую такими преобразованиями. Оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь не выполняется, т. к. через точку $O$, не лежащую на данной хорде $a$ (т. е. «прямой»), проходит сколь угодно много не пересекающих её хорд («прямых», напр. $b$ и $b'$). Аналогично геометрия Лобачевского в пространстве может быть определена как геометрия внутри шара, выраженная в соответствующих терминах («прямые» – хорды, «плоскости» – плоские сечения внутренности шара, «равные» фигуры – те, которые переводятся одна в другую преобразованиями, переводящими шар сам в себя и хорды в хорды). Таким образом, геометрия Лобачевского имеет совершенно реальный смысл и столь же непротиворечива, как геометрия Евклида.

Исторический очерк

Возникновение геометрии Лобачевского связано с вопросом об аксиоме о параллельных, которая известна также как V постулат Евклида (под этим номером утверждение, эквивалентное приведённой выше аксиоме о параллельных, фигурирует в списке постулатов в «Началах» Евклида). Этот постулат ввиду его сложности по сравнению с другими вызвал многочисленные попытки его доказательства на основании других постулатов.

Среди учёных, занимавшихся доказательством V постулата до 19 в.: Птолемей, Прокл (его доказательство основано на предположении о конечности расстояния между параллельными), арабский учёный Ибн аль-Хайсам (конец 10 – начало 11 вв.; пытался доказать V постулат, исходя из предположения, что конец движущегося перпендикуляра к прямой описывает прямую линию), Омар Хайям и азербайджанский математик Насир ад-Дин Туси (13 в.) (при доказательстве V постулата исходили из предположения, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения), немецкий учёный Х. Шлюссель (Клавиус, 16 в.); итальянские учёные П. Катальди (в 1603 впервые напечатал работу, целиком посвящённую вопросам о параллельных), Дж. Борелли (1658), Дж. Витали (1680); Дж. Валлис (1663, опубликовано в 1693; основывал доказательство постулата на предположении, что для всякой фигуры существует ей подобная, но не равная фигура). Доказательства вышеперечисленных геометров сводились к замене V постулата другим предположением, казавшимся более очевидным. Итальянский учёный Дж. Саккери (1733) сделал попытку доказать V постулат от противного. Приняв предложение, противоречащее постулату Евклида, Саккери получил из него довольно обширные следствия. Ошибочно признав некоторые из этих следствий приводящими к противоречиям, Саккери заключил, что постулат Евклида доказан. И. Ламберт (около 1766, опубликовано в 1786) предпринял аналогичные исследования, однако он не повторил ошибки Саккери, а признал своё бессилие обнаружить в построенной им системе логическое противоречие. Попытки доказательства постулата предпринимались и в 19 в. Следует отметить работы А.-М. Лежандра; одно из его доказательств (1800) основано на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла, т. е., как и все его предшественники, он заменил V постулат другим допущением. К построению геометрии Лобачевского подошли немецкие учёные Ф. Швейкарт (1818) и Ф. Тауринус (1825).

Вопрос о V постулате Евклида, занимавший геометров более двух тысячелетий, был решён Лобачевским. Решение сводится к тому, что этот постулат не может быть доказан на основе других посылок евклидовой геометрии и что принятие иного постулата позволяет построить геометрию, столь же содержательную, как и евклидова. Хотя геометрия Лобачевского развивалась как умозрительная теория и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно он рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Доказательство её непротиворечивости было дано позднее, когда были указаны её интерпретации.

Интерпретации (модели) геометрии Лобачевского

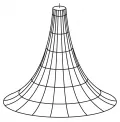Рис. 2. Псевдосфера.Рис. 2. Псевдосфера.Геометрия Лобачевского изучает свойства плоскости Лобачевского в планиметрии и пространства Лобачевского в стереометрии. Плоскость Лобачевского – это плоскость (множество точек), в которой определены прямые линии (а также движения фигур, расстояния, углы и пр.), подчиняющиеся всем аксиомам евклидовой геометрии, за исключением аксиомы о параллельных, которая заменяется сформулированной выше аксиомой Лобачевского. Сходным образом определяется пространство Лобачевского. Задача выяснения реального смысла геометрии Лобачевского состояла в нахождении моделей плоскости и пространства Лобачевского, т. е. в нахождении таких объектов, в которых реализовывались бы соответствующим образом истолкованные положения планиметрии и стереометрии геометрии Лобачевского. В 1868 г. Э. Бельтрами заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера (рис. 2). Если точкам и прямым на конечном куске плоскости Лобачевского сопоставить точки и кратчайшие линии (геодезические) на псевдосфере и движению плоскости Лобачевского сопоставить перемещение фигуры по псевдосфере с изгибанием, т. е. деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. Таким образом, геометрия Лобачевского получает простой реальный смысл (интерпретация Бельтрами). При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере, однако здесь даётся интерпретация только геометрии на куске плоскости Лобачевского, а не на всей плоскости и тем более не в пространстве. В 1901 г. Д. Гильберт доказал, что в евклидовом пространстве не может существовать регулярной поверхности, геометрия на которой совпадает с геометрией всей плоскости Лобачевского.

В 1871 г. Ф. Клейн указал описанную выше модель (интерпретация Клейна) как всей плоскости, так и пространства Лобачевского: плоскостью служит внутренность круга, а пространством – внутренность шара. В этой модели расстояние между точками $A$ и $B$ (рис. 1) определяется как $\displaystyle\ln \left ( \frac{AN}{AM}\cdot \frac{BM}{BN} \right)$. Позднее А. Пуанкаре в связи с задачами теории функций комплексного переменного дал другую модель (интерпретация Пуанкаре). В этой интерпретации за плоскость Лобачевского принимается внутренность круга (рис. 3), прямыми считаются дуги окружностей (например, $a,b,b'$), перпендикулярных окружности данного круга, и его диаметры, движениями – преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми. В модели Пуанкаре углы изображаются обычными углами. Модель геометрии Лобачевского в пространстве строится аналогично.

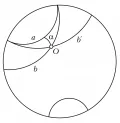Рис. 3. Модель Пуанкаре.Рис. 3. Модель Пуанкаре.Коротко модели Клейна и Пуанкаре можно определить так. В обоих случаях плоскостью Лобачевского может служить внутренность круга (пространством – внутренность шара), и геометрия Лобачевского есть теория о тех свойствах фигур внутри круга (шара), которые в случае модели Клейна не изменяются при проективных, а в случае модели Пуанкаре – при конформных преобразованиях круга (шара) самого в себя (проективные преобразования переводят прямые в прямые, конформные – сохраняют углы).

Возможно чисто аналитическое определение модели геометрии Лобачевского. Например, точки плоскости можно определять как пары чисел $(x,y)$, прямые можно задавать уравнениями, движения – формулами, сопоставляющими точкам $(x,y)$ новые точки $(x' ,y' )$. Это абстрактно определённая аналитическая геометрия на плоскости Лобачевского, аналогичная аналитической геометрии на евклидовой плоскости. Лобачевский дал основы своей аналитической геометрии и тем самым фактически наметил такую модель, хотя полное её построение выяснилось уже после того, как на основе работ Ф. Клейна и др. выявилось само понятие о модели. Другое аналитическое определение геометрии Лобачевского состоит в том, что она определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано Б. Риманом (1854) и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь в 1868 г.

Содержание геометрии Лобачевского

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют т. н. абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрий. Ниже перечислены несколько фактов геометрии Лобачевского, установленных самим Н. И. Лобачевским, которые отличают её от геометрии Евклида.

1. В геометрии Лобачевского не существует подобных, но не равных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами. Таким отрезком может служить, например, сторона правильного треугольника с данной суммой углов.

2. Сумма углов всякого треугольника меньше $\pi$ и может быть сколь угодно близкой к нулю. Это видно на модели Пуанкаре. Разность $π-(α+β+γ)$, где $α ,β ,γ$ – углы треугольника, пропорциональна его площади.

3. Через точку $O$, не лежащую на данной прямой $a$, проходит бесконечно много прямых, не пересекающих $a$ и находящихся с ней в одной плоскости; среди них есть две крайние $b$ и $b'$, которые называются параллельными прямой $a$ в смысле Лобачевского. В моделях Клейна и Пуанкаре они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) $a$ общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек, рис. 1, 3). Угол $α$ между прямой $b$ (или $b'$) и перпендикуляром из $O$ на $a$, т. н. угол параллельности, по мере удаления точки $O$ от прямой $a$ убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно увидеть непосредственно). Параллель $b$ с одной стороны (а $b'$ с противоположной) асимптотически приближается к $a$, а с другой – бесконечно от неё удаляется (в моделях расстояние между точками, приближающимися к разным точкам граничной окружности, бесконечно растёт).

4. Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

5. Линия равных расстояний от прямой есть не прямая, а особая кривая, называемая эквидистантой или гиперциклом.

6. Предел бесконечно растущих окружностей есть не прямая, а особая кривая, называемая предельной окружностью или орициклом.

7. Предел сфер бесконечно увеличивающегося радиуса есть не плоскость, а особая поверхность – предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это послужило Лобачевскому основой для вывода формул тригонометрии.

8. Длина окружности не пропорциональна радиусу, а растёт быстрее, чем радиус.

9. Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше метрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Например, чем меньше треугольник, тем меньше сумма его углов отличается от $\pi$, чем меньше окружность, тем меньше отношение её длины к радиусу отличается от $2\pi$, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

Применение геометрии Лобачевского

Лобачевский применил свою геометрию к вычислению определённых интегралов. В теории функций комплексного переменного геометрия Лобачевского помогла построить теорию автоморфных функций. Связь с геометрией Лобачевского здесь была отправным пунктом исследований Пуанкаре, который писал, что «неевклидова геометрия есть ключ к решению всей задачи». Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединённых под названием геометрия чисел. Установлена связь геометрии Лобачевского с кинематикой частной теории относительности. Эта связь основана на том, что равенство, выражающее закон распространения света $$x^2+y^2+z^2=c^2t^2$$(где $c$ – скорость света, $t$ – время), при делении на $t^2$, т. е. для скоростей, даёт равенство $$v_x^2+v_y^2+v_z^2 = c^2,$$т. е. уравнение сферы в пространстве с координатами $v_x,v_y,v_z$ (в пространстве «скоростей»). Преобразования Лоренца сохраняют эту сферу и, т. к. они линейны, переводят прямые пространства скоростей в прямые. Поэтому, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса $c$, т. е. для скоростей, меньших скорости света (которые, согласно теории относительности, только и возможны), имеет место геометрия Лобачевского. Так, например, сложение скоростей в теории относительности получает истолкование как сложение отрезков в геометрии Лобачевского.

Геометрия Лобачевского нашла применение в общей теории относительности. Если считать распределение масс материи во Вселенной равномерным, что в космических масштабах представляет допустимое приближение, то оказывается, что пространство имеет геометрию Лобачевского. Таким образом, оправдалось предположение Лобачевского о его геометрии как возможной теории реального пространства.