Кривизна́, величина, характеризующая отклонение кривой (поверхности) от прямой (плоскости). Отклонение дуги $MM \prime$ кривой $L$ от касательной $MT$ в точке $M$ (см. рисунок) можно охарактеризовать с помощью т. н. средней кривизны $k_{cp}$ этой дуги, равной отношению $α/Δs$ величины $α$ угла между касательными в точках $M$ и $M'$ к длине $Δs$ дуги $MM'$.

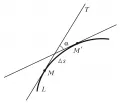Отклонение дуги 𝑀𝑀′ кривой 𝐿 от касательной 𝑀𝑇 в точке 𝑀.Отклонение дуги 𝑀𝑀′ кривой 𝐿 от касательной 𝑀𝑇 в точке 𝑀. Для дуги окружности средняя кривизна в каждой точке равна величине, обратной радиусу этой окружности, и характеризует степень искривлённости окружности: с уменьшением радиуса увеличивается искривлённость дуги. Предельное значение средней кривизны при стремлении точки $M'$ к точке $M$, т. е. при $Δs→ 0,$ называется кривизной $k$ кривой $L$ в точке $M$: $$k=\lim_{M'\to M}k_{ср}=\lim_{\Delta s \to 0}\frac {\alpha}{\Delta s}.$$Величину $R=1/k$, обратную кривизне, обычно называют радиусом кривизны кривой $L$ в точке $M$.

Если кривая $L$ является графиком функции $у=f(x)$, то кривизна $k$ этой кривой в точке $x$ может быть вычислена по формуле $$k=\frac{|f''(x)|}{(1+f'^2(x))^{3/2}}.$$Кривизна $k$ кривой $L$ представляет собой, вообще говоря, функцию длины дуги $s$, отсчитываемой от некоторой точки $M$ этой кривой. Если для двух плоских кривых $L_1$ и $L_2$ кривизны как функции длины дуги одинаковы, то кривые $L_1$ и $L_2$ конгруэнтны, т. е. они могут быть совмещены движением. Уравнение, задающее кривизну $k$ как функцию длины дуги, обычно называется натуральным уравнением этой кривой.

Для характеристики отклонения пространственной кривой $L$ от плоскости вводят понятие кручения. Кривизна и кручение, заданные как функции длины дуги, определяют кривую $L$ с точностью до положения в пространстве.

Описание отклонения поверхности от плоскости может быть проведено следующим образом. Через нормаль в данной точке $M$ поверхности проводят всевозможные плоскости. Сечения поверхности этими плоскостями называют нормальными сечениями, а кривизну нормальных сечений в точке $M$ – нормальными кривизнами поверхности в этой точке. Максимальная и минимальная из нормальных кривизн в данной точке $M$ называются главными кривизнами. Величины $K=k_1k_2$ и $Н=(k_1+k_2)/2$, где $k_1$ и $k_2$ – главные кривизны, называются соответственно гауссовой кривизной и средней кривизной поверхности в точке $M$. Эти кривизны поверхности определяют нормальные кривизны, поэтому они могут служить характеристиками отклонения поверхности от плоскости. В частности, если $K=0$ и $H=0$ во всех точках поверхности, то она является плоскостью.

Гауссова кривизна не меняется при изгибаниях поверхности. Если, например, гауссова кривизна равна нулю во всех точках поверхности, то каждый достаточно малый её кусок может быть изгибанием сделан плоским. Гауссова кривизна на поверхности без обращения к объемлющему пространству составляет объект т. н. внутренней геометрии поверхности. Средняя кривизна связана с внешней формой поверхности.

Понятие кривизны обобщается на объекты более общей природы. Например, оно возникает в т. н. римановых пространствах, представляя собой меру отклонения этих пространств от евклидовых.