Многообра́зие, многомерное обобщение понятий линии и поверхности без особых точек. Топологическим многообразием размерности $n$ называется топологическое пространство $M$, каждая точка которого обладает окрестностью, гомеоморфной открытому шару $x^2_1+ ...+x^2_n< 1$ $n$-мерного евклидова пространства ${\bf R}^n$. Обычно предполагают также, что $M$ покрывается конечным или счётным числом окрестностей такого рода и что $M$ отделимо, т. е. любые две его точки обладают непересекающимися окрестностями.

Разнообразные примеры многообразий размерностей $1, 2$ и $3$ встречаются в геометрии. Прямая, открытый интервал, парабола, окружность, эллипс – одномерные многообразия. Любая область на плоскости, сама плоскость, параболоид, сфера, эллипсоид, тор и т. п. – двумерные многообразия. Поверхность конуса не является многообразием, т. к. вершина конуса, в которой сходятся две его полости, не имеет окрестности, гомеоморфной кругу. Обычное трёхмерное евклидово пространство, а также любая область в нём – трёхмерное многообразие.

Введение в математику понятия многообразия любого числа измерений было вызвано весьма разнообразными потребностями геометрии, математического анализа, механики и физики. Это понятие применимо практически во всех ситуациях, когда рассматриваемые объекты могут быть параметризованы системами действительных чисел. Точками возникающих при этом многообразий могут быть объекты любой природы – прямые, сферы, матрицы, состояния механической системы и пр.

Многообразие называется замкнутым, если оно компактно, и открытым в противном случае. Каждое замкнутое многообразие размерности $1$ гомеоморфно окружности, а каждое открытое – прямой (на рис. 1 изображены одномерные многообразия и окрестности точки $P$ на каждом из них).

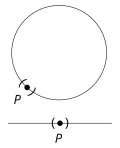Рис. 1. Одномерные многообразия.Рис. 1. Одномерные многообразия.В случае двух измерений уже замкнутые многообразия довольно разнообразны. Они распадаются на бесконечное число топологических типов: сфера – поверхность рода $0$ (рис. 2, а), тор – поверхность рода $1$ (рис. 2, б), «крендель» – поверхность рода $2$ (рис. 2, в), вообще «сфера с $n$ ручками» – поверхность рода $n$ (на рис. 2, г изображена такая поверхность при $n=3$).

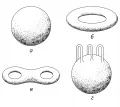Рис. 2. Замкнутые многообразия в случае двух измерений.Рис. 2. Замкнутые многообразия в случае двух измерений.Этими примерами исчерпываются все топологические типы замкнутых двумерных ориентированных многообразий. Существует ещё бесконечное число замкнутых двумерных неориентируемых многообразий – односторонних поверхностей; например, проективная плоскость, поверхность Клейна. Имеется классификация открытых двумерных многообразий. Полная классификация многообразий трёх измерений не найдена (даже для случая замкнутых многообразий).

Определение топологического многообразия не даёт возможности определить дифференцируемые функции и другие понятия математического анализа на многообразии. Чтобы эти понятия приобрели смысл, необходимо ввести на многообразии дополнительную структуру. В окрестности любой точки $n$-мерного топологического многообразия существуют локальные координаты $x_1,...,x_n$, однозначно определяющие положение точки этой окрестности. Если выбрать локальные координаты в окрестности любой точки многообразия таким образом, что две разные системы локальных координат в пересекающихся окрестностях выражаются друг через друга при помощи функций класса $C^k, k⩾1$, то получится гладкая структура класса $k$. Обычно берут $k=∞$ и многообразие с гладкой структурой называют дифференцируемым (или гладким) многообразием. Дифференцируемые многообразия имеют большое значение в современной математике, поскольку именно они наиболее широко используются в приложениях и смежных областях (см. Дифференциальная геометрия). На одном и том же топологическом многообразии могут существовать различные (и даже не изоморфные) гладкие структуры. Аналогично вводится понятие аналитического многообразия. Если считать локальные координаты комплексными числами и потребовать, чтобы они выражались друг через друга при помощи аналитических функций, то получится понятие комплексного (аналитического) многообразия.

Понятие многомерного многообразия впервые сформулировано Б. Риманом в его лекции «О гипотезах, лежащих в основании геометрии» (1854). В 1913 г. Г. Вейль ввёл понятие (абстрактной) римановой поверхности, т. е. одномерного комплексного многообразия (с каждой аналитической функцией комплексного переменного связывается такое многообразие, называемое римановой поверхностью этой функции).

В современной математике рассматриваются также различные обобщения понятия многообразия. Таковы, например, многообразия с краем (типичным примером которых является замкнутый шар $x^2_1+ ...+x^2_n⩽ 1$ в пространстве ${\bf R}^n$), а также аналитические пространства (включающие в себя вещественные или комплексные аналитические поверхности с особыми точками).