Координа́ты (от лат. co – совместно и ordinatus – упорядоченный, определённый), числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Первыми координатами, вошедшими в систематическое употребление, являются астрономические (см. Системы небесных координат) и географические координаты – широта и долгота, определяющие положение точки на небесной сфере или на поверхности земного шара. В 14 в. Николай Орем пользовался координатами на плоскости для построения графиков, называя долготой и широтой то, что ныне называют абсциссой и ординатой. Систематически метод координат, позволяющий переводить задачи геометрии на язык математического анализа и обратно и тем самым геометрически истолковывать факты анализа, начал применять Р. Декарт. Кроме координат точки, рассматривают также координаты прямой, плоскости и других геометрических объектов, считая параметры, однозначно определяющие эти объекты, их координатами. Аналогами координат являются, например, коэффициенты многочлена и коэффициенты ряда Фурье.

На плоскости и в пространстве помимо декартовой системы координат используются полярные координаты на плоскости и сферические координаты в пространстве. 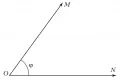Рис. 1. Полярные координаты.Рис. 1. Полярные координаты.Полярные координаты точки на плоскости (рис. 1) получают, выбирая точку $O$ (полюс) и выходящий из неё луч $ON$ (полярную ось). Координатами точки $M$ служат расстояние $ρ=| \overrightarrow {OM}|$ (полярный радиус) и угол $φ = \angle NOM$ (полярный угол). Каждой точке $M$ плоскости соответствует пара чисел $(ρ ,φ)$, где $0⩽ρ<∞$, $0⩽φ< 2π$, эти числа называются полярными координатами точки $M$.

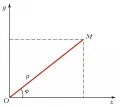Рис. 2. Декартовы и полярные координаты.Рис. 2. Декартовы и полярные координаты.Соответствие между точками $M$, отличными от $O$, и парами $(ρ ,φ )$, подчинёнными указанным условиям, взаимно однозначно. Для точки $O$ величина $ρ=0$, а угол $φ$ не определён.

Если на плоскости используются и декартова прямоугольная, и полярная системы координат такие, что полюс $O$ полярной системы и начало координат $O$ декартовой системы совпадают, а луч $ON$ совпадает с осью $Ox$, то декартовы координаты $(x,y)$ и полярные координаты $(ρ ,φ)$ (рис. 2) связаны равенствами $$x=ρ \cos\,φ,\ \ \ \ y=ρ \cos\,φ.$$Полярные координаты в неявном виде использовал древнегреческий учёный Динострат (4 в. до н. э.). И. Ньютон в «Методе флюксий» (1670–1671) трижды использовал полярные координаты и привёл формулы, связывающие их с прямоугольными координатами. В почти современном виде полярные координаты появились у Я. Бернулли (1691), чёткое представление об определении точки на плоскости при помощи полярных координат имеется у Л. Эйлера (1748).

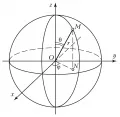Рис. 3. Сферические и декартовы координаты.Рис. 3. Сферические и декартовы координаты.Сферическими координатами точки $M$ в пространстве являются три числа $r, θ ,φ$, которые определяются следующим образом. Через фиксированную точку $O$ проводятся три взаимно перпендикулярные оси $Ox, Oy, Oz$ (рис. 3). Число $r$ равно расстоянию от точки $O$ до точки $M$, $θ$ представляет собой угол между вектором $\overrightarrow{OM}$ и положительным направлением оси $Oz$, $φ$ – угол, на который надо повернуть против часовой стрелки положительную полуось $Ox$ до совпадения с направлением вектора $\overrightarrow{ON}$ ($N$ – проекция точки $M$ на плоскость $xOy$). Сферические координаты точки $M$ зависят от выбора точки $O$ и трёх осей $Ox, Oy, Oz$. Связь сферических координат с прямоугольными декартовыми координатами устанавливается формулами $$x=r \sin θ \cos φ, \ \ \ y=r \sin θ \sin φ, \ \ \ z=r \cos θ.$$Формулы, связывающие сферические координаты с прямоугольными координатами, приведены Ж.-Л. Лагранжем (1773), название «сферические координаты» предложил немецкий учёный Г. Бальтцер (1882).

В случае общих декартовых координат на плоскости линии $x=c, -∞\lt c \lt ∞$, образуют множество прямых, параллельных оси $Oy$, а линии $y=c, -∞\lt c \lt ∞$, – множество прямых, параллельных оси $Ox$; через точку $M$ с декартовыми координатами $(x_0,y_0)$ проходит одна прямая $x=x_0$ из первого множества и одна прямая $y=y_0$ из второго множества. В случае полярных координат линии $ρ=c, c>0$, являются окружностями, а линии $φ=c, 0⩽c<2π$, – лучами, выходящими из начальной точки $O$; через точку $M$ с полярными координатами $(ρ_0,φ_0)$, отличную от $O$, проходит по одной линии $ρ=ρ_0$ и $φ=φ_0$ каждого из двух указанных семейств, эти линии пересекаются в точке $M$. В более общем случае рассматривают в какой-либо области $G$ плоскости две функции точки $u(M)$ и $v(M)$ такие, что каждая линия $u(M)=const$ пересекается с каждой линией семейства $v(M)=const$ в пределах области $G$ в одной точке. В этом случае числа $u(M)$ и $v(M)$ называются криволинейными координатами, они однозначно определяют положение точки $M$ в области $G$, т. е. являются координатами точки $M$ в этой области. В пространстве также пользуются системами криволинейных координат, схема построения которых такова: в какой-либо области $G$ пространства рассматриваются три функции точки $u(M), v(M), w(M)$ такие, что через каждую точку $M$ области $G$ проходит одна поверхность семейства $u=const$, одна поверхность семейства $v=const$ и одна поверхность семейства $w=const$. Тем самым каждой точке $M$ ставятся в соответствие три числа ($u,v,w$) – её координаты в области $G$. Аналогично вводятся криволинейные координаты на поверхности. Например, для случая долготы $φ$ и широты $θ$ на сфере линиями $φ=const$ являются меридианы, а линиями $θ=const$ – параллели. Криволинейные координаты на произвольной поверхности применяются в дифференциальной геометрии. Криволинейные координаты впервые использовал Я. Бернулли (1691), координатами назвал их год спустя Г. В. Лейбниц. С именем К. Ф. Гаусса связаны криволинейные координаты на поверхности. Криволинейные координаты в пространстве и название «криволинейные координаты» ввёл Г. Ламе (1833).