Дифференциа́льное исчисле́ние, раздел математического анализа, в котором изучаются производные, дифференциалы и их применение к исследованию функций. Дифференциальное исчисление сложилось как самостоятельная дисциплина во 2-й половине 17 в. под влиянием трудов И. Ньютона и Г. В. Лейбница, в которых они сформулировали основные положения дифференциального исчисления и отметили взаимно обратный характер дифференцирования и интегрирования. С этого времени дифференциальное исчисление развивалось в тесной связи с интегральным исчислением, составляя вместе с ним основную часть математического анализа (или анализа бесконечно малых). Создание дифференциального и интегрального исчислений открыло новую эпоху в развитии математики, повлекло за собой появление ряда новых математических дисциплин (теории рядов, теории дифференциальных уравнений, дифференциальной геометрии, вариационного исчисления, функционального анализа) и существенно расширило возможности приложений математики к вопросам естествознания и техники.

Дифференциальное исчисление основывается на таких фундаментальных понятиях, как действительное число, функция, предел, непрерывность. Эти понятия приняли современный вид в ходе развития дифференциального и интегрального исчислений. Основные идеи и понятия дифференциального исчисления связаны с изучением функций в малом, т. е. в малых окрестностях отдельных точек, для чего требуется создание математического аппарата для исследования функций, поведение которых в достаточно малой окрестности каждой точки области их определения близко к поведению линейной функции или многочлена. Этот аппарат основан на понятиях производной и дифференциала. Понятие производной возникло в связи с большим числом различных задач естествознания и математики, приводящих к вычислению пределов одного и того же типа. Важнейшие из этих задач – определение скорости движения материальной точки вдоль прямой линии и построение касательной к кривой. Понятие дифференциала связано с возможностью приближения функции в малой окрестности рассматриваемой точки линейной функцией. В отличие от понятия производной функции действительной переменной, понятие дифференциала легко переносится на функции более общей природы, в т. ч. на отображения одного евклидова пространства в другое, на отображения банаховых пространств в другие банаховы пространства, и служит одним из основных понятий функционального анализа.

Производная

Пусть материальная точка движется вдоль оси $Oy$, а $x$ обозначает время, отсчитываемое от некоторого начального момента. Описание этого движения даёт функция $y=f(x)$, ставящая в соответствие каждому моменту времени $x$ координату $y$ движущейся точки. Эту функцию в механике называют законом движения. Важной характеристикой движения (особенно если оно является неравномерным) является скорость движущейся точки в каждый момент времени$$x (эту скорость называют также мгновенной скоростью). Если точка движется по оси $Oy$ по закону $y=f(x)$, то в произвольный момент времени $x$ она имеет координату $f(x)$, а в момент времени $x+Δx$ – координату $f(x+\Delta x)$, где $Δx$ – приращение времени. Число $Δy=f(x+Δx)-f(x)$, называемое приращением функции, представляет собой путь, пройденный движущейся точкой за время от $x$ до $x+Δx$. Отношение

$$\frac{\Delta y}{\Delta x }=\frac{f(x+\Delta x)-f(x)}{\Delta x},\tag 1$$называемое разностным отношением, представляет собой среднюю скорость движения точки в промежутке времени от $x$ до $x+Δx$. Мгновенной скоростью (или просто скоростью) движущейся точки в момент времени x называется предел, к которому стремится средняя скорость (1) при стремлении к нулю промежутка времени $Δx$, т. е. предел

$$\lim_{Δx\to 0}\frac{Δy}{Δx}=\lim_{Δx\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}.\tag2$$Понятие мгновенной скорости приводит к понятию производной. Производной произвольной функции $y=f(x)$ в данной фиксированной точке $x$ называется предел (2) (при условии, что этот предел существует). Производную функции $y=f(x)$ в данной точке $x$ обозначают одним из символов $f'(x),\, y',\,\dot y ,\, df/dx,\, dy/dx,\, Df(x)$. Операцию нахождения производной (или перехода от функции к её производной) называют дифференцированием.

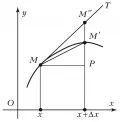
К пределу (2) приводит и задача построения касательной к плоской кривой, определяемой в декартовой системе координат $Oxy$ уравнением $y=f(x)$, в некоторой её точке $M(x, y)$ (рис.). Задав аргументу $x$ приращение $Δx$ и взяв на кривой точку $M'$ с координатами $(x+Δx, f(x+Δx))$, определяют касательную в точке $M$ как предельное положение секущей $MM'$ при стремлении точки $M'$ к $M$ (т. е. при стремлении $Δx$ к нулю). Так как точка $M$, через которую проходит касательная, задана, построение касательной сводится к определению её углового коэффициента (т. е. тангенса угла её наклона к оси $Ox$). Проведя прямую $MP$ параллельно оси $Ox$, получают, что угловой коэффициент секущей $MM'$ равен отношению
$$\frac {PM'}{MP}=\frac{f(x+\Delta x)-f(x)}{\Delta x}.$$В пределе при $Δx\to 0$ угловой коэффициент секущей переходит в угловой коэффициент касательной, который оказывается равным пределу (2), т. е. производной $f'(x)$.

К понятию производной приводит и ряд других задач естествознания. Например, сила тока в проводнике определяется как предел $\lim \limits_{\Delta t\to 0}\Delta q/\Delta t$, где $Δq$ – положительный электрический заряд, переносимый через сечение проводника за время $Δt$, скорость химической реакции определяется как предел $\lim \limits_{\Delta t\to 0}\Delta Q/\Delta t$, где$ΔQ$ – изменение количества вещества за время $Δt$, и вообще, производная некоторой физической величины по времени является скоростью изменения этой величины.

Если функция $y=f(x)$ определена как в самой точке $x$, так и в некоторой её окрестности, и имеет производную в точке $x$, то эта функция непрерывна в точке $x$. Пример функции $y= ∣x∣$ , определённой в любой окрестности точки $x=0$, непрерывной в этой точке, но не имеющей производной при $x= 0$, показывает, что из непрерывности функции в данной точке, вообще говоря, не вытекает существование в этой точке производной. Более того, существуют функции, непрерывные в каждой точке своей области определения, но не имеющие производной ни в одной точке этой области определения.

В случае, когда функция $y=f(x)$ определена только справа или только слева от точки $x$ (например, когда $x$ является граничной точкой отрезка, на котором задана эта функция), вводятся понятия правой и левой производных функции $y=f(x)$ в точке $x$. Правая производная функции $y=f(x)$ в точке $x$ определяется как предел (2) при условии, что $Δx$ стремится к нулю, оставаясь положительным, а левая производная – как предел (2) при условии, что $Δx$ стремится к нулю, оставаясь отрицательным. Функция $y=f(x)$ имеет в точке $x$ производную тогда и только тогда, когда она имеет в этой точке равные друг другу правую и левую производные. Указанная выше функция $y= ∣ x ∣$ имеет в точке $x=0$ правую производную, равную $1$, и левую производную, равную $–1$, и поскольку правая и левая производные неравны друг другу, эта функция не имеет производной в точке $x=0$. В классе функций, имеющих производную, операция дифференцирования является линейной, т. е.$(f(x)+g(x))'=f'(x)+g'(x)$ и $(αf(x))'=αf'(x)$ для любого числа $α$. Кроме того, справедливы следующие правила дифференцирования:

$$[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x);$$

$$\left[\frac{f(x)}{g(x)}\right]'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)},$$если $g(x)≠0$; если $y=f(u)$ и $u=φ(x)$, т. е. $y=f(φ(x))$, то

$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=f'(u)φ'(x).$$Производные некоторых элементарных функций суть:

$$(x^α)'=αx^{α-1}; α \text{ – любое число, }\quad x\gt 0;\\ (\log_ax)'=\frac{1}{x}\log_ae, \quad 0 \lt a≠1,\, \,\,\,\,x \gt 0,$$в частности $(\ln x)'=1/x,\,x \gt 0$;

$$(a^x)'=a^x\ln a,\quad 0 \lt a \neq 1,$$в частности $(ex)'=ex$;

$$\begin{aligned}(\sin x)' &=\cos x, \quad (\cos x)' =–\sin x; \\ (\tan x)'&=\frac{1}{\cos^2 x},\quad x\neq\frac{\pi}{2}+\pi n; \end{aligned}$$

$n=0, ±1, ±2, \ldots$;

$$(\cot x)'=\frac{1}{\sin^2x},\quad x \neq \pi n,$$

$n=0, ±1, ±2, \ldots$;

$$\begin{aligned}(\arcsin x)'&=\frac{1}{\sqrt{(1-x^2)}},\quad -1\lt x\lt1;\\ (\arccos x)'&=\frac{-1}{\sqrt{(1-x^2)}},\quad -1\lt x \lt 1;\\ (\operatorname{arctgx})'&=\frac{1}{(1+x^2)};\\ (\operatorname{arcctgx})'&=\frac{–1}{(1+x^2)}. \end{aligned}$$Производная любой элементарной функции снова является элементарной функцией.

Если производная $f'(x)$, в свою очередь, имеет производную в данной точке $x$, то производную функции $f'(x)$ называют второй производной функции $y=f(x)$ в точке $x$ и обозначают одним из символов $f''(x),\, y'', \,ÿ,\, d^2f/dx^2,\,d^2y/dx^2,\, D^2f(x)$. Для материальной точки, движущейся вдоль оси $Oy$ по закону $y=f(x)$, вторая производная представляет собой ускорение этой точки в момент времени $x$. Аналогично определяются производные любого целого порядка $n$, обозначаемые символами $f^{(n)} (x),\, y^{(n)},\, d^nf/dx^n,\, d^ny/dx^n,\, D^nf(x)$.

Дифференциал

Функция $y=f(x)$, область определения которой содержит некоторую окрестность точки $x$, называется дифференцируемой в точке $x$, если её приращение в этой точке, отвечающее приращению аргумента $Δx$, т. е. величину $Δy=f(x+Δx)-f(x)$ можно представить в виде $Δy=AΔx+αΔx$, где $A=A(x)$, а $α=α(x, Δx)→0$ при $Δx→0$. При этом выражение $AΔx$ называется дифференциалом функции $f(x)$ в точке $x$ и обозначается символом $dy$ или $df(x)$. Геометрически при фиксированном значении $x$ и меняющемся приращении $Δx$

БРЭ. Т. 9БРЭ. Т. 9

дифференциал есть приращение ординаты касательной, т. е. отрезок $PM''$ (рис.). Дифференциал $dy$ является функцией как точки $x$, так и приращения $Δx$. Дифференциал называют главной линейной частью приращения функции, поскольку при фиксированном значении $x$ величина $dy$ является линейной функцией от $Δx$, а разность $Δy-dy$ – бесконечно малой относительно $Δx$ при $Δx→0$. Для функции $f(x)≡x$ по определению $dx=Δx$, т. е. дифференциал независимой переменной $dx$ совпадает с её приращением $Δx$. Это позволяет переписать выражение для дифференциала в виде $dy=Adx$.

Для функции одной переменной понятие дифференциала тесно связано с понятием производной: для того чтобы функция $y=f(x)$ имела в точке $x$ дифференциал, необходимо и достаточно, чтобы она имела в этой точке конечную производную $f'(x)$, при этом справедливо равенство $dy=f'(x)dx$. Наглядный смысл этого утверждения состоит в том, что касательная к кривой $y=f(x)$ в точке с абсциссой $x$ является не только предельным положением секущей, но также и прямой, которая в бесконечно малой окрестности точки $x$ примыкает к кривой $y=f(x)$ теснее, чем любая другая прямая. Т. о., всегда $A(x)=f'(x)$ и запись $dy/dx$ можно понимать не только как обозначение для производной $f'(x)$, но и как отношение дифференциалов функции и аргумента. В силу равенства $dy=f'(x)dx$ правила нахождения дифференциалов непосредственно вытекают из соответствующих правил для производных. Рассматриваются также дифференциалы второго и более высоких порядков.

Приложения

Дифференциальное исчисление устанавливает связи между свойствами функции $f(x)$ и её производных (или её дифференциалов), составляющие содержание основных теорем дифференциального исчисления. Среди этих теорем – утверждение о том, что все точки экстремума дифференцируемой функции $f(x)$, лежащие внутри её области определения, находятся среди корней уравнения $f'(x)=0$, и часто используемая формула конечных приращений (формула Лагранжа) $f(b)-f(a)=f'(ξ)(b-a)$, где $a\lt ξ \lt b$, а также формула Тейлора. Эти утверждения позволяют методами дифференциального исчисления провести исследование поведения функций, обладающих достаточной гладкостью (т. е. имеющих производные достаточно высокого порядка). Они позволяют установить степень гладкости, выпуклость и вогнутость, возрастание и убывание функций, найти их асимптоты, точки перегиба, вычислить кривизну кривой, выяснить характер её особых точек и т. д. Например, условие $f'(x)>0$ влечёт за собой строгое возрастание функции, а условие $f''(x)>0$ – её строгую выпуклость. Кроме того, дифференциальное исчисление позволяет вычислять различного рода пределы функций, в частности пределы отношений двух функций, представляющие собой неопределённости вида $0/0$ или вида $∞/∞$ (см. Раскрытие неопределённостей). Особенно удобно дифференциальное исчисление для исследования элементарных функций, производные которых выписываются в явном виде.

Дифференциальное исчисление функций многих переменных. Методы дифференциального исчисления применяются для исследования функций нескольких переменных. Для функции двух переменных $u=f(x,y)$ её частной производной по $x$ в точке $M(x,y)$ называется производная этой функции по $x$ при фиксированном $y$, определяемая как

$$\lim \limits_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x},$$и обозначаемая одним из символов $f'_x(x,y), u'_x,\partial u/\partial x$ или $\partial f(x,y)/\partial x$. Аналогично определяется и обозначается частная производная функции $u=f(x,y)$ по $y$. Величина $Δu=f(x+Δx, y+Δy) – f(x,y)$ называется полным приращением функции $u$ в точке $M(x,y)$. Если эту величину можно представить в виде $Δu=AΔx+BΔy+\alpha\sqrt {(\Delta x)^2+(\Delta y)^2}$, где $A$ и $B$ не зависят от $Δx$ и $Δy$, а $α$ стремится к нулю при $\sqrt {(\Delta x)^2+(\Delta y)^2}\to 0$, то функция $u=f(x,y)$ называется дифференцируемой в точке $M(x,y)$. Сумму $AΔx+BΔy$ называют полным дифференциалом функции $u=f(x,y)$ в точке $M(x,y)$ и обозначают символом $du$. Так как $A=f'_x(x,y),\, B=f'_y(x,y)$, а приращения $Δx$ и $Δy$ можно взять равными их дифференциалам $dx$ и $dy$, то полный дифференциал $du$ можно записать в виде

$$du=\frac {\partial u}{\partial x}dx+\frac {\partial u}{\partial y}dy.$$Геометрически дифференцируемость функции двух переменных $u=f(x,y)$ в данной точке $M(x,y)$ означает существование у её графика в этой точке касательной плоскости, а дифференциал этой функции представляет собой приращение аппликаты точки касательной плоскости, отвечающей приращениям $dx$ и $dy$ независимых переменных. Для функции двух переменных понятие дифференциала является значительно более важным и естественным, чем понятие частных производных. В отличие от функции одной переменной, для дифференцируемости функции двух переменных $u=f(x, y)$ в данной точке $M(x, y)$ недостаточно существования в этой точке конечных частных производных $f'_x(x, y)$ и $f'_y(x, y)$. Простым достаточным условием дифференцируемости функции $u=f(x, y)$ в точке $M(x, y)$ является существование непрерывных в этой точке частных производных $f'_x(x, y)$ и $f'_y(x, y)$. Аналогично определяются частные производные высших порядков. Частные производные $\partial^2f/\partial x^2$ и $\partial^2f/\partial y^2$, у которых оба дифференцирования ведутся по одной переменной, называют чистыми, а частные производные $\partial^2f/\partial x\partial y$ и $\partial^2f/\partial y\partial x$ – смешанными. В каждой точке, в которой обе смешанные частные производные непрерывны, они равны друг другу. Эти определения и обозначения переносятся на случай большего числа переменных.

Исторический очерк

Отдельные задачи об определении касательных к кривым и о нахождении максимальных и минимальных значений переменных величин были решены математиками Древней Греции. Например, были найдены способы построения касательных к коническим сечениям и некоторым другим кривым. Однако разработанные античными математиками методы были далеки от идей дифференциального исчисления и могли применяться лишь в весьма частных случаях. К середине 17 в. стало ясно, что многие из упомянутых задач вместе с другими (напр., задача определения мгновенной скорости) могут быть решены при помощи одного и того же математического аппарата, при использовании производных и дифференциалов. Около 1666 г. И. Ньютон разработал метод флюксий (см. Исчисление флюксий). Ньютон рассматривал, в частности, две задачи механики: задачу об определении мгновенной скорости движения по известной зависимости пути от времени и задачу об определении пройденного за данное время пути по известной мгновенной скорости. Непрерывные функции времени Ньютон называл флюентами, а скорости их изменения – флюксиями. Таким образом, у Ньютона главными понятиями были производная (флюксия) и неопределённый интеграл (флюента). Он пытался обосновать метод флюксий с помощью теории пределов, которая в то время была развита недостаточно.

В середине 1670-х гг. Г. В. Лейбниц разработал удобные алгоритмы дифференциального исчисления. Основными понятиями у Лейбница являлись дифференциал как бесконечно малое приращение функции и определённый интеграл как сумма бесконечно большого числа дифференциалов. Он ввёл обозначения дифференциала и интеграла, термин «дифференциальное исчисление», получил ряд правил дифференцирования, предложил удобную символику. Дальнейшее развитие дифференциального исчисления в 17 в. шло в основном по пути, намеченному Лейбницем; большую роль на этом этапе сыграли работы Я. Бернулли и И. Бернулли, Б. Тейлора и др.

Следующий этап в развитии дифференциального исчисления связан с работами Л. Эйлера и Ж. Лагранжа (18 в.). Эйлер впервые стал излагать дифференциальное исчисление как аналитическую дисциплину, независимо от геометрии и механики. Он вновь использовал в качестве основного понятия дифференциального исчисления производную. Лагранж пытался строить дифференциальное исчисление алгебраически, пользуясь разложениями функций в степенные ряды; он ввёл термин «производная» и обозначения $y'$ и $f'(x)$. В начале 19 в. была в основном решена задача обоснования дифференциального исчисления на основе теории пределов, главным образом благодаря работам О. Коши, Б. Больцано и К. Гаусса. Глубокий анализ исходных понятий дифференциального исчисления был связан с развитием теории множеств и теории функций действительных переменных в конце 19 – начале 20 вв.