Осо́бая то́чка кри́вой, заданной уравнением $F(x,y)=0$, точка $M_0(x_0,y_0)$, в которой обе частные производные функции $F(x,y)$ обращаются в нуль:

$\left(\dfrac{\partial F}{\partial x}\right)_0=0, \quad\left(\dfrac{\partial F}{\partial y}\right)_0=0.$Если при этом не все вторые частные производные функции $F(x,y)$ в точке $M_0$ равны нулю, то особая точка называется двойной. Если наряду с обращением в нуль первых производных в точке $M_0$ обращаются в нуль и все вторые производные, но не все третьи производные равны нулю и т. д., то особая точка называется тройной, $\ldots, n$-кратной. При исследовании строения кривой вблизи двойной особой точки важную роль играет знак выражения

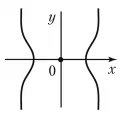
$\displaystyle\Delta=\left(\frac{\partial^2 F}{\partial x^2}\right)_0 \left(\frac{\partial^2 F}{\partial y^2}\right)_0-\left(\frac{\partial^2 F}{\partial x \partial y}\right)_0^2.$Если $\Delta \gt 0$, то особая точка является изолированной; например, у кривой $y^2-x^4+4x^2=0$ начало координат есть изолированная особая точка (рис. 1). Если $\Delta \lt 0$, то особая точка называется узловой или точкой самопересечения; например, у кривой $(x^2+y^2+a^2)^2-4a^2x^2-a^4=0$ начало координат есть узловая особая точка (рис. 2). Если $\Delta=0$, то особая точка является либо изолированной, либо характеризуется тем, что

различные ветви кривой имеют в этой точке общую касательную, например: а) точка возврата (точка заострения) 1-го рода – различные ветви кривой расположены по разные стороны от общей касательной и образуют остриё, как у кривой $y^2-x^3=0$ (рис. 3, а); б) точка возврата (точка заострения) 2-го рода – различные ветви кривой расположены по одну сторону от общей касательной, как у кривой $(y-x^2)^2-x^5=0$ (рис. 3, б); в) точка самоприкосновения (для кривой $y^2-x^4=0$ начало координат является точкой самоприкосновения; рис. 3, в). Наряду с указанными особыми точками, имеется много других особых точек со специальными названиями; например, асимптотическая точка – вершина спирали с бесконечным числом витков (рис. 4), точка прекращения (рис. 5), угловая точка (точка излома) (рис. 6) и т. д.

Рис. 1. Рис. 2. Особая точка кривой.Рис. 1. Рис. 2. Особая точка кривой.