Показа́тельная фу́нкция (экспоненциальная функция, экспонента), функция

$$y=e^z≡\exp z,$$где число $e$ – основание натуральных логарифмов, для любого значения $z$ (действительного или комплексного) определяется соотношением

$$e^z=\lim_{n \rightarrow \infty}\left( 1+\frac{z}{n}\right)^n.\tag{1}$$Её основные свойства

$$e^{z_1}e^{z_2}=e^{z_1+z_2}\quad\text{и}\quad(e^{z_1})^{z_2}=e^{z_1+z_2}$$при любых значениях $z_1$ и $z_2$.

Показательная функция действительного переменного

В курсе математического анализа рассматриваются показательные функции $y=a^x$ при действительных $x$ и $a>0$, $a≠1$; она связана с (основной) показательной функцией $y=e^x$ соотношением

$$a^x=e^{x\ln a}.$$Показательная функция $y=a^x$ определена при всех $x$, положительна, монотонна (возрастает, если $a>1$, и убывает, если $0\lt a\lt 1$), непрерывна, бесконечно дифференцируема; при этом

$$(a^x)'=a^x\ln a,\quad \int a^x dx=\frac{a^x}{\ln a}+C,$$в частности

$$(e^x)'=e^x\ln a,\quad \int e^x dx=e^x+C;$$в окрестности каждой точки показательная функция может быть разложена в степенной ряд, например:

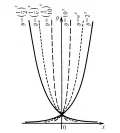
$$e^x=1+\frac{x}{1!}+\ldots+\frac{x^n}{n!}+\ldots\equiv \sum_{n=0}^{\infty}\frac{x^n}{n!},\quad –∞\lt x\lt ∞.\tag{2}$$График показательной функции (экспоненциальная кривая) проходит через точку $(0, 1)$ и асимптотически приближается к оси $Ox$ (рис., где даны графики функций $y=e^x$, $y=\left({1}/{e}\right)^x$, $y=10^x$, $y=\left({1}/{10}\right)^x$, $y=2^x$, $y=\left({1}/{2}\right)^x$); график показательной функции $y=a^x$ симметричен графику показательной функции $y=(1/a)^x$ относительно оси ординат. Если $a>1$, то $a^x$ при $x→∞$ возрастает быстрее любой степени $x$, а при $x→–∞$ стремится к нулю быстрее любой степени $1/x$, т. е. для любого $b>0$,

$$\lim_{x\rightarrow\infty}\frac{a^x}{x^b}=\infty,\quad\lim_{x\rightarrow -\infty}\left|x\right|^ba^x=0.$$Обратной к показательной функции является логарифмическая функция.

Показательная функция часто встречается в приложениях, когда скорость изменения какой-либо величины прямо пропорциональна самой величине, т. е.

$$\frac{dy}{dt}=py.$$Решением этого дифференциального уравнения является показательная функция $y=Ce^{pt}$, где $C$ – постоянная. При $C>0$, $p>0$ эта функция при $t→∞$ экспоненциально возрастает и выражает т. н. закон естественного роста, например рост числа бактерий, увеличение денежного вклада при постоянном процентном приращении. При $C> 0$, $p\lt 0$ показательная функция при $t→∞$ экспоненциально стремится к нулю. С помощью этой функции описываются процесс радиоактивного распада, затухание колебаний и т. п.

Показательная функция комплексного переменного

При комплексных $a$ и $z=x+iy$ показательная функция $a^z$ связана с (основной) показательной функцией $e^z$ соотношением

$$a^z=e^{z\,\text{Ln}\,a},$$где $\text{Ln}\, a$ – логарифм комплексного числа $a$. Показательная функция $e^z$ – целая трансцендентная функция и является аналитическим продолжением показательной функции $e^x$ с действительной оси в комплексную плоскость.

Помимо формулы (1), показательная функция может быть определена также с помощью ряда (2), сходящегося во всей комплексной плоскости, или по формуле Эйлера

$$e^z=e^{x+iy}=e^x(\cos y+i\sin y).$$Справедливы равенства

$$|e^z|=e^х,\quad \text{Arg} \, e^z=y+2kπ, \, k= 0,± 1,± 2,\ldots$$Показательная функция $e^z$ – периодическая с периодом $2πi$, т. е. $e^{z+2πi}=e^z$. Показательная функция $e^z$ принимает все комплексные значения, за исключением нуля; уравнение $e^z=a$ имеет бесконечное множество решений для любого комплексного числа $a≠0$, эти решения находятся по формуле

$$z=\text{Ln}\,a=\ln |a|+i\text{Arg}\, a.$$Показательная функция $e^z$ – одна из основных элементарных функций. Через неё выражаются, например, тригонометрические функции и гиперболические функции. Показательная функция комплексного переменного играет важную роль в приложениях, например в теории рядов и интегралов Фурье, в теории колебаний и распространения волн.