Тригонометри́ческие фу́нкции, элементарные функции синус, косинус, тангенс, котангенс, секанс, косеканс. Обозначаются соответственно $\sin \alpha$, $\cos \alpha$, $\tg \alpha$, $\ctg \alpha$, $\sec \alpha$, $\cosec \alpha$. Используются и другие обозначения, например $\tan \alpha$ (для тангенса), $\cot \alpha$, $\cotg \alpha$ и $\mathop{\mathrm{ctn}} \alpha$ (для котангенса), $\csc \alpha$ (для косеканса).

Для наглядного изображения аргументов и значений тригонометрических функций используется тригонометрическая окружность – окружность единичного радиуса с центром в начале координат (рис. 1).

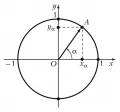Рис. 1. Тригонометрическая окружность. БРЭ. Т. 32.Рис. 1. Тригонометрическая окружность. БРЭ. Т. 32.Пусть $A$ – точка на тригонометрической окружности, $α$ – угол между осью абсцисс и вектором $OA$, отсчитываемый от положительного направления оси абсцисс. Если отсчёт ведётся против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке – отрицательной.

Тригонометрические функции синус и косинус по определению равны декартовым прямоугольным координатам $(x_α, y_α)$ точки $A$:$$\sin\alpha=y_\alpha,\qquad \cos{\alpha}=x_\alpha.$$Остальные тригонометрические функции определяются следующими равенствами: $$\tg\alpha=\frac{\sin{\alpha}}{\cos{\alpha}},\qquad\ctg\mathrm\alpha=\frac{\cos{\alpha}}{\sin{\alpha}},\qquad\sec{\alpha}=\frac{1}{\cos{\alpha}},\qquad\cosec\alpha=\frac{1}{\sin{\alpha}}.$$Функции секанс и косеканс используются редко, обычно их выражают через синус и косинус.

В тригонометрии угол как вещественный аргумент тригонометрических функций принято измерять в угловых градусах или в радианах. Аргумент изменяется от $-\infty$ до $+\infty$. Чаще используется радианное измерение, при этом обозначение «радиан» опускается и тригонометрические функции считаются функциями числового аргумента. При радианном измерении считается, что $α$ есть взятая с соответствующим знаком длина дуги единичной окружности, соединяющей точки $(1, 0)$ и $A$, при этом допускается, что эта дуга, прежде чем закончиться в точке $A$, делает несколько полных оборотов. Точку $A$ называют ещё точкой $α$, при этом нужно иметь в виду, что числам $α$ и $α + 2kπ$, $k = 0, \pm 1, \pm 2, \ldots$ соответствует одна и та же точка единичной окружности. Точки окружности делятся на четверти (квадранты), в каждой четверти тригонометрические функции имеют определённый знак (рис. 2).

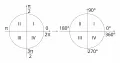Рис. 2. Четверти (квадранты) тригонометрической окружности. Архив БРЭ.Рис. 2. Четверти (квадранты) тригонометрической окружности. Архив БРЭ.Знаки тригонометрических функций приведены в таблице 1.

Таблица 1

В таблице 2 приведены значения тригонометрических функций некоторых углов.

Таблица 2

Для углов, величины которых лежат между $0$ и $\dfrac{\pi}{2}$, значения тригонометрических функций можно определять как отношения сторон прямоугольного треугольника. На рис. 3 показан прямоугольный треугольник с катетами $a$ и $b$ и гипотенузой $c$.

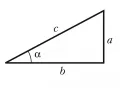Рис. 3. БРЭ. Т. 32.Рис. 3. БРЭ. Т. 32.Для угла $\alpha$, противолежащего катету $a$, справедливы следующие равенства:

$$\sin\alpha=\frac ac, \quad \cos\alpha=\frac bc, \quad \tg\alpha=\frac ab, \quad \ctg\alpha=\frac ba,\quad \sec\alpha=\frac cb, \quad \cosec\alpha=\frac ca.$$На рис. 4 показано представление тригонометрических функций как отрезков, связанных с единичной окружностью: $$\begin{gathered}\sin\alpha=AB,\quad \cos\alpha=OB,\quad \tg\alpha=CD,\quad \ctg\alpha=EF,\\ \sec\alpha=OC,\quad \cosec\alpha=OF.\end{gathered}$$

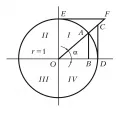Рис. 4. БРЭ. Т. 32.Рис. 4. БРЭ. Т. 32.С этими отрезками связано происхождение названий тригонометрических функций. Так, латинское слово tangens означает «касающийся» ($CD$ – отрезок касательной к окружности), латинское secans означает «секущая» ($OC$ – отрезок секущей к окружности). Название «синус» (лат. sinus – пазуха) – перевод арабского слова «джайб», являющегося, по-видимому, искажением санскритского слова «джива» (буквально – тетива лука), которым индийские математики обозначали синус. Названия «косинус», «котангенс» и «косеканс» происходят от сокращённого слова complementi (дополнение). Например, «косинус» – от complementi sinus («синус дополнения»). Это связано с тем, что $\cos{\alpha}$, $\ctg \alpha$ и $\cosec\alpha$ равны соответственно синусу, тангенсу и секансу аргумента, дополняющего $\alpha$ до $\dfrac{\pi}{2}$: $$\cos\alpha=\sin\left(\frac\pi2-\alpha\right),\qquad \ctg\alpha=\tg\left(\frac\pi2-\alpha\right), \qquad \cosec\alpha=\sec\left(\frac\pi2-\alpha\right).$$Тригонометрические функции $\sin{\alpha}$ и $\cos{\alpha}$ определены при всех действительных $\alpha$, множество значений этих функций – отрезок$[–1, 1]$. Функция $\tg\alpha$ определена при всех действительных $\alpha$, таких, что $\alpha\neq\dfrac{\pi}{2}+k\pi,\ k=0,\ \pm1,\ \pm2,\ldots$ Функция $\ctg\alpha$ определена при всех действительных $\alpha$, таких, что $\alpha\neq k\pi,\ k=0,\ \pm1,\ \pm2,\ldots$ Множеством значений функций $\tg \alpha$ и $\ctg \alpha$ является множество всех действительных чисел.

Все тригонометрические функции являются периодическими функциями. Наименьший положительный период функций синус и косинус равен $2\pi$, т. е. для любого действительного $\alpha$ $$\sin\left(\alpha+2\pi\right)=\sin\alpha,\qquad \cos\left(\alpha+2\pi\right)=\cos\alpha.$$Наименьший положительный период функций тангенс и котангенс равен $\pi$, т. е. для любого действительного $\alpha$ из области определения этих функций $$\tg\left(\alpha+\pi\right)=\tg \alpha,\qquad \ctg\left(\alpha+\pi\right)=\ctg \alpha.$$Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Производные и интегралы от тригонометрических функций задаются следующими формулами:

$$(\sin\alpha)'=\cos\alpha, \qquad (\cos\alpha)'=-\sin\alpha,\\ (\tg\alpha)'=\frac{1}{\cos^2\alpha}, \qquad (\ctg\alpha)'=\frac{1}{\sin^2\alpha},\\ \begin{aligned} \int\sin\alpha\,d\alpha&=-\cos\alpha+C,\\ \int\cos\alpha\,d\alpha&=\sin\alpha+C,\\ \int\tg\alpha\, d\alpha&=-\ln\ |\cos\alpha|+C,\\ \int\ctg\alpha\, d\alpha&=\ln\ |\sin\alpha|+C, \end{aligned}$$где $C$ – постоянная.

Все тригонометрические функции допускают разложение в степенные ряды. Ряды для синуса и косинуса имеют вид

$$\begin{aligned}\sin{\alpha}&=\alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-\ldots+{(-1)}^n\frac{\alpha^{2n+1}}{(2n+1)!}+\ldots,\\ \cos{\alpha}&=1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-\ldots+{(-1)}^n\frac{\alpha^{2n}}{(2n)!}+\ldots\end{aligned}$$Эти ряды сходятся при всех действительных $α$, отрезки этих рядов можно использовать для получения приближённых значений синуса и косинуса при малых значениях аргумента:$$\begin{aligned} \sin{\alpha}&\approx\alpha-\frac{\alpha^3}{6}\approx\alpha,\\ \cos{\alpha}&\approx1-\frac{\alpha^2}{2}+\frac{\alpha^4}{24}\approx1-\frac{\alpha^2}{2}. \end{aligned}$$Ряды для тангенса и котангенса имеют вид

$$\begin{aligned} \tg\alpha&=\alpha+\frac{\alpha^3}{3}+\frac{{2\alpha}^5}{15}+\frac{{17\alpha}^7}{315}+...,\qquad |\alpha|<\frac{\pi}{2},\\ \ctg\alpha&=\frac{1}{\alpha}-\frac{\alpha}{3}-\ \frac{\alpha^3}{45}-\frac{{2\alpha}^5}{945}-...,\qquad 0<|\alpha|<\pi.\ \ \ \end{aligned}$$Функции, обратные тригонометрическим функциям (обратные тригонометрические функции), являются многозначными; для их обозначения используется префикс $\mathrm{Arc}$ (например, $\mathrm{Arcsin}$, $\mathrm{Arccos}$). Для обозначения главных ветвей этих функций используется префикс $\mathrm{arc}$ (например, $\arcsin$, $\arccos$).

Тригонометрические функции определяются также для комплексных значений аргумента как аналитические продолжения тригонометрических функций действительного аргумента, либо с помощью формул Эйлера их можно определить через экспоненту.

Тригонометрические функции появились в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся, по существу, тригонометрическими функциями, встречаются уже в работах математиков Древней Греции – Евклида, Архимеда, Аполлония Пергского и др. Однако эти соотношения не являлись у них самостоятельным объектом исследования, так что тригонометрические функции как таковые ими не изучались. Тригонометрические функции рассматривались как отрезки и в таком виде применялись Аристархом Самосским, Гиппархом, Менелаем и Птолемеем при решении сферических треугольников. Птолемей составил первую таблицу хорд для острых углов через $30^\prime$ с точностью до $10^{–6}$; это была первая таблица синусов. Формулы преобразования сумм тригонометрических функций в произведения выводились Региомонтаном и Дж. Непером в связи с изобретением последним логарифмов (1614). Региомонтан составил таблицу синусов через $1^\prime$. Разложения тригонометрических функций в степенные ряды были получены И. Ньютоном в 1669 г. В современную форму теорию тригонометрических функций привёл Л. Эйлер, который предложил и принятую ныне символику.