Интегра́льное представле́ние аналити́ческой фу́нкции, представление аналитической функции в виде интеграла, зависящего от параметра. Интегральные представления аналитических функций возникли на ранних стадиях развития теории функций и математического анализа вообще как удобный аппарат для обозримого представления аналитических решений дифференциальных уравнений, для исследования асимптотики этих решений и их аналитического продолжения. Несколько позже интегральные представления аналитических функций нашли применения для решения граничных задач теории аналитических функций и сингулярных интегральных уравнений, исследования внутренних и граничных свойств аналитических функций различных классов, а также для решения других, самых разнообразных вопросов математического анализа. В процессе развития теории функций изучение свойств отдельных, наиболее важных, типов интегральных представлений аналитических функций обособлялось в виде самостоятельных глав теории функций (см., например, Интеграл Коши, Интеграл Пуассона, Интеграл Шварца).

Обширный класс интегральных представлений аналитических функций, используемых для получения и исследования аналитических решений дифференциальных уравнений, описывается общей формулой:
$$\tag{1} f(z)=\int_L K(z, \zeta) v(\zeta)\, d \zeta,$$где $K(z, \zeta)$ – ядро интегрального представления, $v(\zeta)$ – плотность и $L$ – контур (или система контуров) в совмещённой плоскости комплексных переменных $z$, $\zeta$. Целесообразное и по возможности наиболее простое решение трёх взаимосвязанных вопросов о выборе ядра $K$, плотности $v$ и контура $L$ для представления данной функции $f(z)$ (или данного класса функций) является определяющим с точки зрения успешного применения метода интегрального представления аналитической функции. При этом свойства представления $(1)$ в первую очередь существенно зависят от того, является ли ядро $K(z, \zeta)$ целой функцией комплексных переменных $z, \zeta$, или же ядро $K(z, \zeta)$ сингулярное, т. е. имеет те или иные особенности. Вообще говоря, ядро интегрального представления аналитической функции не обязательно является аналитической функцией переменных $z, \zeta$ – аналитичность функции $f(z)$ может обеспечиваться за счёт специфических свойств плотности. Формула $(1)$ как формула простого однократного интегрирования также, вообще говоря, не обязательна – имеются типы интегрального представления аналитической функции, в которых используются повторные интегралы.

Общая схема получения интегральных представлений специальных функций $f(z)$, являющихся решениями некоторого обыкновенного дифференциального уравнения $\mathfrak{L}_z[f](z)=0$, сводится в основном к следующему. За счёт целесообразного выбора, чаще всего несингулярного, ядра $K$ должна оказаться осуществимой следующая переброска действия оператора $\mathfrak{L}_z$:
$$\tag{2} \begin{aligned} \mathfrak{L}_z[f](z)&=\int_L \mathfrak{L}_z[K](z, \zeta) v(\zeta) \,d \zeta= \\ & =\int_L \mathfrak{M}_\zeta[K](z, \zeta) v(\zeta) \,d \zeta= \\ & =\int_L K(z, \zeta) \tilde{\mathfrak{L}}_\zeta[v](\zeta)\, d \zeta+P[v, K], \\ \end{aligned}$$т. е. ядро должно в первую очередь удовлетворять по возможности простому уравнению с частными производными $\mathfrak{L}_z[K]=\mathfrak{M}_{\zeta}[K]$, допускающему последующее интегрирование по частям с целью восстановления первоначального вида ядра под интегралом и переброску действия получающегося при этом сопряжённого оператора $\tilde{R}_\zeta$ на плотность $v$. Получив формулу вида $(2)$, подбирают достаточно простую плотность $v$, удовлетворяющую сопряжённому уравнению $\tilde{\mathfrak{L}}_\zeta[v](\zeta)=0$, и контур $L$, обеспечивающий обращение в нуль обинтегрированного члена $P[v, K]$. При этом необходимо иметь в виду, что выбор контура $L$ определяет частное решение исходного уравнения $\mathfrak{L}_z[f](z)=0$. Наибольшее применение находят ядра:

$$\begin{aligned} & K(z, \zeta)=e^{z \zeta} \text { или } K(z, \zeta)=e^{i z \zeta}, \\ & K(z, \zeta)=z^\zeta \text { и } K(z, \zeta)=(z-\zeta)^\alpha, \end{aligned}$$иногда называемые соответственно ядром Лапласа – Фурье, ядром Меллина и ядром Эйлера. Различные замены переменных приводят к видоизменённым формам ядер. В описанном виде получение интегрального представления аналитической функции самым тесным образом связано с методом интегральных преобразований.

Таким путём, например, получается известное интегральное представление функций Бесселя:
$$\tag{3} J_p(z)=\frac{\Gamma(1 / 2-p)}{2 i \pi^{3 / 2}}\left(\frac{z}{2}\right)^p \int_L e^{i z \zeta}\left(\zeta^2-1\right)^{p-1 / 2}\, d \zeta,$$где контур $L$ имеет вид восьмёрки, охватывающей точки $-1$ и $+1$. Представление $(3)$ характерно, с одной стороны, тем, что его плотность $v(\zeta)=\left(\zeta^2-1\right)^{p-1 / 2}$ гораздо проще, чем представляемые трансцендентные функции $J_p(z)$, a c другой стороны – тем, что оно позволяет довольно просто обозреть свойства функций $J_p(z)$ и, в частности, изучить их асимптотику.

Целесообразное изменение контура $L$ позволяет осуществить аналитическое продолжение, т. е., иными словами, позволяет получить интегральное представление аналитической функции, пригодное во всей её области существования. Например, интеграл Эйлера второго рода:

$$\Gamma(z)=\int_0^{\infty} t^{z-1} e^{-t} \,d t, \quad \operatorname{Re} z>0,$$представляет гамма-функцию $\Gamma(z)$ при $\mathrm{Re}\,z>0$, а если выбрать контур интегрирования $L_1$ в виде петли (рис. 1), то получается интегральное представление

$$\Gamma(z)=\frac{1}{e^{2 i \pi z}-1} \int_{L_1} \zeta^{z-1} e^{-\zeta} \,d \zeta,$$пригодное для всех $z$, кроме точек $z=-1,-2, \ldots$, в которых $\Gamma(z)$ имеет простые полюсы.

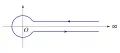Рис. 1.Рис. 1.Аналогично, аналитическое продолжение интеграла Эйлера первого рода:

$$\mathrm{B}(z, w)=\int_0^1 t^{z-1}(1-t)^{w-1} \,d t, \quad \operatorname{Re} z>0, \quad \operatorname{Re} w>0,$$выражающего бета-функцию $\mathrm{B}(z, w)$ при $\mathrm{Re}\, z>0$, $\operatorname{R e} w>0$, осуществляется путём перехода к контуру интегрирования в виде двойной петли $L_2$ (рис. 2).

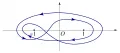Рис. 2.Рис. 2.Изучались интегральные представления специальных функций (см. Смирнов. 1974; Кратцер. 1963); интегральные представления весьма обширных классов функций в связи с интегральными преобразованиями (Джрбашян. 1966).

Универсальный характер в теории аналитических функций имеют сингулярное ядро Коши

$$K(z, \zeta)=\frac{1}{2 \pi i} \frac{1}{(\zeta-z)}$$и соответствующее интегральное представление аналитической функции – интеграл Коши:
$$\tag{4} f(z)=\frac{1}{2 \pi i} \int_L \frac{f(\zeta) \, d \zeta}{\zeta-z} \text {. }$$Это интегральное представление аналитической функции выражает значения однозначной аналитической функции $f(z)$ в области $D$, ограниченной простым замкнутым контуром $L$ (или системой таких контуров), например, в случае, когда функция $f(z)$ непрерывна в замкнутой области $\bar{D}=D \cup L$; в дополнительной области $C \bar{D}$, $\infty \in C \bar{D}$, интеграл из правой части $(4)$ тождественно обращается в нуль. Фундаментальная роль представления $(4)$ в теории аналитических функций обусловливается тем, что интеграл Коши есть свёртка $f(z)$ с фундаментальным решением $1/2\pi iz$ оператора Коши – Римана

$$\frac{\partial}{\partial \bar{z}}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i \frac{\partial}{\partial y}\right),$$поэтому из представления $(4)$ получаются все основные свойства аналитических функций. С точки зрения общих свойств интегрального представления аналитической функции интеграл Коши выделяется особенно простой структурой ядра и тем, что плотность $v(\zeta)=f(\zeta)$ совпадает со значениями представляемой функции на контуре $L$. Это последнее свойство остаётся в силе, если под интегралом $(4)$ заменить ядро Коши $1/2\pi i(\zeta-z)$ на любую однозначную аналитическую по $z$ в замкнутой области $\bar{D}$ функцию $K(z, \zeta)$, имеющую в точке $z=\zeta$ простой полюс с вычетом $1$. Среди таких функций $K(z, \zeta)$ ядро Коши наиболее простое, но указанная свобода выбора ядра в интеграле Коши часто используется при решении граничных задач.

Совпадение плотности $v(\zeta)$ с граничными значениями $f(\zeta)$ аналитической функции $f(z)$ в сущности есть лишь форма выражения свойства аналитичности. При использовании интегрального представления $(4)$ с априори произвольно заданной плотностью $v(\zeta)$ получается интеграл типа Коши, в котором связь плотности с граничными значениями выражается гораздо сложнее через сингулярный интеграл по контуру $L$.

В граничных задачах теории аналитических функций для решения сингулярных интегральных уравнений роль интегралов типа Коши и их модификаций исключительно важна (см. Мусхелишвили. 1968; Гахов. 1977).

При исследовании внутренних и граничных свойств аналитических функций различных классов применяются более общие интегральные представления аналитических функций, чем $(1)$, в виде зависящих от параметра интегралов
$$\tag{5} f(z)=\int_L K(z, \zeta) d \mu(\zeta)$$по борелевской граничной мере $\mu$, вообще говоря комплексной, сосредоточенной на ограничивающем область $D$ контуре $L$ и выражающейся при помощи той или иной процедуры через представляемую функцию $f(z)$.

Например, все функции $f(z)$, регулярные в единичном круге $D=\{z ;|z|<1\}$ и имеющие положительную действительную часть, $\operatorname{Re} f(z)>0$, характеризуются представимостью по формуле Герглотца:

$$f(z)=\int \frac{\zeta+z}{\zeta-z} d \mu(\zeta)+i c, \quad \operatorname{Im} c=0,$$идея которой по существу восходит к интегралу Шварца. Здесь $\mu$ – произвольная положительная мера, сосредоточенная на окружности $L=\{\zeta ;|\zeta|=1\}$. В теории однолистных функций находят существенные применения и другие весьма разнообразные интегральные представления аналитической функции вида $(5)$, известные также под названиями параметрических представлений, или структурных формул. Так, для класса типично вещественных функций $f(z)=z+c_2 z^2+\ldots$ в круге $D=\{z ;|z|<1\}$ [т. е. таких, что $\operatorname{Im} f(x)=0$ при $-1<x<1$ и $\operatorname{Im}f(z) \times \operatorname{Im} z>0$ при $\operatorname{Im} z \neq 0$] характерно представление

$$f(z)=\int \frac{z\, d \mu(\zeta)}{(z-\zeta)(z-\bar{\zeta})},$$где $\mu$ – произвольная положительная мера, сосредоточенная на окружности $L=\{\zeta ;|\zeta|=1\}$ и нормированная условием $\displaystyle\|\mu\|=\int d \mu(\xi)=1$. Часто применяются также модификации представления $(5)$ в виде

$$f(z)=\varphi\left\{\int K(z, \zeta)\, d \mu(\zeta)\right\},$$где $\varphi: \mathbb{C} \rightarrow \mathbb{C}$ – некоторая особо подбираемая, по возможности простая функция, например $\varphi(z)=\exp z$.

Исходя из понимания меры $\mu$ как функционала, интегральное представление аналитической функции $(5)$ можно истолковать как значение $\langle\mu \zeta, K(z, \zeta)\rangle$ функционала $\mu$ на ядре $K(z, \zeta)$. Следовательно, развитием метода интегрального представления аналитической функции является аналитическое представление обобщённых функций $V$ в виде значения $V$ на ядре $K(z, \zeta)$:
$$\tag{6} \hat{V}(z)=\langle V_{\zeta}, K(z, \zeta)\rangle.$$При этом в дополнении носителя обобщённой функции $V$ функция $\hat{V}(z)$ является аналитической [ядро $K(z, \zeta)$ предполагается аналитическим по $z$ при $z \neq \zeta$]. Представления вида $(6)$ находят важные применения в математической физике (см. Бремерман. 1968; Владимиров. 1979).

В теории аналитических функций $f(z)$ нескольких комплексных переменных $z=\left(z_1, \ldots, z_n\right)$, $n \geqslant 1$, интегральные представления аналитических функций простейшего вида выражаются общей формулой:
$$\tag{7} f(z)=\int v(\zeta) \omega(z, \zeta),$$где $v(\zeta)$ – плотность, так или иначе связанная с $f(z)$, $\omega(z, \zeta)$ – дифференциальная форма по переменным $\zeta=\left(\zeta_1, \ldots, \zeta_n\right)$, $\bar{\zeta}=\left(\bar{\zeta}_1, \ldots, \bar{\zeta}_n\right)$, коэффициенты которой зависят от параметров $z=\left(z_1, \ldots, z_n\right)$, $\bar{z}=\left(\bar{z}_1, \ldots, \bar{z}_n\right)$, причём интегрирование производится по всей границе $\partial D$ области определения $D$ функции $f(z)$ или по некоторой её части. Употребляются и представления в виде линейной комбинации интегралов типа $(7)$. Например, функция $f(z)$, голоморфная в полукруговой области $D= D_1 \times \ldots \times D_n$ и непрерывная в замыкании $D$, всюду в $D$ представима в виде интеграла Коши:

$$f(z)=\int f(\zeta) \omega(z, \zeta),$$где дифференциальная форма $\omega$ имеет особенно простой вид

$$\omega(z, \zeta)=\frac{1}{(2 \pi i)^n} \frac{d \zeta_1 \wedge \ldots \wedge d \zeta_n}{\left(\zeta_1-z_1\right) \ldots\left(\zeta_n-z_n\right)}=K(z, \zeta)\, d \zeta,$$а интегрирование производится по остову $\Gamma=\partial D_1 \times \ldots\times \partial D_n$ области $D$ (см. Представление Бергмана – Вейля, Формула Лере, Представление Бохнера – Мартинелли, a также Владимиров. 1964; Шабат. 1976).

Как и в случае одного комплексного переменного, дальнейшим развитием интегральных представлений аналитических функций $(7)$ являются представления вида:

$$f(z)=\langle V \zeta, K(z, \zeta)\rangle$$или

$$f(z)=\left\langle V_\zeta, \omega(z, \zeta)\right\rangle,$$выражающие аналитическую функцию $f(z)$ в некоторой области в виде значения функционала $V$ на ядре $K(z, \zeta)$ или на форме-ядре $\omega(z, \zeta)$. При этом $V$ интерпретируется, соответственно, как обобщённая функция на определённом пространстве функций или как поток на определённом пространстве дифференциальных форм.