Непреры́вная фу́нкция, функция, значения которой мало изменяются при малых изменениях аргумента. Точнее, функция $f(x)$, определённая на интервале $(a, b)$, называется непрерывной в точке $x_0∈ (a, b)$, если для любого $ε>0$ существует $δ>0$ такое, что $|f(x)-f(x_0)|<ε$ для всех $x$ таких, что $|x-x_0|<δ$. В этом определении число $δ$, зависящее от $ε$, может зависеть и от $x_0$. Это определение равносильно следующему: для любой последовательности $x_1, x_2,\dots$ такой, что $x_n→x_0$ при $n→∞$, последовательность $f(x_1), f(x_2),\dots$ такова, что $f(x_n)→f(x_0)$ при $n→∞$. Иначе говоря, $\lim\limits_{n\rightarrow\infty}f(x_n)=f(\lim\limits_{n\rightarrow \infty}x_n)$ для всех последовательностей, сходящихся к $x_0$.

Если условие, указанное в определении непрерывной функции, выполняется лишь при $x⩾x_0$ или лишь при $x⩽x_0$, то функция $f(x)$ называется соответственно непрерывной справа или слева в точке $x_0$. Функция $f(x)$ называется непрерывной на интервале$(a, b)$, если она непрерывна в каждой точке $x∈ (a, b)$. Функция $f(x)$ называется непрерывной на отрезке $[a, b]$, если она непрерывна на интервале $(a, b)$ и в точке $a$ она непрерывна справа, а в точке $b$ – слева.

Одна и та же функция может быть непрерывной для одних значений аргумента и иметь точки разрыва при других значениях. Так, дробная часть числа $x$ (её принято обозначать 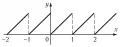$\{x\}$, Рис.1. График дробной части числа x.Рис.1. График дробной части числа x.например, $\{1,25\}=0,25,\: \{\pi\}=0,14159\dots,\: \{2\}=0$) является разрывной функцией при целых значениях аргумента и непрерывной при всех других значениях (рис. 1), причём в точках разрыва она непрерывна справа.

Простейшие элементарные функции $x^n,$ $n=1, 2, \dots,$ $a^x,\: a>0,$ $\sin{x}, \:\cos{x}$ непрерывны при всех действительных $x$. Сумма, разность и произведение непрерывных функций вновь являются непрерывными функциями. Частное двух непрерывных функций является непрерывной функцией для тех значений аргумента, где знаменатель не обращается в нуль. Если функция $g(x)$ непрерывна в точке $x_0$, а функция $f(y)$ непрерывна в точке $y_0=g(x_0)$, то сложная функция $f(g(x))$ непрерывна в точке $x_0$. Если функция $f(x)$ непрерывна и строго возрастает на $[a, b]$, то обратная функция $f^{–1}(y)$ существует, строго возрастает и непрерывна на $[f(a), f(b)]$; аналогичное утверждение справедливо для строго убывающих функций.

Непрерывные функции обладают многими важными свойствами, которыми объясняется значение этих функций в математике и её приложениях. Функция, непрерывная на отрезке, ограничена на нём и достигает на нём наибольшего и наименьшего значений, кроме того, она принимает на этом отрезке все промежуточные значения, лежащие между её наименьшим и наибольшим значениями. Для любой функции, непрерывной на отрезке$[a, b]$, существует многочлен, значения которого отличаются на этом отрезке от значений функции менее, чем на произвольное сколь угодно малое, наперёд заданное число (теорема Вейерштрасса о приближении непрерывных функций многочленами). Функции, непрерывные на отрезке, обладают свойством равномерной непрерывности.

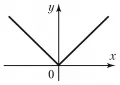Рис. 2. График функции y =|x|.Рис. 2. График функции y =|x|.Любая функция, непрерывная на некотором отрезке, интегрируема на нём. Однако не всякая непрерывная функция имеет производную. Геометрически это означает, что график непрерывной функции не обязательно обладает касательной в каждой точке; это может быть связано с тем, что график имеет угловую точку (рис. 2, функция $y= |x|$), или с тем, что он совершает в окрестности какой-либо точки бесконечно много колебаний между двумя пересекающимися прямыми (рис. 3, функция $y=x\sin{|1/x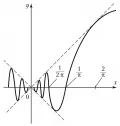|}$ при $x≠0$ и $y=0$ при $x=0$). Рис. 3. График функции, совершающей в окрестности точки (0, 0) бесконечно много колебаний между двумя пересекающимися прямыми.Рис. 3. График функции, совершающей в окрестности точки (0, 0) бесконечно много колебаний между двумя пересекающимися прямыми.Существуют непрерывные функции, не имеющие производной ни в одной точке, первый пример такого рода был предложен Б. Больцано в 1830 г.

Функция $f(x, y, z,\dots)$ нескольких переменных, определённая в некоторой окрестности точки $(x_0, y_0, z_0,\dots)$, называется непрерывной (по совокупности переменных $x, y, z, \dots$) в этой точке, если для любого $ε>0$ можно указать такое $δ> 0$, что при одновременном выполнении неравенств$$|x-x_0|<δ,\: |y-y_0|<δ, \:|z-z_0|<δ, \:\dots$$выполняется также и неравенство$$|f(x, y, z, \dots)-f(x_0, y_0, z_0, \dots)|<ε.$$Такая функция является непрерывной по каждому аргументу в отдельности (если остальным переменным приданы определённые числовые значения). Обратное, вообще говоря, не верно: функция $f(x, y, z, ...)$, непрерывная по каждому аргументу в отдельности, может и не быть непрерывной функцией по совокупности аргументов. Такой пример даёт функция $f(x, y)$, равная $\frac{xy}{x^2+y^2}$, если $x^2+y^2≠0$, и равная $0$ при $x=y=0$. Она непрерывна по $x$ при любом фиксированном $y$ и непрерывна по $y$ при любом фиксированном $x$. В частности, она непрерывна по $x$ при $y=0$ и по $y$ при $x=0$. Если же положить $y=x$, то значение функции будет при всех $x≠0$ равным ${x^2}/({x^2+y^2})={1}/{2}$, и для $0<ε<1/2$ нельзя указать такое число $δ>0$, чтобы при одновременном выполнении неравенств $|x|<δ$, $|y|<δ$ выполнялось неравенство $\left|\frac{xy}{x^2+y^2}\right|<ε$. На непрерывные функции нескольких переменных распространяются все основные теоремы, относящиеся к непрерывным функциям одного переменного.