Симме́три́я (лат. symmetria, греч. συμμετρία – соразмерность) в математике, 1) симметрия (в узком смысле), или (зеркальное) отражение относительно плоскости $α$ в пространстве (относительно прямой $α$ на плоскости), – преобразование пространства (плоскости), при котором каждая точка $M$ переходит в точку $M´$ такую, что отрезок $MM´$ перпендикулярен плоскости (прямой) $α$ и делится ею пополам. Плоскость (прямая) $α$ называется плоскостью (осью) симметрии (рис. 1).

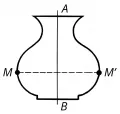Рис. 1. Ось симметрии.Рис. 1. Ось симметрии.2) Симметрия (в широком смысле) – свойство геометрической фигуры $Φ$ совмещаться с собой при действии некоторой группы $G$ (см. Теория групп) ортогональных преобразований, называемой группой симметрии $Φ$. При этом преобразование $A$ евклидова пространства называется ортогональным, если оно сохраняет скалярное произведение любых векторов $x, y$, т. е. $(Ax,Ay)=(x,y)$. Ортогональные преобразования и только они сохраняют длины векторов и углы между ними. Таким образом, симметрия отражает некоторую правильность формы фигуры, её инвариантность при действии преобразований из $G$. Например, если фигура $Φ$ на плоскости такова, что повороты относительно некоторой точки $O$ на угол $360°/n$, $n⩾2$ – целое, переводят её в себя, то говорят, что $Φ$ обладает симметрией $n$-го порядка, а $O$ называют центром симметрии $n$-го порядка (рис. 2).

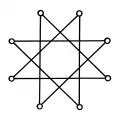Рис.2. Симметрия 8-го порядка.Рис.2. Симметрия 8-го порядка. Окружность обладает симметрией бесконечного порядка, поскольку совмещается с собой при повороте вокруг центра на любой угол.

Простейшими видами пространственной симметрии, помимо симметрии, порождённой отражениями, являются следующие:

а) симметрия порядка $n$ относительно прямой; в этом случае фигура совмещается с собой вращением вокруг некоторой прямой (оси симметрии) на угол $360°/n$. Например, плоская фигура в пространстве, симметричная относительно некоторой прямой, имеет в пространстве эту прямую осью симметрии 2-го порядка.

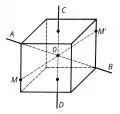Рис. 3. Симметрия куба.Рис. 3. Симметрия куба.Для куба (рис. 3) прямая $AB$ является осью симметрии 3-го порядка, а прямая $CD$ – осью симметрии 4-го порядка; вообще правильные и полуправильные многогранники симметричны относительно ряда прямых;

Рис. 4. Перенос и отражение.Рис. 4. Перенос и отражение.

б) симметрия переноса; в этом случае фигура совмещается с собой переносом вдоль некоторой прямой (оси переноса) на некоторый отрезок. Фигура с одной осью переноса обладает бесконечным множеством плоскостей симметрии, перпендикулярных оси переноса, поскольку любой перенос можно осуществить двумя последовательными отражениями (рис. 4). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.

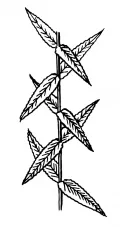Рис. 5. Винтовая симметрия.Рис. 5. Винтовая симметрия.

Комбинации симметрий, порождённые отражениями и вращениями (исчерпывающие простейшие виды симметрий конечных фигур), а также переносами, представляют интерес и являются предметом исследования в различных областях естествознания, искусства и т. д.

Например, винтовая симметрия, порождённая поворотом на некоторый угол вокруг оси и переносом вдоль той же оси, наблюдается в расположении листьев у растений (рис. 5).