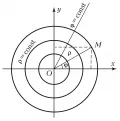
Поля́рная систе́ма координа́т, система координат на плоскости, в которой координатами точки служат числа $ρ$ и $φ$ (рис.), связанные с декартовыми прямоугольными координатами $x$ и $y$ формулами $x=ρ\cos φ$, $y=ρ\sin φ$, где $0⩽ρ<∞$, $0⩽φ<2π$. Координатные линии – концентрические окружности ($ρ=\rm{const}$) и лучи ($φ=\rm{const}$). Каждой точке плоскости $Oxy$ (за исключением точки $0$, для которой $ρ=0$, а $φ$ не определено, т. е. может быть любым числом $0⩽φ< 2π$) соответствует пара чисел ($ρ, φ$) и обратно. Расстояние $ρ$ от точки $M$ до точки $(0, 0)$ (полюса) называется полярным радиусом, а угол $φ$ – полярным углом. В полярных координатах элемент длины

$$dl=\sqrt{(dp)^2+ρ^2(dφ)^2},$$элемент площади

$$ds=ρdρdφ,$$оператор Лапласа

$$\Delta f=\frac{1}{ρ}\frac{\partial}{\partial ρ}\left( ρ\frac{\partial f}{\partial ρ}\right)+\frac{1}{ρ^2}\frac{\partial^2f}{\partial φ^2}.$$Обобщёнными полярными координатами называются числа $r$ и $ψ$, связанные с прямоугольными координатами формулами

$$x=ar \cos y, \,\,y=br\sin y,$$где $0⩽r<∞$, $0⩽ψ<2π$, $a>0$, $b>0$, $a≠b$. Координатные линии – эллипсы ($r=\rm{const}$) и лучи ($ψ=\rm{const}$). О полярной системе координат в пространстве см. в статье Сферическая система координат.

Полярная система координат в неявном виде использовал древнегреческий математик Динострат (4 в. до н. э.) при исследовании квадратрисы. Подобие полярной системы координат имеется у А. Дюрера (1525). И. Ньютон в «Методе флюксий» (1670–1671, опубликовано в 1736) трижды использовал полярную систему координат и привёл формулы, связывающие их с прямоугольными координатами. В почти современном виде полярная система координат появилась у Я. Бернулли (1691), чёткое представление об определении точки на плоскости при помощи полярной системы координат имелось у Л. Эйлера (1748). Термин «полярная система координат» возник в 19 в. К современным обозначениям полярных координат ближе всего обозначения Л. Эйлера: $z$, $φ$, а также С. Е. Гурьева: $r$, $ω$.