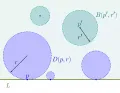
Пло́скость Немы́цкого, топологическое пространство, стандартный пример совершенного тихоновского пространства, не являющегося нормальным. Оно определяется следующим образом (см. рисунок). Множеством его точек является верхняя полуплоскость координатной плоскости, т. е. множество $P = \{(x,y)\in\mathbb {R}^2: y\geqslant 0 \}$. Пусть $L\subset P$ обозначает ось абсцисс [т. е. прямую, состоящую из всех точек вида $(a,0)$]; для каждой точки $p\in L$ и числа $r>0$ пусть $D(p,r)$ обозначает множество всех точек из $P$, лежащих внутри круга радиуса $r$, касающегося прямой $L$ в точке $p$. Другими словами, если $p=(a,0)$, то

$$D(p,r)=\left\{(x,y)\in P: (x-a)^2+(y-r)^2<r^2\right\}.$$Для точки $p'\in P$, не принадлежащей множеству $L$, и числа $r'>0$ пусть $B(p',r')$ обозначает множество точек полуплоскости $P$, лежащих в обычном открытом круге радиуса $r'$ с центром в $p$, т. е. если $p'=(a,b)$, где $b>0$, то

$$B(p',r')=\bigl\{(x,y)\in P: (x-a)^2+(y-b)^2<{r'}^2\,\bigr\}.$$Базой топологии на $P$ является, по определению, семейство, состоящее: а) из всех множеств вида $B(p',r')$, где $p'\in P\setminus L$ и $r'>0$; б) всех множеств вида $\{p\}\cup D(p,r)$, где $p\in L$ и $r>0$.

Основные свойства плоскости Немыцкого

1. Пусть $E$ обозначает топологическое пространство с тем же множеством точек, что и у плоскости Немыцкого $P$, но взятым с обычной топологией подпространства евклидовой плоскости. Тогда любое открытое в $E$ множество открыто и в $P$, т. е. топология плоскости Немыцкого является более сильной, чем обычная топология на верхней полуплоскости.

2. Подпространство $L$ замкнуто в $P$ и является дискретным пространством мощности континуума; топология на множестве $P\setminus L$ как подпространстве плоскости Немыцкого совпадает с обычной топологией подпространства евклидовой плоскости.

3. $P$ удовлетворяет первой аксиоме счётности, но не удовлетворяет второй (вес плоскости Немыцкого равен мощности континуума); при этом пространство $P$ удовлетворяет второй аксиоме счётности локально, т. е. у каждой его точки существует окрестность $G$, обладающая счётной базой (как подпространство пространства $P$).

4. $P$ является сепарабельным совершенным тихоновским пространством; при этом оно не является наследственно сепарабельным (плотность его подпространства $L$ равна мощности континуума).

5. $P$ не является локально компактным пространством.

6. $P$ не является линделёфовым пространством (как и всякое топологическое пространство, содержащее несчётное замкнутое дискретное подпространство).

7. $P$ не является нормальным пространством. В частности, множество $Q\subset L$, состоящее из всех точек точек вида $(x,0)$, где $x$ рационально, и множество $J=L\setminus Q$, состоящее из всех точек вида $(x,0)$, где $x$ иррационально, являются замкнутыми в $P$ непересекающимися множествами, которые не могут быть отделены окрестностями (т. е. не существует таких открытых в $P$ множеств $U, V$, что $Q\subset U$, $J\subset V$ и $U\cap V=\varnothing$). Это можно показать, опираясь на теорему Бэра о категории.

Утверждение о том, что $P$ не является нормальным, также следует из леммы Джоунса (см. видеолекцию).

Вместе с тем пространство $P$ можно дополнить одной точкой до нормального пространства; более точно: существует (хаусдорфово) нормальное пространство $X$, такое, что для некоторой точки $x\in X$ подпространство $X\setminus\{x\}$ гомеоморфно плоскости Немыцкого $P$.

8. Пространство $P$ вещественно полно.

9. Пространство $P$ полно по Чеху (и, следовательно, является пространством Бэра).

10. Из того, что пространство $P$ не нормально (а также из того, что оно сепарабельно, но имеет несчётный вес), следует его неметризуемость. При этом пространство $P$ является локально метризуемым (и даже локально метризуемым полной метрикой), т. е. каждая его точка обладает окрестностью $G$ (необязательно открытой), топология которой как подпространства пространства $P$ может быть задана некоторой полной метрикой на $G$.

11. Пространство $P$ не паракомпактно (поскольку оно не является нормальным) и даже не счётно паракомпактно.

12. В каждое счётное открытое покрытие $\mathcal{W}$ пространства $P$ можно вписать точечно конечное открытое покрытие, причём предположение о счётности $\mathcal{W}$ существенно. (Другими словами, $P$ счётно метакомпактно, но не метакомпактно.)

13. Пространство $P$ является пространством Мура.

Исторические и библиографические сведения

Плоскость Немыцкого была впервые определена (в качестве примера регулярного ненормального пространства) в монографии П. С. Александрова и Х. Хопфа «Topologie I» (Alexandroff. 1935) со ссылкой на В. В. Немыцкого. В США плоскость Немыцкого часто называют «плоскостью Мура» (последние десятилетия – с оговоркой: «также известной как плоскость Немыцкого»); это связано с тем, что Р. Л. Мур привёл плоскость Немыцкого в качестве простого примера регулярного неметризуемого пространства с измельчением (см., например, Vickery. 1940. P. 564).

Существуют различные модификации плоскости Немыцкого, представляющие собой важные примеры в общей топологии.

Плоскость Немыцкого. Видеолекция Алексея Зубова. 2023.Плоскость Немыцкого. Видеолекция Алексея Зубова. 2023.

Архив БРЭАрхив БРЭ