Дифференциа́л, главная линейная часть приращения функции.

1) Действительная функция $y=f(x)$ действительного переменного называется дифференцируемой в точке $x$, если она определена в некоторой окрестности этой точки и если существует такое число $A$, что приращение$$\Delta y = f (x + \Delta x) - f (x)$$$($при условии, что точка $x + \Delta x$ лежит в упомянутой окрестности$)$ может быть представлено в виде$$\Delta y = A \Delta x + \alpha,$$где $\alpha / \Delta x \rightarrow 0$ при $\Delta x\to0$. При этом $A \Delta x$ обозначается через $dy$ и называется дифференциалом функции $f(x)$ в точке $x$. Дифференциал $dy$ при фиксированном $x$ пропорционален $\Delta x$, т. е. является линейной функцией от $\Delta x$. Дополнительный член $\alpha$ при $\Delta x\to0$ является, в силу определения, бесконечно малой более высокого порядка по сравнению с $\Delta x$ $($и по сравнению с $dy$, если $A\neq0)$. Именно в этом смысле дифференциал и называется главной частью приращения функции.

Для функции, дифференцируемой в точке $x$, $\Delta y\to0$ при $\Delta x\to0$, т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция $f(x)$ дифференцируема в точке $x$ в том и только в том случае, если она имеет в этой точке конечную производную$$f ^ { \prime } (x) = \lim\limits _ {\Delta x \rightarrow 0 } \ \frac{\Delta y }{\Delta x }  = A ;$$при этом$$d y = f ^ { \prime } (x) \Delta x .$$Существуют непрерывные, но не дифференцируемые функции.

Кроме обозначения $dy$ используется обозначение $df(x)$; тогда предыдущее равенство принимает вид$$d f (x) = f ^ { \prime } (x) \Delta x .$$Приращение аргумента $\Delta x$ обозначается также через $dx$ и называется дифференциалом независимого переменного. Поэтому можно писать$$d y = f ^ { \prime } (x) d x .$$Отсюда $f ^ { \prime } (x) = dy / dx$, т. е. производная равна отношению дифференциалов $dy$ и $dx$. Если $A = 0$, то $\Delta y / dy \rightarrow 1$ при $\Delta x \rightarrow 0$, т. е. $\Delta y$ и $dy$ при $\Delta x \rightarrow 0$ являются в случае $A\neq0$ эквивалентными бесконечно малыми; этим, равно как и простой структурой дифференциала $($линейностью по $\Delta x)$, часто пользуются в приближённых вычислениях, полагая $\Delta y \approx dy$ при малых $\Delta x$. Если хотят, например, вычислить $f (x + \Delta x)$, зная $f(x)$ $(\Delta x$ мало$)$, то полагают$$f (x + \Delta x) \approx f(x) + dy .$$Конечно, такое рассуждение имеет ценность, если можно оценить соответствующую погрешность.

Геометрическое истолкование дифференциала. Уравнение касательной к графику функции $y=f(x)$ в точке $M(x_0, y_0)$ имеет вид $y — y _ {0} = f ^ { \prime } (x _ {0}) (x — x _ {0}).$ Если положить $x = x _ {0} + \Delta x$, то $y - y _ {0} = f ^ { \prime } (x _ {0}) \Delta x$. Правая часть есть значение дифференциала функции $f(x)$ в точке $x_0$, отвечающее рассматриваемому значению $\Delta x$. Таким образом, дифференциал совпадает с соответствующим приращением ординаты касательной к кривой $y=f(x)$ $($см. отрезок $NT$ на рис. 1$)$. При этом $\alpha=\Delta y-dy$, т. е. значение $|\alpha|$ совпадает с длиной отрезка $TS$.

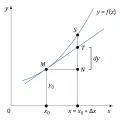Рис. 1.Рис. 1.

2) Определение дифференцируемости и дифференциала естественным образом обобщается на действительные функции от $n$ действительных переменных. Например, в случае $n=2$ действительная функция $z=f(x, y)$ называется дифференцируемой в точке $(x, y)$ по совокупности переменных $x$ и $y$, если она определена в некоторой окрестности этой точки и её полное приращение$$\Delta z = f (x + \Delta x , y + \Delta y) - f (x , y)$$может быть представлено в виде$$\Delta z = A \Delta x + B \Delta y + \alpha ,$$где $A$ и $B$ – некоторые числа, $\alpha / \rho \rightarrow 0$ при $\rho \rightarrow 0$, $\rho = \sqrt {\Delta x ^ {2} + \Delta y ^ {2} }$; предполагается,

что точка $(x + \Delta x , y + \Delta y)$ принадлежит упомянутой окрестности (см. рис. 2). 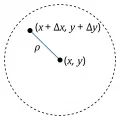Рис. 2.Рис. 2.При этом вводится обозначение$$d z = d f (x , y) = A \Delta x + B \Delta y$$и $dz$ называется полным дифференциалом, или просто дифференциалом, функции $f(x, y)$ в точке $(x, y)$ $($иногда с добавлением: «по совокупности переменных $x$ и $y$»$)$.

Для фиксированной точки $(x,y)$ дифференциал $dz$ есть линейная функция от $\Delta x$ и $\Delta y$; разность $\alpha= \Delta z-dz$ есть бесконечно малая более высокого порядка по сравнению с $\rho$. В этом смысле $dz$ есть главная линейная часть приращения $\Delta z$.

Если $f(x, y)$ дифференцируема в точке $(x, y)$, то она непрерывна в этой точке и имеет в ней конечные частные производные$$f _ {x} ^ { \prime } (x , y) = A ,\quad f _ {y} ^ { \prime } (x , y) = B.$$Таким образом,$$d z = d f (x , y) = f _ {x} ^ { \prime } (x , y) \Delta x + f _ {y} ^ { \prime } (x , y) \Delta y .$$Приращения $\Delta x$ и $\Delta y$ независимых переменных, как и в случае одного переменного, обозначаются $dx$ и $dy$. По этой причине можно написать$$d z = d f (x , y) = f _ {x} ^ { \prime } (x , y)  d x + f _ {y} ^ { \prime } (x , y) d y .$$Существование конечных частных производных, вообще говоря, не влечёт дифференцируемости функции (даже если предполагать заранее её непрерывность) – здесь нарушается аналогия с функциями одного переменного.

Если функция $f(x, y)$ имеет в точке $(x, y)$ частную производную по $x$, то произведение $f'_x(x, y)dx$ называется её частным дифференциалом по $x$; аналогично, $f'_y(x, y)dy$ есть частный дифференциал по $y$. Если функция дифференцируема, то её полный дифференциал равен сумме частных дифференциалов. Геометрически полный дифференциал $df (x _ {0} , y _ {0})$ есть приращение аппликаты касательной плоскости к поверхности $z=f(x, y)$ в точке $(x _ {0} , y _ {0} , z _ {0})$, где $z _ {0} = f (x _ {0} , y _ {0})$ (см. рис. 3).

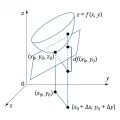Рис. 3.Рис. 3.Достаточный признак дифференцируемости функции: если в некоторой окрестности точки $(x_0,y_0)$ функция $f(x, y)$ имеет частную производную $f'_x$, непрерывную в точке $(x_0,y_0)$, и, кроме того, имеет в точке $(x_0,y_0)$ частную производную $f'_y$, то $f(x, y)$ дифференцируема в этой точке.

Если функция $f(x, y)$ дифференцируема в каждой точке открытой области $D$, то в любой точке этой области$$d z = A (x , y) d x + B (x , y) d y ,$$причём $A (x , y) = f _ {x} ^ { \prime } (x , y)$, $B (x , y) = f _ {y} ^ { \prime } (x , y)$. Если при этом существуют непрерывные в $D$ частные производные $A _ {y} ^ \prime$ и $B _ {x} ^ { \prime }$, то всюду$$A _ {y} ^ \prime = B _ {x} ^ { \prime } .$$Это показывает, в частности, что не всякое выражение$$A (x , y) d x + B (x , y) d y$$с непрерывными $A$ и $B$ $($в области $D)$ является в этой области полным дифференциалом некоторой функции двух переменных. В этом состоит ещё одно нарушение аналогии с функциями одного переменного, где любое выражение $A (x) d x$ с непрерывной в некотором промежутке функцией $A (x)$ служит дифференциалом для некоторой функции.

Выражение $A dx + B dy$ является полным дифференциалом некоторой функции $z=f(x, y)$, в односвязной открытой области $D$, если $A (x, y)$ и $B (x, y)$ непрерывны в этой области и удовлетворяют условию $A _ {y} ^ \prime = B _ {x} ^ { \prime }$ и при этом

а) $A _ {y} ^ \prime$ и $B _ {x} ^ { \prime }$ непрерывны или

б) $A (x, y)$ и $B (x, y)$ дифференцируемы по совокупности переменных $x$ и $y$ всюду в $D$ (Толстов. 1950; 1948).

О дифференциале действительных функций одного или нескольких действительных переменных и о дифференциалах высших порядков см. также Дифференциальное исчисление.

3) Пусть функция $f(x)$ определена на некотором множестве $E$ действительных чисел, $x$ – предельная точка этого множества, $x\in E$, $x+\Delta x\in E$, $\Delta y=A\Delta x+\alpha$, где $\alpha / \Delta x \rightarrow 0$ при $\Delta x\to 0$; тогда функция $f(x)$ называется дифференцируемой по множеству $E$ в точке $x$, a $dy=A\Delta x$ называется её дифференциалом по множеству $E$ в точке $x$. Это есть обобщение дифференциала действительной функции одного действительного переменного. Разновидностями этого обобщения являются дифференциалы в концах промежутка, на котором определена функция, и аппроксимативный дифференциал.

Подобным же образом вводится дифференциал по множеству для действительных функций многих действительных переменных.

4) Все эти определения дифференцируемости и дифференциала почти без изменений распространяются соответственно на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе они распространяются на функции точки абстрактного пространства. Можно говорить о дифференцируемости и дифференциале функции множества по отношению к некоторой мере.