Обра́тные тригонометри́ческие фу́нкции (аркфункции, круговые функции), функции, обратные тригонометрическим функциям. Значения обратных тригонометрических функций являются решением следующей задачи: найти число по заданному значению его тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть обратных тригонометрических функций: арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс (названия происходят от лат. arc – дуга), они обозначаются соответственно $\textrm{Arcsin}\,x,$ $\textrm{Arccos}\,x,$ $\textrm{Arctan}\,x,$ $\textrm{Arccot}\,x,$ $\textrm{Arcsec}\,x,$ $\textrm{Arccosec}\,x$ (две последние функции мало употребительны и далее не рассматриваются). Согласно этому определению, например, величина $y=\textrm{Arcsin}\,x$ есть решение уравнения $\sin y=x$, т. е. $y$ есть длина дуги, синус которой равен $x$, т. о., $\sin(\textrm{Arcsin}\,x)=x$. Поскольку тригонометрические функции периодичны, обратные к ним функции являются многозначными. Определённые однозначные ветви (главные ветви) обратных тригонометрических функций обозначаются $\arcsin x, \arccos x, \arctan x, \textrm{arccot}\,x$; их другие обозначения – $\sin^{–1}x, \cos^{–1}x, \tan^{–1}x, \cot^{–1}x$.

Впервые специальные символы для обратных тригонометрических функций использовал Д. Бернулли (1729, 1736), современные обозначения для обратных тригонометрических функций ввели в 1772 г. австрийский математик К. Шерфер и Ж. Лагранж.

Обратные тригонометрические функции действительного переменного  $\arcsin x, \arccos x, \arctg x, \arcctg x$ определяются как обратные к функциям $\sin x, \cos x, \tan x, \cot x$, заданным соответственно на промежутках $[-π/2, π/2], [0, π], (-π/2, π/2), (0, π)$. Т. о., равенство

$$y=\arcsin x$$означает, что $\sin y=x$ и $-π/2 \leqslant y \leqslant π/2:$

$$\{ y=\arcsin x \} ⇔ \{ \sin y=x, -π/2 \leqslant y \leqslant π/2 \}.$$Аналогично,

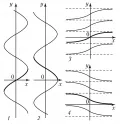
$$\{ y= \arccos x \} ⇔ \{ \cos y=x, 0 \leqslant y \leqslant π \}, \\ \{ y= \arctan x \} ⇔ \{ \tan y=x, -\pi/2 \lt y \lt \pi/2 \}, \\ \{y = \arctan x \} ⇔ \{\cot y=x, 0 \lt y \lt \pi \}.$$Эти обратные тригонометрические функции однозначны, непрерывны и их свойства вытекают из свойств тригонометрических функций (таблице 1). Значения обратных тригонометрических функций для некоторых значений аргумента приведены в таблицах 2 и 3. Графики обратных тригонометрических функций см. на рис. Обратные тригонометрические функции бесконечно дифференцируемы и в окрестности каждой внутренней точки своей области определения могут быть разложены в ряды Тейлора. Обратные тригонометрические функции связаны соотношениями:

$$\begin{aligned}\arcsin x+ \arccos x &= π/2,\quad -1\leqslant x \leqslant 1,\\ \arctan x + \textrm{arccot}\, x&=π/2,\quad -∞ \lt x \lt \infty,\end{aligned}$$поэтому функции $\arccos x$ и $\textrm{arccot}\,x$ в таблице 4 не фигурируют.

Для многозначных обратных тригонометрических функций справедливы равенства:

$$\begin{aligned}\textrm{Arcsin}\,x &= (-1)^n \arcsin x + \pi n, \\ \textrm{Arccos}\,x &= \pm \arccos x + 2\pi n, \\ \textrm{Arctan}\,x &= \arctan x + \pi n,\\ \textrm{Arccot}\,x &= \textrm{arccot}\,x +\pi n,\end{aligned}$$

где $n=0, ±1, ±2,\ldots\,$.

Обратные тригонометрические функции комплексного переменного $z=x+iy$ определяются как аналитические продолжения соответствующих обратных тригонометрических функций действительного переменного в комплексную плоскость. Они могут быть выражены через логарифмическую функцию $\textrm{Ln}\,z$:

$$\begin{aligned}\textrm{Arcsin}\,z&=-i \,\textrm{Ln}(z+\sqrt{1-z^2},\\ \textrm{Arccos}\,z &=-i\,\textrm{Ln}(z+\sqrt{z^2-1,}\\ \textrm{Arctan}\,z &=\frac{i}{2}\,\textrm{Ln}\frac{1-iz}{1+iz},\\ \textrm{Arccot}\,z &=\frac{i}{2}\,\textrm{Ln}\frac{z-i}{z+i}.\end{aligned}$$