Проекти́вная геоме́трия, раздел геометрии, изучающий проективные свойства фигур, т. е. те свойства, которые не меняются при проективных преобразованиях, например при центральном проектировании. Параллельность и перпендикулярность прямых, равенство отрезков и углов суть непроективные свойства, поскольку пересекающиеся прямые могут

спроектироваться в параллельные, равные отрезки – в неравные и т. д. На рис. 1 показано

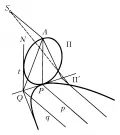Рис. 1. Пример центрального проектирования.Рис. 1. Пример центрального проектирования.центральное проектирование из точки $S$ окружности, которая лежит в плоскости $П$, на плоскость $П'$: пересекающиеся прямые $AQ$ и $AP$ проектируются в параллельные прямые $p$ и $q$, окружность проектируется в параболу, касательная $QN$ к окружности проектируется в касательную к параболе. Проективными свойствами являются, например, расположение точек на одной прямой (коллинеарность), гармоническое расположение точек на прямой (см. Двойное отношение), порядок и класс алгебраической кривой, касание прямой и любой линии, разделённость (см. ниже).

При проектировании точек одной плоскости на другую не каждая точка плоскости $П$ имеет образ на плоскости $П'$ и не каждая точка $П'$ имеет прообраз на $П$. Это обстоятельство привело к необходимости присоединения к евклидовой плоскости т. н. бесконечно удалённых (несобственных) точек. Такое присоединение приводит к понятию проективной плоскости. Евклидова плоскость, дополненная несобственными элементами, называется действительной проективной плоскостью. На ней через любые две различные точки проходит (и притом только одна) прямая, и любые две различные прямые имеют (и притом только одну) общую точку. Дополнение евклидовой плоскости до проективной приводит к тому, что проектирование становится взаимно однозначным преобразованием. Аналогичным образом из евклидова пространства получается проективное пространство.

Аксиоматическое задание действительной проективной плоскости может быть осуществлено различными способами. Наиболее распространённая система аксиом получается видоизменением системы аксиом, предложенной Д. Гильбертом для обоснования евклидовой геометрии на плоскости. Проективная плоскость рассматривается как совокупность элементов двух родов: точек и прямых, между которыми устанавливаются отношения инцидентности и порядка, характеризуемые соответствующими аксиомами. Эта группа аксиом отличается от соответствующей группы аксиом евклидовой геометрии тем, что каждые две прямые на

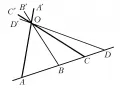Рис. 2. Точки и прямые на проективной плоскости.Рис. 2. Точки и прямые на проективной плоскости.плоскости имеют общую точку и что на прямой имеются по крайней мере три различные точки. В качестве основного отношения порядка принимается разделённость двух пар точек, лежащих на одной прямой, или двух пар прямых, проходящих через одну точку. На рис. 2 пара точек $A$ и $C$ разделяет пару точек $B$ и $D$, пара прямых $AA'$ и $CC'$ разделяет пару прямых $BB'$ и $DD'$. Разделённость также описывается своей системой аксиом. Иногда к этим аксиомам добавляются аксиомы непрерывности.

Существуют интерпретации проективной плоскости, не привлекающие бесконечно удалённых элементов. Например, пусть $E^3$ – евклидово пространство и $O$ – точка в нём. Обозначим через $П$ множество прямых, проходящих через $O$; точкой в $П$ назовём евклидову прямую, проходящую через $O$, а прямой в $П$– множество евклидовых прямых, проходящих через $O$ и лежащих в одной плоскости. Тогда $П$ удовлетворяет аксиомам проективной плоскости.

Большое значение в проективной геометрии имеет принцип двойственности. Основные понятия проективной плоскости – точка и прямая связаны между собой также одним из основных понятий проективной геометрии – инцидентностью. Точка и прямая инцидентны, если точка принадлежит прямой или (что то же самое) прямая проходит через точку. Принцип двойственности утверждает, что если верно какое-либо предложение, касающееся точек, прямых и отношения инцидентности между ними, то верно и т. н. двойственное предложение, получаемое из данного, если поменять слова «прямая» и «точка» (для проективного пространства слова «плоскость» и «точка»). Например, двойственны предложения:

• двум различным точкам инцидентна прямая (и притом только одна);

• двум различным прямым инцидентна точка (и притом только одна).

Принцип двойственности отражает фундаментальное свойство проективной плоскости: прямые и точки на ней – равноправные геометрические объекты.

Важную роль в проективной геометрии играет предложение Дезарга. В частности, его выполнение необходимо и достаточно для введения координат на проективной плоскости проективными средствами.

Основы проективной геометрии заложены в 17 в. Ж. Дезаргом (в связи с развитием учения о перспективе) и Б. Паскалем (в связи с изучением некоторых свойств конических сечений). Большое значение для последующего развития проективной геометрии имели работы Г. Монжа. Как самостоятельная дисциплина проективная геометрия была изложена Ж.-В. Понселе (начало 19 в.). Заслуга Понселе заключалась в выделении проективных свойств фигур в отдельный класс и установлении соответствий между метрическими и проективными свойствами фигур. К этому же периоду относятся работы французского математика Ш. Брианшона. Дальнейшее развитие проективная геометрия получила в работах швейцарского математика Я. Штейнера и французского математика М. Шаля. Большую роль в развитии проективной геометрии сыграли работы немецкого математика К. Штаудта, которыми были также намечены контуры аксиоматического построения проективной геометрии. Все эти геометры стремились доказывать теоремы проективной геометрии синтетическим методом, положив в основу изложения проективные свойства фигур. Аналитическое направление в проективной геометрии было намечено работами А. Мёбиуса. Влияние на развитие проективной геометрии оказали работы Н. И. Лобачевского по созданию неевклидовой геометрии, позволившие в дальнейшем А. Кэли и Ф. Клейну рассмотреть различные геометрические системы с точки зрения проективной геометрии.

Некоторые положения и факты проективной геометрии применяются в теории статистических решений, в квантовой теории поля, в конструировании печатных схем (через теорию графов).