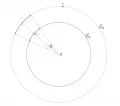
Двойна́я окру́жность Алекса́ндрова, топологическое пространство, классический пример компактного хаусдорфова пространства, удовлетворяющего первой аксиоме счётности, но не удовлетворяющего второй. Оно строится следующим образом (см. рис.). Пусть $C_1$ и $C_2$ – две несовпадающие концентрические окружности на плоскости, а $p\colon C_1\to C_2$ – отображение проектирования окружности $C_1$ на окружность $C_2$ из их общего центра $o$. (Другими словами, если $z\in C_1$, то $p(z)$ есть точка пересечения луча $oz$ с окружностью $C_2$.) Для каждой точки $z\in C_1$ пусть $V(z,\alpha)$ обозначает открытую дугу окружности $C_1$ с угловой величиной $\alpha$ (где $0<\alpha<2\pi$) и с серединой в точке $z$. На множестве $A=C_1\cup C_2$ определяется топология: база её открытых множеств состоит из а) всех одноточечных множеств вида $\{c\}$, где $c\in C_2$ (т. е. все точки окружности $C_2$ объявляются изолированными); б) множеств вида $$U(z,\alpha) = V(z,\alpha)\cup p\left(V(z,\alpha)\setminus \{z\}\right)$$при всевозможных $z\in C_1$ и $0<\alpha<2\pi$; таким образом, для каждой точки $z\in C_1$ семейство $\{U(z,\alpha):0<\alpha<2\pi\}$ есть семейство базисных окрестностей точки $z$.

Построенное топологическое пространство $A$ (не зависящее, с точностью до гомеоморфизма, от радиусов окружностей $C_1$ и $C_2$) и называется двойной окружностью Александрова. Это пространство компактно и хаусдорфово; топология подпространства $C_1\subset A$ совпадает с обычной топологией окружности как подпространства евклидовой плоскости (т. е. подпространство $C_1$ гомеоморфно одномерной сфере $\mathbb{S}^1$), а подпространство $C_2\subset A$ дискретно, открыто и всюду плотно в $A$ – таким образом, $A$ является компактификацией дискретного пространства мощности континуума.

Пространство $A$ удовлетворяет первой аксиоме счётности, но не удовлетворяет второй; оно даже не сепарабельно, так как содержит открытое дискретное подпространство $C_2$ мощности континуума. Кроме того, $A$ наследственно нормально, но не совершенно нормально (его открытое подмножество $C_2$ не является $F_{\sigma}$-множеством) – отсюда (а также из того, что оно компактно, но не удовлетворяет второй аксиоме счётности) следует его неметризуемость.

В основе построения двойной окружности Александрова лежит общетопологическая конструкция, которая состоит в следующем. Пусть $X$ – произвольное топологическое пространство; положим $A(X)=X\cup X_0$, где $X_0$ – некоторая копия множества $X$, не пересекающаяся с ним, т. е. такое множество $X_0$, что $X\cap X_0=\varnothing$, и существует биекция $p\colon X\to X_0$. На множестве $A(X)$ определим топологию, выбирая в качестве базы открытых множеств все одноточечные множества вида $\{c\}$, где $c\in X_0$ и все множества вида $V\cup p(V\setminus \{z\})$, где $z\in X$ и $V$ – открытое в $X$ множество, содержащее точку $z$. Так построенное пространство $A(X)$ называется александровским удвоением (или удвоением по Александрову) пространства $X$. Двойная окружность Александрова представляет собой частный случай александровского удвоения – а именно, является александровским удвоением окружности (одномерной сферы).

Для того чтобы пространство $A(X)$ было компактным (хаусдорфовым, тихоновским, нормальным), необходимо и достаточно, чтобы пространство $X$ обладало соответствующим свойством.

Двойная окружность Александрова была определена в «Мемуаре о компактных топологических пространствах» П. С. Александрова и П. С. Урысона (Alexandroff. 1929; русский перевод: Александров. 1971. С. 30–32). Конструкция александровского удвоения была введена Р. Энгелькингом (Engelking. 1968).