Структурная нейтронография
Структу́рная нейтроногра́фия, экспериментальный метод исследования атомной структуры конденсированных сред с помощью упругого когерентного рассеяния (дифракции) нейтронов низких энергий (< 0,5 эВ) на атомных ядрах. Метод во многом аналогичен рентгеновскому структурному анализу, но имеет многочисленные особенности, определяемые спецификой взаимодействия нейтронов со средой, и, как правило, применяется, если решение структурной задачи с помощью рассеяния рентгеновских лучей связано с большими трудностями или вообще невозможно. Наиболее общей задачей исследования структуры вещества на атомном уровне с помощью дифракции нейтронов является извлечение информации о распределении когерентной длины рассеяния из экспериментально измеренной интенсивности рассеянного излучения, связанных соотношением:
Здесь – вектор рассеяния, и – волновые векторы нейтрона до и после рассеяния, – амплитуда рассеянной волны, r – координата точки внутри объекта, на котором происходит рассеяние нейтрона. Возможность анализа атомной структуры с использованием дифракции нейтронов обеспечивает их сильное взаимодействие с атомными ядрами. Соответственно, входящие в (1) длины рассеяния, , в структурной нейтронографии относятся к рассеянию на ядрах атомов. Магнитное дипольное взаимодействие магнитных моментов нейтрона и электронов атома, выступающее как дополнительное к ядерному, обеспечивает возможность анализа магнитной структуры кристаллов с использованием дифракции нейтронов и относится к магнитной нейтронографии. При дифракции нейтрона на кристалле обмен кинетической энергией происходит между налетающим нейтроном и всем кристаллом, величина переданной энергии очень мала (относительное изменение энергии нейтрона по порядку величины составляет отношение масс нейтрона и кристалла), следовательно, где λ – его длина волны де Бройля, и для модуля вектора рассеяния можно получить: где θ – половина угла рассеяния.
Основными объектами, изучаемыми в рамках структурной нейтронографии, являются кристаллические вещества, т. е. твёрдые тела, обладающие упорядоченной трёхмерно-периодической пространственной атомной структурой (тела с дальним порядком). В этом случае возможно максимально полное решение структурной задачи – определение положений всех атомов в элементарной ячейке кристалла. Если ядерное, когерентное рассеяние нейтронов происходит на веществе, не имеющем дальнего порядка в расположении атомов (жидкости, аморфные среды), то возможно определение некоторых статистических характеристик структуры, которые извлекаются из корреляционных функций, измеряемых в эксперименте по рассеянию нейтронов.
Основными разделами структурной нейтронографии являются кристаллография, дифракция нейтронов и структурный анализ. Первый раздел включает сведения о трансляционной симметрии кристаллов, их внутренней (пространственной) симметрии, групповых свойствах элементов симметрии и обратной решётке кристалла. Второй раздел включает основы нейтронной физики, формализм дифракции излучения на периодических структурах, специфику дифракции нейтронов на кристаллах и экспериментальную реализацию метода. Предметом структурного анализа являются математические методы получения структурной информации из измеренных дифракционных спектров, среди которых анализ Фурье, теория групп, параметрическая минимизация функционалов.
Отличия нейтронографии от других структурных методов, использующих коротковолновое излучение (рентгеновских и синхротронных лучей, электронов), в основном связаны с физической природой и свойствами длин рассеяния, входящих в (1), но, кроме того, и с некоторыми методическими особенностями организации структурного эксперимента. К первым в первую очередь относится нерегулярность зависимости от номера элемента и массового числа ядра. Ко вторым – возможность сканирования обратного пространства кристалла с использованием метода времени пролёта.
Историческая справка
Первые физические исследования дифракции нейтронов на кристаллах были выполнены под руководством Э. Ферми в 1947 г. с нейтронами, выведенными из тепловой колонны ядерного реактора в Аргоннской лаборатории (США).  Рис. 1. Первая демонстрация нейтронных дифракционных изотопических эффектов при замене водорода на дейтерий. Репродукция графиков из статьи: Shull C. G. [et al.]. Neutron Diffraction Studies of NaH and NaD // The Physical Review. 1948. Vol. 73, № 8. P. 842–847. Перевод: БРЭ.Систематические исследования, которые уже можно отнести к структурной нейтронографии, были начаты в 1948 г. на ядерном реакторе в Ок-Риджской национальной лаборатории (США), имевшем мощность около 3 МВт, где на одном из выведенных пучков нейтронов был сооружён первый двухосный нейтронный дифрактометр с монохроматическим пучком нейтронов. В том же году появилась обзорная статья [1], в которой приведено описание конструкции дифрактометра, даны краткие теоретические сведения, включая формулу для интегральной интенсивности дифракционного пика, рассмотрены изотопические и спиновые эффекты, опубликованы первые нейтронограммы. На этом дифрактометре были выполнены классические работы К. Шалла, связанные с наблюдением изотопических эффектов в (рис. 1) и подтверждением гипотезы о существовании антиферромагнитного упорядочения в кристаллах MnO, которые в будущем послужили основанием для присуждения ему Нобелевской премии (совместно с Б. Брокхаузом) в 1994 г.
Рис. 1. Первая демонстрация нейтронных дифракционных изотопических эффектов при замене водорода на дейтерий. Репродукция графиков из статьи: Shull C. G. [et al.]. Neutron Diffraction Studies of NaH and NaD // The Physical Review. 1948. Vol. 73, № 8. P. 842–847. Перевод: БРЭ.Систематические исследования, которые уже можно отнести к структурной нейтронографии, были начаты в 1948 г. на ядерном реакторе в Ок-Риджской национальной лаборатории (США), имевшем мощность около 3 МВт, где на одном из выведенных пучков нейтронов был сооружён первый двухосный нейтронный дифрактометр с монохроматическим пучком нейтронов. В том же году появилась обзорная статья [1], в которой приведено описание конструкции дифрактометра, даны краткие теоретические сведения, включая формулу для интегральной интенсивности дифракционного пика, рассмотрены изотопические и спиновые эффекты, опубликованы первые нейтронограммы. На этом дифрактометре были выполнены классические работы К. Шалла, связанные с наблюдением изотопических эффектов в (рис. 1) и подтверждением гипотезы о существовании антиферромагнитного упорядочения в кристаллах MnO, которые в будущем послужили основанием для присуждения ему Нобелевской премии (совместно с Б. Брокхаузом) в 1994 г.
В России систематическое развитие структурной нейтронографии началось в конце 1950-х гг. на стационарных ядерных реакторах в Курчатовском институте и Институте теоретической и экспериментальной физики (Москва) и в Петербургском институте ядерной физики (ПИЯФ, Гатчина), где были сооружены классические двухосные дифрактометры.  Рис. 2. Руслан Озеров (справа) с профессором Хартмутом Фуссом (Германия) во время школы по нейтронной физике. Дубна. 1982.В середине 1960-х гг. нейтронные дифракционные эксперименты стали проводиться на первом в мире импульсном ядерном реакторе (Импульсный Быстрый Реактор, ИБР) в Объединённом институте ядерных исследований (ОИЯИ, Дубна) с использованием метода времени пролёта. Подробные описания основных этапов развития дифракции нейтронов в мире даны в юбилейном сборнике статей Дж. Бэкона и в историческом обзоре Р. П. Озерова, который (рис. 2) по праву считается одним из основоположников развития структурной нейтронографии в СССР. Под его руководством были выполнены первые структурные исследования на реакторе в Курчатовском институте. В последующем именно Р. П. Озеров стал основным соавтором и редактором 3-томника «Нейтроны и твёрдое тело», содержащем основные сведения по нейтронографии.
Рис. 2. Руслан Озеров (справа) с профессором Хартмутом Фуссом (Германия) во время школы по нейтронной физике. Дубна. 1982.В середине 1960-х гг. нейтронные дифракционные эксперименты стали проводиться на первом в мире импульсном ядерном реакторе (Импульсный Быстрый Реактор, ИБР) в Объединённом институте ядерных исследований (ОИЯИ, Дубна) с использованием метода времени пролёта. Подробные описания основных этапов развития дифракции нейтронов в мире даны в юбилейном сборнике статей Дж. Бэкона и в историческом обзоре Р. П. Озерова, который (рис. 2) по праву считается одним из основоположников развития структурной нейтронографии в СССР. Под его руководством были выполнены первые структурные исследования на реакторе в Курчатовском институте. В последующем именно Р. П. Озеров стал основным соавтором и редактором 3-томника «Нейтроны и твёрдое тело», содержащем основные сведения по нейтронографии.
Основные формулы
При рассмотрении дифракции на кристаллах интегрирование в (1) можно заменить на суммирование по атомам в одной элементарной ячейке кристалла и по всем элементарным ячейкам в кристалле, что приводит к формуле для интенсивности:
где – структурный фактор элементарной ячейки, – вектор трансляции в обратной решётке кристалла. В (2) δ-функция Дирака возникла вследствие предположения о бесконечных размерах кристалла по всем направлениям. Её присутствие означает, что сечение когерентного рассеяния и, следовательно, дифракционная интенсивность рассеяния отличны от нуля, только если То, что в этой точке сечение формально обращается в бесконечность, связано со сделанными в ходе расчёта приближениями. Ориентация вектора в обратном пространстве определяется направлениями первичного, , и дифрагированного, , пучков. Ориентация вектора задаётся направлениями базисных векторов элементарной ячейки кристалла. Их связь определяет геометрию дифракционного эксперимента с монокристаллом. Переход к модулям векторов и приводит к уравнению Брэгга-Вульфа, где – набор межплоскостных расстояний в кристалле, величины которых определяются параметрами элементарной ячейки и индексами Миллера – угол Брэгга, равный половине угла рассеяния. Это уравнение используется для расчёта положений дифракционных пиков на оси углов рассеяния или длин волн, если эксперимент ведётся с поликристаллом.
Строгая формула для интенсивности получается при квантово-механическом подходе к задаче о дифракции нейтронов на совокупности рассеивающих центров (объекте), при котором решается уравнение Шрёдингера с заданным потенциалом взаимодействия. В стандартном варианте эта задача решается в рамках первого борновского приближения со специальным видом потенциала, получившим название «псевдопотенциал Ферми» (предложен Э. Ферми в 1936). Это даёт возможность получить дифференциальное сечение упругого рассеяния т. е. вероятность того, что нейтрон будет рассеян в элемент телесного угла без изменения энергетических состояний кристалла и нейтрона. Такой расчёт позволяет получить точный числовой коэффициент в выражении для дифракционной интенсивности и учесть влияние теплового движения атомов.
Действия по извлечению нейтронной структурной информации об объекте из формулы (2) в случае изучения монокристалла аналогичны тем, которые выполняются в случае использования рентгеновских лучей. А именно, проводится интегрирование по в некоторой окрестности узлов обратной решётки, в полученную (интегральную) интенсивность вносятся необходимые поправки на поглощение и экстинкцию нейтронов в образце и учитывается способ сканирования узлов решётки. Это даёт возможность определить структурные факторы элементарной ячейки:
где – когерентная длина рассеяния j-го атома, находящегося в положении , суммирование идет по всем атомам в ячейке или по некоторой их части, если учитываются симметрийные законы погасания, фактор учитывает тепловые колебания атомов возле положений равновесия (фактор Дебая – Уоллера). Структурный фактор является рядом Фурье по отношению к величинам b'j = bj∙exp(-Wj), и можно выполнить обратное преобразование Фурье, что даёт:
где уже рассматривается как непрерывная функция в объёме элементарной ячейки, – дискретный набор векторов обратной решётки кристалла, – любой вектор в элементарной ячейке, сумма по является тройной суммой по , по и по , каждая из которых должна быть вычислена в пределах Реально суммирование выполняется в некоторых пределах для каждой из переменных Функция представляет собой набор максимумов в объёме элементарной ячейки, их положения совпадают с положениями ядер атомов, их величины пропорциональны длинам рассеяния , их ширины определяются разрешением в кристаллическом пространстве и факторами Дебая – Уоллера. Анализ функции – величин и координат её максимумов – позволяет определить тип и координаты атомов структуры. Величины в ряде (4) в общем случае являются комплексными, и для его вычисления необходимо знать модули и фазы структурных факторов.  Рис. 3. Фурье-синтез нейтронной рассеивающей плотности HgBa₂CuO₄.₁ в сечении элементарной ячейки, выполненный по экспериментальным структурным факторам. Иллюстрация из статьи: Балагуров А. М. [и др.]. Нейтронографические исследования зависимости атомной структуры высокотемпературных ртутных сверхпроводников от анионного состава и внешнего давления // Физика элементарных частиц и атомного ядра. 2004. Т. 35. С. 1357.Из (2) следует, что в стандартном дифракционном эксперименте может быть получена информация о модулях, но не о фазах структурных факторов (фазовая проблема структурного анализа). В случае рентгеноструктурного анализа имеется несколько методов решения фазовой проблемы, но практика структурной нейтронографии показала, что для неё фактически ни один из известных методов не является эффективным в достаточной степени. Поэтому стандартным подходом является определение модели структуры в рентгеновском эксперименте, расчёт по ней приблизительных фаз нейтронных структурных факторов и их последующее уточнение с использованием данных, полученных в нейтронном эксперименте. Именно такая последовательность действий была выполнена при нейтронографическом уточнении структуры высокотемпературного сверхпроводника Рентгеновский структурный анализ не обеспечивал нужной точности в определении положения и количества сверхстехиометрического кислорода из-за присутствия тяжёлых атомов ртути. Построение карт нейтронной рассеивающей плотности (их принято называть фурье-синтезами) позволило это сделать (рис. 3).
Рис. 3. Фурье-синтез нейтронной рассеивающей плотности HgBa₂CuO₄.₁ в сечении элементарной ячейки, выполненный по экспериментальным структурным факторам. Иллюстрация из статьи: Балагуров А. М. [и др.]. Нейтронографические исследования зависимости атомной структуры высокотемпературных ртутных сверхпроводников от анионного состава и внешнего давления // Физика элементарных частиц и атомного ядра. 2004. Т. 35. С. 1357.Из (2) следует, что в стандартном дифракционном эксперименте может быть получена информация о модулях, но не о фазах структурных факторов (фазовая проблема структурного анализа). В случае рентгеноструктурного анализа имеется несколько методов решения фазовой проблемы, но практика структурной нейтронографии показала, что для неё фактически ни один из известных методов не является эффективным в достаточной степени. Поэтому стандартным подходом является определение модели структуры в рентгеновском эксперименте, расчёт по ней приблизительных фаз нейтронных структурных факторов и их последующее уточнение с использованием данных, полученных в нейтронном эксперименте. Именно такая последовательность действий была выполнена при нейтронографическом уточнении структуры высокотемпературного сверхпроводника Рентгеновский структурный анализ не обеспечивал нужной точности в определении положения и количества сверхстехиометрического кислорода из-за присутствия тяжёлых атомов ртути. Построение карт нейтронной рассеивающей плотности (их принято называть фурье-синтезами) позволило это сделать (рис. 3).
В случае дифракции на поликристалле вместо измерения интегральных интенсивностей отдельных дифракционных пиков, перевода их в структурные факторы и построения карт рассеивающей плотности проводится анализ профиля нейтронограммы, измеренной в широком интервале углов рассеяния или длин волн. Вводя функцию , описывающую профиль дифракционного пика, для интенсивности можно получить следующее общее выражение:
где – некоторая константа (в неё входят время измерения, объём кристалла и др.), – межплоскостное расстояние, – поток нейтронов на образце, – фактор повторяемости кристаллографической плоскости, – фактор Лоренца. Здесь учтены ещё фактор поглощения, и коэффициент экстинкции, зависящие от угла рассеяния и длины волны нейтрона. В (5) интенсивность спектра записана как функция межплоскостного расстояния, хотя в качестве переменной можно использовать угол рассеяния или время пролёта. Конкретное выражение для фактора Лоренца зависит от типа дифрактометра, на котором проведено измерение спектра.
Метод анализа профиля нейтронограммы ввел в общую практику голландский физик Х. Ритвельд (H. Rietveld) в конце 1960-х гг., а с 1978 г. он получил официальное (рекомендованное Международным союзом кристаллографов) название – метод Ритвельда. В этом методе предполагается, что измеряемый профиль дифракционного спектра может быть описан аналитической функцией, зависящей от экспериментальных и структурных переменных. Кроме того, считается, что начальные значения структурных параметров (факторов заполнения позиции, относительных координат и характеристик теплового движения атомов) уже известны с достаточной точностью и речь идет только об их уточнении с помощью метода наименьших квадратов или каких-либо других процедур минимизации функционалов. Результат обработки представляется в виде графика, включающего в числе прочего разностную функцию, иногда нормированную на статистическую ошибку (рис. 4). Основой эффективности метода Ритвельда является то, что удаётся описать профили дифракционных пиков в широком диапазоне переменной относительно простыми аналитическими функциями с небольшим количеством свободных параметров и, кроме того, в нем достигается наименьший уровень корреляции между параметрами. Метод Ритвельда хорошо приспособлен для алгоритмизации, и доступен целый ряд удобных компьютерных программ, его реализующих.
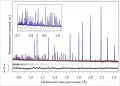 Рис. 4. Дифракционный спектр минерала Na₂Al₂Ca₃F₁₄, измеренный на дифрактометре HRFD (реактор ИБР-2 Объединённого института ядерных исследований) и обработанный по методу Ритвельда. Показаны экспериментальные точки, рассчитанная кривая и разностная функция, нормированная на ошибку в точке. Штрихи указывают расчётные положения пиков основной фазы. В спектре присутствуют пики от небольшого количества примесной фазы CaF₂. Иллюстрация из статьи: Балагуров А. М. [и др.]. Корреляционная фурье-дифрактометрия: 20-летний опыт эксплуатации на реакторе ИБР-2 // Физика элементарных частиц и атомного ядра. 2015. Т. 46. С. 473.Основной экспериментальной задачей при изучении структуры жидкостей и аморфных веществ (сред без дальнего порядка) является как можно более точное определение парной радиальной функции распределения которая связана с вероятностью обнаружения частицы в точке если одна из частиц находится в начале координат. Из рассмотрения, основанного на методах квантовой механики, следует, что для изотропного ансамбля одинаковых рассеивающих центров (одноатомная жидкость) их радиальное распределение может быть связано с функцией которая является интегралом от закона рассеяния (предварительно усреднённого по ориентациям) по всем переданным энергиям:
Рис. 4. Дифракционный спектр минерала Na₂Al₂Ca₃F₁₄, измеренный на дифрактометре HRFD (реактор ИБР-2 Объединённого института ядерных исследований) и обработанный по методу Ритвельда. Показаны экспериментальные точки, рассчитанная кривая и разностная функция, нормированная на ошибку в точке. Штрихи указывают расчётные положения пиков основной фазы. В спектре присутствуют пики от небольшого количества примесной фазы CaF₂. Иллюстрация из статьи: Балагуров А. М. [и др.]. Корреляционная фурье-дифрактометрия: 20-летний опыт эксплуатации на реакторе ИБР-2 // Физика элементарных частиц и атомного ядра. 2015. Т. 46. С. 473.Основной экспериментальной задачей при изучении структуры жидкостей и аморфных веществ (сред без дальнего порядка) является как можно более точное определение парной радиальной функции распределения которая связана с вероятностью обнаружения частицы в точке если одна из частиц находится в начале координат. Из рассмотрения, основанного на методах квантовой механики, следует, что для изотропного ансамбля одинаковых рассеивающих центров (одноатомная жидкость) их радиальное распределение может быть связано с функцией которая является интегралом от закона рассеяния (предварительно усреднённого по ориентациям) по всем переданным энергиям:
где
В общем случае изучаются двух- и многокомпонентные системы, анализ дифракционных спектров от которых позволяет извлечь данные о парциальных распределениях, т. е. о функциях типа которые определяют число атомов компоненты на расстоянии r от некоторого атома компоненты Для повышения точности анализа зачастую используется изотопическое контрастирование, что возможно только в структурной нейтронографии.
Задачи структурной нейтронографии
Формулы (2) – (6) имеют общий характер и не зависят от вида излучения, специфика которого проявляется в физической сути величин . Ядерные когерентные длины рассеяния нейтронов имеют ряд особенностей, важных с точки зрения структурного анализа. Одна из них – независимость от угла рассеяния и (для большинства изотопов) от длины волны нейтрона, т. е. эти величины являются некоторыми константами и не уменьшаются при увеличении переданного импульса как атомные формфакторы рассеяния рентгеновских лучей. Соответственно, интенсивности дифракционных пиков могут быть измерены с хорошей статистикой в широком диапазоне , и при прочих равных условиях разрешение фурье-синтезов, построенных по нейтронным данным, обычно лучше, чем в случае рентгеновского структурного анализа. Ещё одна их особенность – отсутствие знаковой определённости, имеющейся при анализе дифракции рентгеновских лучей. В отдельных случаях, например при анализе водородосодержащих структур, это обстоятельство повышает его точность, т. к. когерентная длина рассеяния водорода отрицательна и резко контрастирует с плотностью распределения других атомов. Нерегулярность зависимости bj от номера элемента и массового числа ядра позволяет проводить прецизионный структурный анализ соединений, содержащих и лёгкие, и тяжёлые атомы (гидридов, оксидов), и анализ соединений, содержащих элементы с близкими атомными номерами (интерметаллидов, сплавов). Кроме того, появляется возможность выделения отдельных фрагментов структуры путём внедрения специально подобранных изотопов (изотопическое контрастирование).
Помимо классической проблемы получения информации о статической атомной структуре кристаллов или жидкостей, в рамках структурной нейтронографии решается множество специальных задач, требующих нестандартной организации эксперимента и особых методов анализа данных. Одна из наиболее распространённых задач такого рода – анализ необратимых переходных процессов in situ и в реальном времени, примерами которых являются химические твердотельные реакции, изотопный обмен, структурные фазовые переходы. Необходимое условие для реализации таких исследований – высокая светосила дифрактометра. Достигнутые на некоторых источниках потоки нейтронов и прогресс в создании детекторов с большим телесным углом позволяют набирать достаточную статистику за время порядка 1 мин, что даёт возможность детального анализа переходных процессов, имеющих характерные времена ~5 мин и больше. На рис. 5 показано, как изменяются дифракционные спектры (измерения проведены на дифрактометре HRFD, реактор ИБР-2) в ходе структурных фазовых переходов в сплаве Fe-27Ga при его медленном нагреве. Последующий анализ интенсивностей пиков и их зависимости от температуры (или от времени) позволяет получить подробную структурную информацию о возникающих фазах, роде переходов между ними, эволюции микроструктуры сплава и т. д.
 Рис. 5. Эволюция дифракционных спектров сплава Fe-27Ga в ходе его нагрева со скоростью 2 град/мин до 950 °С. Изменения спектров соответствуют переходам между различными структурными фазами: D0₃ → L1₂ → D0₁₉ → A2. Указаны индексы Миллера дифракционных пиков. Иллюстрация из статьи: Golovin I. S. [et al.]. In situ neutron diffraction study of bulk phase transitions in Fe-27Ga alloys // Materials & Design. 2016. Vol. 98. P. 113–119. Перевод: БРЭ.Как особые разделы в рамках структурной нейтронографии принято выделять исследования локальных искажений структуры кристаллов (метод PDF), анализ длиннопериодных и несоизмеримо модулированных структур, исследования с экстремальными внешними воздействиями на образец (высокое давление, электрическое или магнитное поле), анализ микроструктуры кристаллов (уровень микронапряжений, характерные размеры областей когерентного рассеяния и их морфология и др.).
Рис. 5. Эволюция дифракционных спектров сплава Fe-27Ga в ходе его нагрева со скоростью 2 град/мин до 950 °С. Изменения спектров соответствуют переходам между различными структурными фазами: D0₃ → L1₂ → D0₁₉ → A2. Указаны индексы Миллера дифракционных пиков. Иллюстрация из статьи: Golovin I. S. [et al.]. In situ neutron diffraction study of bulk phase transitions in Fe-27Ga alloys // Materials & Design. 2016. Vol. 98. P. 113–119. Перевод: БРЭ.Как особые разделы в рамках структурной нейтронографии принято выделять исследования локальных искажений структуры кристаллов (метод PDF), анализ длиннопериодных и несоизмеримо модулированных структур, исследования с экстремальными внешними воздействиями на образец (высокое давление, электрическое или магнитное поле), анализ микроструктуры кристаллов (уровень микронапряжений, характерные размеры областей когерентного рассеяния и их морфология и др.).
Для решения прикладных задач в структурной нейтронографии широко используется высокая проникающая способность нейтронов (~3 см в стали) и относительно большое (~1 см2) поперечное сечение пучка, что даёт возможность получения информации, усреднённой по объёму образца, и позволяет избежать неопределённостей, связанных с крупнокристаллической или неоднородной структурой материалов и с поверхностными эффектами. Эти свойства особенно важны при изучении внутренних остаточных напряжений в объёмных телах и изделиях и при анализе текстуры сплавов и минералов.
Экспериментальная техника
Эксперименты в рамках структурной нейтронографии проводятся на обоих существующих типах исследовательских источников – стационарных и импульсных. На стационарных источниках с постоянным во времени потоком для экспериментов используется монохроматический ) пучок нейтронов. Структурные исследования монокристаллов ведутся на двухосных дифрактометрах, оборудованных, как правило, двухкоординатным позиционно-чувствительным детектором (2D ПЧД). Современная детекторная система дифрактометра для поликристаллов – широкоапертурный ПЧД, охватывающий несколько десятков градусов по углу рассеяния.
Относительно небольшая скорость нейтронов низких энергий (~2000 м/с) позволяет эффективно использовать метод времени пролёта (МВП) для определения их энергии (длины волны). Первые полноценные дифракционные эксперименты с использованием этого метода были проведены в начале 1960-х гг. на импульсном реакторе ИБР в ОИЯИ (Дубна), что послужило катализатором последующего его бурного развития на других типах импульсных источников нейтронов – электронных и протонных ускорителях с мишенью из тяжёлого металла. В 1990-х гг. был сделан ещё один знаковый шаг в развитии дифракции нейтронов с использованием МВП. На импульсном реакторе ИБР-2 был создан (в коллаборации с ПИЯФ, Гатчина и VTT, Espoo, Финляндия) дифрактометр HRFD с быстрым фурье-прерывателем и корреляционным методом набора данных, что позволило значительно (в ~15 раз) улучшить разрешение по межплоскостному расстоянию [4]. Основное достоинство МВП – возможность использования почти всего сплошного (полихроматического или «белого») спектра нейтронов от источника, тогда как на обычных дифрактометрах с монохроматическим пучком доля «полезных» нейтронов составляет около 1 %. В результате, несмотря на то что средняя по времени мощность импульсных источников существенно меньше мощности стационарных ядерных реакторов (в 10 и более раз), с точки зрения дифракционного эксперимента их эффективности сравнимы.
Дифрактометры с монохроматическим или с «белым» спектром позволяют решать однотипные задачи с примерно одинаковым успехом, хотя некоторые варианты экспериментов могут быть реализованы только на дифрактометрах по времени пролёта. Например, на нём можно проводить набор данных от кристалла, помещенного в ячейку высокого давления, при фиксированном угле рассеяния. Кроме того, дифрактометр по времени пролёта, оборудованный двухкоординатным позиционно-чувствительным детектором (2D ПЧД), даёт уникальную возможность проведения трёхмерного сканирования обратного пространства монокристалла без каких-либо его поворотов. Но, с другой стороны, прецизионность структурной информации, как правило, более высокая при использовании дифрактометра с постоянной длиной волны. В целом оба типа нейтронных дифрактометров рассматриваются как взаимодополняющие, и для решения сложных структурных задач их следует использовать параллельно.
Исключительное разнообразие нейтронных дифракционных задач привело к необходимости специализации конструкции дифрактометров и их оптимизации по какому-то параметру (светосиле, разрешению, уровню фона) или по его настройке на работу в определённом интервале длин волн. К 2020-м гг. в структурной нейтронографии используется около 10 разных типов дифрактометров со специфической организацией основных узлов и подбором параметров (см. Таблицу; под обычным или большим диапазоном понимаются интервалы 0,7 – 5 Å или 0,5 – 15 Å соответственно).
Задача | Светосила | Разрешение, Δd/d | Диапазон, dhkl | Детектор |
Атомная структура, монокристалл | Средняя | Среднее, ~0,02 | Обычный | 2D ПЧД |
Атомная структура, поликристалл | Средняя | Высокое, ~0,002 | Большой | Большой 1D ПЧД |
Структура жидкостей, аморфных тел | Средняя | Среднее, ~0,02 | Малые λ, Qmax ~ 20 Å–1 | Большой 1D ПЧД |
Эксперимент в реальном времени | Высокая | Среднее, ~0.02 | Большой | Большой 1D ПЧД |
Высокое внешнее давление | Высокая, малый фон | Среднее, ~0,02 | Обычный | Большой 1D ПЧД |
Длиннопериодные структуры | Средняя | Среднее, ~0,02 | Большие dhkl | 2D ПЧД на малых углах |
Локальные искажения структуры | Высокая | Высокое, ~0,004 | Малые λ, Qmax ~ 40 Å–1 | Большой 1D ПЧД |
Макронапряжения в материалах | Высокая | Высокое, ~0,004 | Обычный | 2D ПЧД при 2θ ≈ 90º |
Микроструктура материалов | Средняя | Высокое, ~0,002 | Большой | Большой 1D ПЧД |
Кристаллографическая текстура | Средняя | Высокое, ~0,004 | Большой | 2D ПЧД |
