Магни́тная нейтроногра́фия, экспериментальный метод исследования магнитной структуры конденсированных сред с помощью упругого когерентного рассеяния (дифракции) нейтронов низких энергий (< 0.5 эВ) при взаимодействии магнитных моментов нейтрона и атома. Под исследованием магнитной структуры подразумевается определение её типа, симметрии и периодов упорядочения моментов, их величины и ориентации относительно друг друга и относительно кристаллографических осей. Как и при исследовании атомной структуры с помощью дифракции нейтронов, необходимым условием для полного решения этой задачи является наличие дальнего магнитного порядка, т. е. какой-либо закономерности в величинах и направлениях магнитных моментов атомов на расстояниях ~100 нм и больше. В кристалле, находящемся в парамагнитном состоянии или в состоянии спинового стекла, дальний порядок в направлениях моментов отсутствует. В этом случае возможно определение некоторых статистических характеристик, извлекаемых из данных по корреляциям взаимных направлений магнитных моментов.

В кристаллах с упорядоченными моментами выделяют тип коллинеарных магнетиков, к которым относят ферро- (ФМ), антиферро- (АФМ) и ферримагнитные (ФРМ) состояния. Для этих типов магнитных состояний может быть определена элементарная магнитная ячейка, которая либо совпадает с кристаллической, либо превышает её (для АФМ и ФРМ структур) в целое число раз по одной, двум или по всем трём осям. Существует много вариантов неколлинеарных магнетиков, в которых магнитные моменты упорядочены некоторым сложным образом – например, по сторонам треугольника, по нескольким непараллельным направлениям и т. д. Наконец, имеются структуры, у которых периоды упорядочения величины или направления магнитных моментов несоизмеримы с периодами кристаллической решётки. В этом случае структуру называют несоизмеримо модулированной, в ней невозможно выделить элементарную магнитную ячейку. Помимо магнитных структур в магнитную нейтронографию иногда включаются изучение динамики магнитных моментов атомов, рефлектометрическое отражение нейтронов под малыми углами и магнитное малоугловое рассеяние нейтронов.

Магнитная нейтронография фактически является единственным прямым методом определения магнитной структуры кристаллов. Важная дополнительная информация может быть получена с помощью некоторых других микроскопических методов: рассеяния и поглощения синхротронного излучения, μSR- и γ-резонансной спектроскопии.

Историческая справка

Первый эксперимент, в котором наблюдалась магнитная дифракция нейтронов, был проведён в 1949 г. на ядерном реакторе в Ок-Риджской национальной лаборатории (США), на сооружённом там первом двухосном нейтронном дифрактометре с монохроматическим пучком нейтронов. Рис. 1. Дифракционные спектры от поликристалла MnO, измеренные при комнатной температуре (внизу) и T = 80 K (вверху). При переходе из парамагнитной в антиферромагнитную фазу при 120 K элементарная ячейка увеличивается в размерах и появляются новые дифракционные пики. Иллюстрация из публикации: Shull C. G., Smart J. S. Detection of antiferromagnetism by neutron diffraction // Physical Review. 1949. Vol. 76, № 8. P. 1256.Рис. 1. Дифракционные спектры от поликристалла MnO, измеренные при комнатной температуре (внизу) и T = 80 K (вверху). При переходе из парамагнитной в антиферромагнитную фазу при 120 K элементарная ячейка увеличивается в размерах и появляются новые дифракционные пики. Иллюстрация из публикации: Shull C. G., Smart J. S. Detection of antiferromagnetism by neutron diffraction // Physical Review. 1949. Vol. 76, № 8. P. 1256.На нём удалось подтвердить гипотезу о существовании антиферромагнитного упорядочения в кристаллах $MnO$ (рис. 1). Одному из авторов работы (К. Шаллу) за этот и многие другие важные результаты, полученные с помощью дифракции нейтронов, в 1994 г. была присуждена (совместно с Б. Брокхаузом) Нобелевская премия.

В России магнитная нейтронография развивалась начиная с 1960-х гг., в основном сотрудниками Петербургского института ядерной физики (Гатчина) и Института физики металлов (ИФМ, Екатеринбург) на стационарных ядерных реакторах ВВР-М и ИВВ-2М соответственно. Юрий Александрович Изюмов. 2004.Юрий Александрович Изюмов. 2004.В 1970-х гг. на импульсном ядерном реакторе ИБР в Объединённом институте ядерных исследований (Дубна) были начаты дифракционные эксперименты по влиянию сильных импульсных магнитных полей на поведение АФМ структур. Тогда же в ИФМ под руководством С. В. Вонсовского начались углублённые теоретические исследования магнетизма. Сотрудниками этого института (Ю. А. Изюмов, В. Е. Найш) были выполнены основополагающие работы по теории рассеяния нейтронов на кристаллах с упорядоченной магнитной структурой и по использованию теории групп для анализа магнитных структур. Ю. А. Изюмов стал основным соавтором монографий, до сих пор являющихся настольными руководствами для специалистов по магнитной нейтронографии.

Основные формулы

Задача о рассеянии нейтронов при их взаимодействии с магнитными моментами атомов является квантовомеханической. Для её решения используется релятивистское уравнение Дирака с заданным потенциалом взаимодействия. Для нейтрона, являющегося фермионом, потенциал взаимодействия с электромагнитным полем электронов атома – многокомпонентный, в частности, он включает взаимодействия Фолди и Швингера. Но главный вклад в магнитное рассеяние вносит взаимодействие магнитного момента нейтрона со спиновым и орбитальным моментами атома. Если магнитные моменты атомов не упорядочены по направлениям (в случае парамагнетика), то магнитное упругое рассеяние представляет собой некогерентный фон со специфической зависимостью интенсивности от вектора рассеяния, а именно – сечение рассеяния неполяризованных нейтронов в этом случае есть:

$$d σ /d Ω = 2 / 3(r_0γ)^2 S(S + 1)P^2(\boldsymbol{Q}), \tag1$$где r₀ = e²/m_ec² = 2.818·10^-13 см – классический радиус электрона, е – заряд электрона, m_e – масса электрона, с – скорость света, γ = -1.9132 – аномальный магнитный момент нейтрона (в ядерных магнетонах), $S$ – спин атома (в единицах ħ), $P(\boldsymbol{Q})$ – магнитный формфактор атома (фурье-преобразование распределения спиновой плотности электронов), $\boldsymbol{Q} = \boldsymbol{k_1} – \boldsymbol{k_0}$ – вектор рассеяния, $\boldsymbol{k_0}$ и $\boldsymbol{k_1}$ – волновые векторы нейтрона до и после рассеяния. Магнитный формфактор $P(\boldsymbol{Q})$ имеет форму, близкую к гауссовой, т. е. интенсивность некогерентного парамагнитного рассеяния максимальна при малых величинах вектора рассеяния и плавно спадает с ростом Q. Физическая причина появления в формулах для магнитного рассеяния формфактора – соизмеримость длины волны нейтрона и размеров электронного облака атома, что приводит к конструктивной интерференции волн, рассеянных в различных точках облака.

Когерентное магнитное рассеяние (дифракция) возникает, если магнитные моменты атомов кристалла каким-либо образом упорядочены по направлениям и по величине. В этом случае квантовомеханический расчёт позволяет определить матричный элемент [подробный вывод приведён в (Изюмов. 1966)], с помощью которого могут быть вычислен магнитный структурный фактор F_M и далее – дифференциальное сечение рассеяния, определяющее магнитный вклад в интенсивности дифракционных пиков. При вычислении интенсивности рассеяния для магнитных структур с определённой элементарной ячейкой так же как в случае анализа кристаллической структуры, производится суммирование по атомам в одной ячейке и по всем элементарным ячейкам в кристалле, что приводит к

$$I(\boldsymbol{Q})  \sim |FM(\boldsymbol{H})|^2  δ (\boldsymbol{Q} – 2 π \boldsymbol{H}), \tag2$$где $\boldsymbol{H}$ – вектор трансляции в обратной решётке кристалла. В (2) дельта-функция Дирака возникла вследствие предположения о бесконечных размерах кристалла по всем направлениям. Её присутствие означает, что дифракционная интенсивность рассеяния отлична от нуля только при $\boldsymbol{Q} = 2 π\boldsymbol{H}$. Если магнитная и кристаллическая элементарные ячейки совпадают, как, например, в случае ФМ структуры, то интенсивности дифракционных пиков определяются обоими вкладами – ядерным и магнитным. Если магнитная элементарная ячейка больше кристаллической, как, например, в случае одноатомной АФМ структуры, то необходимо переопределить вектор трансляции, добавив к нему вектор магнитной структуры $\boldsymbol{K}$ (обычно называемый вектором распространения): $\boldsymbol{H = H_N + K}$. В этой формуле $\boldsymbol{H_N}$ – векторы трансляции в кристаллической обратной решётке, а вектор распространения находится из связи направлений моментов какого-либо исходного атома в «0»-ячейке и атома в n-й (кристаллографической) ячейке:

$$\boldsymbol{S}_n = \boldsymbol{S}_0 • exp(2 π i\boldsymbol{KT}_n),  \tag3$$где $\boldsymbol{T_n}$ - векторы трансляции, связывающие нулевую и n-ю ячейки, набор которых включает и векторы центрирующих ячейку узлов. Для ФМ структуры $\boldsymbol{K} = 0,$ т. е. все моменты направлены одинаково. АФМ чередование направления моментов вдоль какого-либо базисного направления (условие $\boldsymbol{S_n = –S_0}$ при n нечётном) задаётся вектором типа $\boldsymbol{K} = (1/2,0,0)$ , чередование вдоль обоих направлений в плоскости или по всем трём базисным направлениям задается векторами типа $\boldsymbol{K} = (1/2,1/2,0)$ или $\boldsymbol{K} = (1/2,1/2,1/2)$, соответственно. Таким образом, при K ≠ 0 в обратном пространстве появляются дополнительные узлы, имеющие нецелочисленные индексы Миллера, если индексация ведётся в кристаллографической ячейке.

Ситуация несколько усложняется в случае несоизмеримо модулированной магнитной структуры. Например, в случае структуры с двумя векторами распространения $\boldsymbol{K}$ и $-\boldsymbol{K}$ формула (3) заменяется на

$$\boldsymbol{S}_n = \boldsymbol{S}_0 • exp(2 π i\boldsymbol{KT}_n) + \boldsymbol{S}_0* • exp(–2 π i\boldsymbol{KT}_n),    \tag4$$где $\boldsymbol{T_n}$ – как и ранее, векторы трансляции, связывающие 0-ю и n-ю ячейки, причём вектор $\boldsymbol{S_0}$, задающий ориентацию магнитного момента в 0-й ячейке, в общем случае может быть комплексным, как, например, при описании спиральной магнитной структуры. Рис. 2. Пример проявления сателлитных пиков.Рис. 2. Пример проявления сателлитных пиков.Синусоидальная модуляция величины или направления момента с периодом много большим периода кристаллической ячейки приводит к появлению т. н. сателлитов, располагающихся рядом с основными пиками (рис. 2). Если модуляция какого-либо параметра негармоническая, то рядом с основными пиками появляются несколько сателлитов с постепенно уменьшающимися амплитудами.

Параллельный учёт ядерного и магнитного взаимодействий приводит к выражениям для интенсивности вида: $I \sim |FN±FM|^2$ , где F_N и F_M – атомный и магнитный структурные факторы. Появление знака ± связано с двумя возможными взаимными ориентациями магнитных моментов нейтрона и атома. Если обе ориентации равновероятны (неполяризованный пучок нейтронов), то при усреднении интерференционный член F_N•F_M исчезает и ядерный и магнитный вклады в интенсивности дифракционных пиков складываются, т. е. $I \sim |F_N|^2+F_M|^2.$ Общий вид магнитного структурного фактора в целом такой же, как у атомного, а именно:

$$F_M(\boldsymbol{H}) = |\boldsymbol{M}_{hkl}| \sum_j^N S_jf_jexp(2 π i\boldsymbol{Hr}_j)exp(–W_j),  \tag5$$где величину $\boldsymbol{M_{hkl}}$ принято называть вектором магнитного взаимодействия, $S_j$и $f_j$– спин и амплитуда магнитного рассеяния j-го атома, находящегося в положении ${r_j}$; суммирование идёт по всем магнитным атомам в ячейке или по некоторой их части, если учитываются симметрийные законы погасания, фактор exp(–W_j) учитывает тепловые колебания атомов возле положений равновесия (фактор Дебая–Валлера). Величина фактора |M_hkl| зависит от геометрии рассеяния, а именно – от взаимной ориентации двух единичных векторов: m, направленного вдоль магнитного момента атома, и $\boldsymbol{e} = \boldsymbol{Q}/Q = \boldsymbol{H}/H$, направленного вдоль вектора рассеяния:

$$|\boldsymbol{M}_{hkl}| = |m–\boldsymbol{e}(\boldsymbol{me})| = |sin η |, \tag6$$где $\eta$ – угол между векторами m и e. Амплитуда магнитного рассеяния определяется мировыми константами и магнитным формфактором конкретного атома: $f_j = e^2γ/(m_ec^2)∙P_j(Q)$. Подстановка констант приводит к $f_j = 5.39P_j(Q)·10^{-13} см$, что при малых Q сравнимо по величине с когерентными длинами ядерного рассеяния. Конкретные выражения для магнитного структурного фактора в общем случае неколлинеарной структуры зависят от её типа и могут иметь более сложный вид, чем (5).

Структурный фактор $FM(\boldsymbol{H})$ является рядом Фурье по отношению к величинам $μ_j = S_jf_j∙exp(-W_j)$, и, выполняя обратное преобразование Фурье, можно получить распределение магнитной плотности $\mu$(r) как непрерывную функцию в объёме магнитной элементарной ячейки. Для проведения вычислений необходимо знать модули и фазы структурных факторов. Как и в случае анализа кристаллической структуры, модули определяются из магнитных вкладов в интенсивности дифракционных пиков, а фазы рассчитываются по модели магнитной структуры с последующим уточнением. Как правило, необходимая точность расчётов достигается, если набор экспериментальной информации производится на монокристалле с использованием поляризованного пучка нейтронов.

В случае дифракции на поликристалле вместо измерения интегральных интенсивностей отдельных дифракционных пиков, перевода их в структурные факторы и построения карт магнитной плотности проводится анализ профиля нейтронограммы, измеренной в широком интервале углов рассеяния или длин волн – с использованием метода Ритвельда. Вводя функцию $\varphi$, описывающую профиль дифракционного пика, для интенсивности можно получить следующее общее выражение:

$$I(d) = C • Ф(d) \sum_{hkl} ​ j_{hkl} • L • (|F_N(\boldsymbol{H}_{hkl})|^2 + |F_M(\boldsymbol{H}_{hkl})|^2 ) A( θ , λ ) • y( θ , λ ) • φ (d_{hkl} – d), \tag7$$где C – некоторая константа (в неё входят время измерения, объём кристалла и др.), d – межплоскостное расстояние, Ф – поток нейтронов на образце,$j_{hkl}$ – фактор повторяемости кристаллографической плоскости, L – фактор Лоренца. Здесь учтены фактор поглощения, A($\theta$,$\lambda$), и коэффициент экстинкции, y($\theta$,$\lambda$), зависящие от угла рассеяния и длины волны нейтрона. В (7) интенсивность спектра записана как функция межплоскостного расстояния, хотя в качестве переменной можно использовать угол рассеяния или время пролёта. Конкретное выражение для фактора Лоренца зависит от типа дифрактометра, на котором проведён эксперимент. Метод анализа профиля нейтронных дифракционных спектров ввёл в общую практику голландский физик Х. Ритвельд в конце 1960-х гг. именно для анализа магнитных структур (Rietveld. 1969). Впоследствии этот метод был распространён на анализ кристаллических структур и спектров, измеренных на рентгеновских или синхротронных дифрактометрах. Метод основан на минимизации разности экспериментальных и рассчитанных по модели интенсивностей с помощью метода наименьших квадратов или каких-либо других процедур минимизации функционалов. Параметрами магнитной структуры, по которым проводится минимизация, являются величины магнитных моментов и углы, определяющие их ориентацию относительно осей элементарной ячейки. Результат обработки представляется в виде графика, включающего в том числе разностную функцию, иногда нормированную на статистическую ошибку. Пример обработки для оксида NiO, находящегося в упорядоченном АФМ состоянии, приведён на рис. 3. Рис. 3. Обработанный по методу Ритвельда спектр от образца NiO, измеренного при 5 К (дифрактометр HRFD, реактор ИБР-2, ОИЯИ). Показаны экспериментальные точки, рассчитанная функция и разностная кривая, нормированная на ошибку в точке. Штрихи указывают положения кристаллических (верхний ряд) и магнитных (нижний ряд) пиков. Индексы Миллера приведены для ромбоэдрической пространственной группы с параметрами a = 2.9465 Å, α = 60.09°. На вставке показано ромбоэдрическое расщепление пиков, возникающее при формировании упорядоченной магнитной структуры.Рис. 3. Обработанный по методу Ритвельда спектр от образца NiO, измеренного при 5 К (дифрактометр HRFD, реактор ИБР-2, ОИЯИ). Показаны экспериментальные точки, рассчитанная функция и разностная кривая, нормированная на ошибку в точке. Штрихи указывают положения кристаллических (верхний ряд) и магнитных (нижний ряд) пиков. Индексы Миллера приведены для ромбоэдрической пространственной группы с параметрами a = 2.9465 Å, α = 60.09°. На вставке показано ромбоэдрическое расщепление пиков, возникающее при формировании упорядоченной магнитной структуры.Основой эффективности метода Ритвельда является то, что он позволяет описать профили дифракционных пиков в широком диапазоне переменной относительно простыми аналитическими функциями с небольшим количеством свободных параметров и, кроме того, в нём достигается наименьший уровень корреляции между параметрами. Метод Ритвельда хорошо приспособлен для алгоритмизации, и доступен целый ряд удобных компьютерных программ, реализующих его.

Анализ магнитной структуры

Возможны несколько вариантов анализа магнитной структуры. В случае если её тип и основные характеристики уже известны из предыдущих экспериментов, задача, как правило, сводится к уточнению каких-либо конкретных параметров: величины магнитных моментов, температуры перехода в упорядоченное состояние, зависимости упорядоченного момента от температуры и др. Для этого наиболее адекватным является использование метода Ритвельда. Если магнитная структура неизвестна, то её анализ включает несколько этапов. Для начала определяются или уточняются характеристики кристаллической структуры: пространственная группа, параметры элементарной ячейки, координаты и факторы заполнения кристаллографических позиций, факторы Дебая-Валлера. Затем определяются места магнитных вкладов в обратном пространстве в виде отдельных пиков или как дополнительной интенсивности в кристаллические пики. Эта процедура позволяет узнать вектор (или векторы) распространения магнитной структуры и сформулировать возможные модели структуры. Наконец, на заключительном этапе проводится анализ интенсивностей магнитных пиков или магнитного вклада в кристаллические пики для определения величин и направлений магнитных моментов атомов. Для этого используется метод Ритвельда, с помощью которого проверяется соответствие предложенных моделей и экспериментальных данных.

Для формулировки моделей структуры используются два подхода, один из которых основан на группах симметрии, другой – на теории неприводимых представлений. Симметрийное описание магнитных структур проводится в рамках групп антисимметрии, в которых к обычным геометрическим операциям симметрии добавлена операция изменения направления магнитного момента атома на противоположное. Добавление операции антисимметрии к пространственным (фёдоровским) группам симметрии рассмотрел в 1950-х гг. А. В. Шубников, который с её помощью производил смену цвета фигуры с белого на чёрный. Впоследствии эти группы симметрии получили название чёрно-белых, или шубниковских. Введение дополнительной операции симметрии приводит к увеличению числа возможных комбинаций: число трансляционных групп (кристаллических решёток) увеличивается с 14 до 36, число точечных групп – с 32 до 122, число пространственных групп – с 230 до 1651. Особенность, которую необходимо учитывать при симметрийном описании магнитных структур, состоит в том, что магнитный момент является аксиальным вектором и некоторые операции симметрии (например, зеркальное отражение) действуют на него не так, как на полярные векторы.

Альтернативный подход описания магнитной структуры кристаллов, основанный на теории неприводимых представлений (НП) пространственных кристаллографических групп, был предложен французским учёным Е. Берто (1968), а до рабочих алгоритмов доведён в работах российских физиков под руководством Ю. А. Изюмова (1980). В этом методе вводится разложение вектора магнитного момента по базисным функциям НП пространственной (фёдоровской) группы симметрии структуры кристалла. Поскольку НП, по которому прошёл фазовый переход с упорядочением магнитных моментов, заранее неизвестно, все возможные варианты проверяются в вариационной процедуре. Коэффициентов разложения по базисным функциям НП обычно немного (от 1 до 6), что способствует нахождению единственного решения.

Оба подхода реализованы в ряде компьютерных программ, находящихся в свободном доступе (GSAS-II, FullProf). Современное изложение основ магнитной нейтронографии можно найти в учебных пособиях Пирогова и Аксёнова.

Экспериментальная техника

Нейтронные дифракционные эксперименты по изучению магнитных структур проводятся на обоих существующих типах исследовательских источников – стационарных и импульсных. Исследования монокристаллов ведутся на двухосных дифрактометрах, оборудованных, как правило, двухкоординатным позиционно-чувствительным детектором, с использованием поляризованного пучка нейтронов. Дифрактометры для поликристаллов оборудуются широкоапертурными детекторами, охватывающими десятки градусов по углу рассеяния. В целом постановка «магнитного» нейтронного дифракционного эксперимента несколько отличается от «структурного». Учитывается, что магнитные формфакторы $P(\boldsymbol{Q})$ довольно быстро спадают с ростом Q. Соответственно, дифракционные пики с магнитным вкладом измеряются либо при сравнительно малых углах рассеяния, либо при сравнительно больших длинах волн. Поскольку в области малых Q дифракционные пики от поликристалла расположены редко, очень высокое разрешение, как правило, не требуется. В этом смысле дифрактометр, оптимизированный для изучения магнитной структуры, является дополнительным по своим параметрам к дифрактометру, оптимизированному для изучения атомной структуры. Как правило, измерения дифракционных спектров от магнитных кристаллов проводятся в широком диапазоне температур, что позволяет определить точки фазовых переходов и температурную зависимость величины упорядоченного магнитного момента, вектора распространения и других характеристик упорядоченной магнитной структуры, важных для понимания природы её возникновения. Кроме того, измерение спектров при температурах выше и ниже точки магнитного фазового перехода и вычитание их друг из друга является удобным методом выявления дифракционных пиков, имеющих магнитный вклад в интенсивность (рис. 4).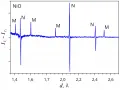Рис. 4. Результат вычитания двух нейтронограмм NiO, измеренных при температурах ниже (в магнитной фазе) и выше точки перехода. Хорошо видны одиночные магнитные дифракционные пики (M). Пики без магнитного вклада (N) состоят из положительной и отрицательной компонент, образовавшихся из-за температурного сдвига положений исходных пиков.Рис. 4. Результат вычитания двух нейтронограмм NiO, измеренных при температурах ниже (в магнитной фазе) и выше точки перехода. Хорошо видны одиночные магнитные дифракционные пики (M). Пики без магнитного вклада (N) состоят из положительной и отрицательной компонент, образовавшихся из-за температурного сдвига положений исходных пиков.

Дифракция нейтронов позволяет получить весьма полную информацию о магнитной структуре кристалла, но с помощью некоторых других микроскопических методов (рассеяния и поглощения синхротронного излучения, μSR- и γ-резонансной спектроскопии) удаётся узнать важные дополнительные детали. Например, на основе синхротронных данных можно выделить спиновый и орбитальный вклады в полный магнитный момент атома и выявить локальные пространственные флуктуации величины магнитного момента. μSR-метод даёт возможность раздельного определения величины магнитного момента и доли объёма образца, занятой упорядоченной магнитной фазой. Кроме того, методы μSR- и γ-резонансная спектроскопии обладают другой, по сравнению с методом дифракции нейтронов, чувствительностью к динамическим флуктуациям ориентации или величины магнитных моментов, что позволяет оценить характерное время сохранения определённого магнитного порядка в кристалле.