Симме́трия криста́ллов, свойство кристаллов самосовмещаться при поворотах, отражениях, параллельных переносах или комбинации этих операций; способность геометрических тел повторять свои части либо закономерное расположение объектов в пространстве (определение российского кристаллографа Е. С. Фёдорова). Симметрия кристаллов – предмет изучения геометрической кристаллографии, которая подразделяется на макро- и микрокристаллографию. Первая изучает конечные геометрические объекты (кристаллы), вторая – бесконечные периодические кристаллические структуры (внутреннее строение кристаллического вещества).

Точечные группы симметрии

Макрокристаллография изучает кристаллические многогранники как симметричные геометрические объекты, т. е. фигуры, которые могут самосовмещаться определёнными преобразованиями – поворотами, отражениями и др. Эти преобразования называются операциями симметрии. Геометрические образы, с помощью которых задаются или осуществляются операции симметрии, называются элементами симметрии. Симметрию любого кристалла можно описать точечной группой симметрии, которая является совокупностью всех существующих в данном кристалле элементов симметрии. Последние пересекаются в одной точке, которая не размножается ни одним элементом симметрии (остаётся неподвижной). Отсюда и название таких групп – точечные. В точечных группах могут встречаться следующие элементы симметрии: поворотные ($L_n$, $C_n$, или $n$), инверсионные ($Ł_n$, или $\bar{n}$) или зеркально-поворотные ($L_n$, или $S_n$) оси, плоскости зеркального отражения ($Р$, $\sigma$, или $m$) и центр инверсии (симметрии) ($С$, $i$, или$\bar{1}$).

При действии осей симметрии $L_n$ грани кристалла совмещаются с тождественными им путём поворота на угол $α$ (минимальный угол поворота, приводящего фигуру к самосовмещению), определяемый порядком оси $n = 360/α$ (рис. 1, а). Следовательно, порядок оси равен числу самосовмещений объекта при полном повороте на 360°. 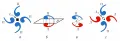Рис. 1. Действие на ассиметричный объект: а – поворотной оси 4-го порядка; б – плоскости симметрии; в – центра симметрии; г – инверсионной оси 4-го порядка. «Правые» и «левые» фигуры показаны различным цветом. БРЭ. Т. 30.Рис. 1. Действие на ассиметричный объект: а – поворотной оси 4-го порядка; б – плоскости симметрии; в – центра симметрии; г – инверсионной оси 4-го порядка. «Правые» и «левые» фигуры показаны различным цветом. БРЭ. Т. 30.Плоскости $Р$ связывают объекты, которые относятся друг к другу как предмет и его зеркальное отражение (рис. 1, б). Отражение в центре инверсии $С$ – аналогично оптической схеме фотоаппарата: объект отражается в фокусе и переворачивается (рис. 1, в). Инверсионные и зеркально-поворотные оси совмещают одновременный поворот и отражение, первые – в точке инверсии, вторые – в плоскости (рис. 1, г). Так, например, куб имеет: три оси 4-го порядка, которые проходят через центры противоположных граней, четыре оси 3-го порядка, проходящие по пространственным диагоналям куба, шесть осей 2-го порядка, проходящих через середины пар противоположных рёбер; девять плоскостей симметрии, три из которых взаимно перпендикулярны и делят пополам противоположные рёбра куба как координатные плоскости прямоугольной системы координат, а шесть плоскостей проходят по диагоналям граней куба; центр инверсии. Все элементы симметрии куба пересекаются в одной точке – в центре куба (центр инверсии). Точечная группа симметрии куба – $3L_44L_36L_29PC$ в первой систематической символике Браве (ныне устаревшей учебной), $m$ `$\bar{3} m$ (в международной символике, или символике Германа – Могена), или $O_h$ (в символике Шёнфлиса).

Реже встречающаяся в наши дни символика Шубникова основана на знании огранки кристаллов. Кристалл может ограняться как одинаковыми по симметрии гранями, так и различными. В этой связи в геометрической кристаллографии было введено понятие простой формы кристалла как совокупности граней, связанных между собой симметрическими операциями класса симметрии. Отметим, что грани, принадлежащие одной простой форме, равны по своим физическим свойствам. Для идеальных кристаллов они равны также и геометрически – т. е. обладают одинаковой формой и площадью поверхности. Согласно Шубникову класс называется по форме общего положения, которая располагается произвольно относительно элементов симметрии; в этом случае она является характеристической для выбранного класса, передавая ему свое название.

Точечные группы описывают симметрию не только кристаллов, но и молекул и любых конечных фигур. В отличие от других геометрических фигур и природных объектов, в кристаллах невозможны оси 5-го порядка и оси порядков выше 6-го. Это объясняется внутренним периодическим строением кристалла и связано с тем, что пятиугольниками и $n$-угольниками с $n > 6$ невозможно заполнить всё двумерное пространство без промежутков и перекрытий. Однако, в отличие от кристаллов, такие оси присутствуют в живых организмах (цветы, медузы и др.), а также в квазикристаллах, лишённых трёхмерного трансляционного периодического строения.

Число точечных групп симметрии бесконечно. Их принято делить на группы 1-го и 2-го рода. Первые содержат только простые поворотные оси и описывают кристаллы, состоящие только из совместимо равных частей. Группы 2-го рода содержат сложные оси, зеркальные плоскости, центр инверсии и описывают кристаллы, в которых есть зеркально равные части. Кристаллы, описываемые группами 1-го рода, могут кристаллизоваться в двух энантиоморфных формах («правой» и «левой», каждая из которых не содержит элементов симметрии 2-го рода), но зеркально равных друг другу.

В кристаллах элементы симметрии располагаются строго закономерным образом: их сочетания и взаимное расположение подчиняются математической теории абстрактных групп. Доказано, что взаимодействие двух операций симметрии порождает третью – результирующую – операцию (элемент симметрии). Рассмотрев все взаимодействия элементов симметрии кристалла, можно получить полную совокупность операций симметрии, называемую точечной группой симметрии кристалла (или кристаллографическим классом). Вывод точечных групп симметрии кристаллов впервые осуществил М. Л. Франкенгейм в 1826 г.; в 1867 г. А. В. Гадолин математически показал, что существует всего 32 точечные группы (класса) симметрии, полностью описывающие все возможные для кристаллов комбинации элементов симметрии. В зависимости от отношения масштабных отрезков их можно разделить на низшую, среднюю и высшую категории (рис. 2).

Рис. 2. Распределение 32 кристаллографических классов по категориям симметрии и сингониям. Иллюстрация: Николай Ерёмин.Рис. 2. Распределение 32 кристаллографических классов по категориям симметрии и сингониям. Иллюстрация: Николай Ерёмин.Внутри каждой категории симметрии существует деление на кристаллографические координатные системы, называемые сингониями, которые представляют собой объединения классов симметрии внутри категорий по принципу соотношения углов между координатными осями. Таким образом, классы симметрии, принадлежащие одной сингонии, «обслуживаются» одной и той же координатной системой.

В низшей категории выделяют три сингонии: триклинную, моноклинную и ромбическую. Самые низкосимметричные кристаллы характеризуются косоугольной координатной системой общего вида: $a \neq b \neq c$, $\alpha \neq \beta \neq \gamma \neq 90°$. Сингония с такой косоугольной координатной системой называется триклинной.

В кристаллах моноклинной сингонии один угол не равен 90° и его называют углом моноклинности, а ось, против которой он лежит, – осью моноклинности. Существует две равноправные установки, т. е. два варианта выбора осей моноклинного кристалла. В рациональной, или кристаллографической, установке $a \neq b \neq c$, $\alpha = \beta = 90°$, $\gamma \neq 90°$ ($\gamma$ – угол моноклинности, $z$– ось моноклинности), тогда как в минералогической установке, которая также преобладает в структурных исследованиях в химии, $a \neq b \neq c$, $\alpha = \gamma = 90°$, $\beta \neq 90°$ ($\beta$ – угол моноклинности, $y$– ось моноклинности).

Если же в системе координат кристалла присутствуют только прямые углы, то сингония называется ромбической: $a \neq b \neq c$, $\alpha = \beta = \gamma = 90°$.

В средней категории выделяют две сингонии: тетрагональную и гексагональную, координатные системы которых «обслуживают» кристаллы с осями 4-го, 3-го и 6-го порядков соответственно. Координатная система тетрагональной сингонии имеет следующие характеристики: $a = b \neq c$, $\alpha = \beta = \gamma = 90°$. А характеристики системы координат гексагональной сингонии таковы: $a = b \neq c$, $\alpha = \beta = 90$°, $\gamma = 120$. Обратим внимание, что такая координатная система «обслуживает» кристаллы, имеющие главную ось как 3-го, так и 6-го порядка. Поэтому внутри гексагональной сингонии выделяют две подсингонии: собственно гексагональную (если порядок главной оси равен 6) и тригональную (если порядок главной оси равен 3). Таким образом, достаточно часто встречающееся в литературе выделение отдельной тригональной сингонии с точки зрения современных рекомендаций Международного союза кристаллографов не совсем оправданно.

В высшей категории существует лишь одна сингония – кубическая с правой декартовой системой координат: $a = b = c$, $\alpha = \beta = \gamma = 90°$.

Пространственные группы симметрии

Описывают пространственную симметрию атомной структуры кристаллов. Трёхмерную периодичность кристаллов выражает пространственная решётка, которая задаёт трансляционную повторяемость эквивалентных точек кристаллического пространства в трёх некомпланарных направлениях. Параллелепипед повторяемости пространства, построенный на трёх кратчайших трансляционных векторах (трансляциях $\boldsymbol{T}$), совпадающих с направлениями максимальной симметрии (с направлением кристаллографических координатных осей), называется элементарной ячейкой кристалла. Вывод всех возможных в кристаллах элементарных ячеек осуществил О. Браве в 1855 г. Он показал, что существует всего 14 типов таких ячеек (решёток), описывающих внутреннюю периодическую симметрию кристаллов различных сингоний. Кроме примитивных $P$-ячеек, содержащих одну эквивалентную точку пространства (узел) на параллелепипед повторяемости, существуют базоцентрированные ячейки $С (B, A)$ (содержат два эквивалентных узла), объёмноцентрированные $I$ (два эквивалентных узла), дважды объёмноцентрированные $R$ (три эквивалентных узла) и гранецентрированные $F$-ячейки (четыре эквивалентных узла на параллелепипед повторяемости).

Трёхмерная периодичность структуры любого кристалла может быть отнесена к одной из этих 14 решёток. Подчеркнём, что даже в научной литературе часто смешивают термины «кристаллическая структура» и «кристаллическая решётка». Это является совершенно недопустимым, так как первое понятие относится к реальной картине атомного строения кристалла, а второе – к воображаемому геометрическому образу, описывающему трёхмерную периодичность в размещении атомов (или их групп) в кристаллическом пространстве. Различие между ними очевидно хотя бы потому, что огромному количеству разнообразных кристаллических структур соответствует всего лишь 14 решёток Браве.

Присутствие в бесконечных кристаллических структурах трансляций $\boldsymbol{T}$ не оставляет ни одну точку кристаллического пространства (в том числе и элементы макросимметрии) в единственном числе, а многократно повторяет их (транслирует) в определённых направлениях, создавая таким образом серии одинаковых элементов симметрии. Кроме того, трансляции взаимодействуют с элементами макросимметрии, в результате чего образуются специфические для трёхмерного бесконечного кристаллического пространства трансляционные (т. н. открытые) элементы симметрии: винтовые оси и плоскости скользящего отражения. Винтовые оси появляются в результате взаимодействия двух операций симметрии – поворота вокруг оси n-го порядка и одновременного переноса в направлении, параллельном оси, т. е. в результате взаимодействия поворота с трансляцией. В трёхмерном кристаллическом пространстве, кроме обычных поворотных осей 2-го, 3-го, 4-го и 6-го порядков, существуют винтовые оси 2₁, 3₁, 3₂, 4₁, 4₂, 4₃, 6₁, 6₂, 6₃, 6₄ и 6₅, реализующие поворот на определённый угол и одновременный перенос объекта на некоторую долю трансляционного вектора, указанную в подстрочном символе знака оси; например, ось 2₁ поворачивает на 180° и переносит на $(1/2)$$\boldsymbol{T}$, ось 3₂ поворачивает на 120° и переносит на $(2/3)$$\boldsymbol{T}$, ось 6₅ поворачивает на 60° и переносит на $(5/6)$$\boldsymbol{T}$ (рис. 3).

Рис. 3. Действие и графическое обозначение винтовых осей симметрии. Знаком «+» показаны высоты фигурок (+z) относительно нулевого уровня. Иллюстрация: Николай Ерёмин.Рис. 3. Действие и графическое обозначение винтовых осей симметрии. Знаком «+» показаны высоты фигурок (+z) относительно нулевого уровня. Иллюстрация: Николай Ерёмин.При взаимодействии трансляции $\boldsymbol{T}$ с плоскостями симметрии m возникают плоскости скользящего отражения $a, b, c, d, e, n$ и $g$ (обобщённый символ). Эти плоскости различаются направлением и величиной трансляционных сдвигов; например, координатные плоскости $a, b, c$ отражают и сдвигают на $(1/2)$$\boldsymbol{T}$ вдоль осей $x, y, z$ элементарной ячейки соответственно (рис. 4).

Рис. 4. Действие различных типов плоскостей скользящего отражения: а – плоскости а; б – плоскости с; в – плоскости n; г – плоскости d. Знаком «+» показаны высоты фигурок (+z) относительно нулевого уровня. Иллюстрация: Николай Ерёмин.Рис. 4. Действие различных типов плоскостей скользящего отражения: а – плоскости а; б – плоскости с; в – плоскости n; г – плоскости d. Знаком «+» показаны высоты фигурок (+z) относительно нулевого уровня. Иллюстрация: Николай Ерёмин.Таким образом, симметрия внутреннего строения кристаллов (кристаллических структур) описывается элементами симметрии макро- и микрокристаллографии (трансляциями, винтовыми осями и плоскостями скользящего отражения). Взаимодействие всех указанных элементов симметрии приводит к 230 возможным вариантам их сочетания – 230 законам упорядоченного расположения эквивалентных точек кристаллического вещества в трёхмерном периодическом пространстве (230 пространственным группам симметрии). Впервые они были выведены Е. С. Фёдоровым в 1890 г., поэтому в России их часто называют фёдоровскими группами. Любой кристалл относится к одной из этих групп симметрии; например, группа симметрии кристаллов меди – $\text{Fm} \bar{3} m$, магния – $\text{P}6_3/mmc$, алмаза – $\text{Fd} \bar{3} m$ и хлорида натрия – $\text{Fm} \bar{3}m$. По форме и симметрии элементарной ячейки все 230 пространственных групп также делятся на низшую, среднюю и высшую категории и шесть вышеуказанных сингоний.

Иногда при рассмотрении кристаллографического класса или пространственной группы симметрии вводят ещё одну переменную, имеющую какой-либо физический смысл (время, знак заряда, спин и т. п.). Если такая переменная имеет лишь два противоположных значения, то описание может быть проведено с использованием понятия антисимметрии (чёрно-белой симметрии); если же переменная имеет больше двух значений, то с помощью многоцветной симметрии. Такие группы симметрии в кристаллографии используют для описания кристаллических двойников, а также электрических, магнитных и других свойств кристаллов.