Чёрная дыра Райсснера – Нордстрёма
Чёрная дыра́ Ра́йсснера – Нордстрёма, геометрический объект (пространство-время), соответствующий решению уравнений Эйнштейна при наличии точечной массы с электрическим зарядом и при условиях статичности и сферической симметрии. Представляет собой сферически-симметричную (невращающуюся) электрически заряженную чёрную дыру. Масса и электрический заряд чёрной дыры Райсснера – Нордстрёма сконцентрированы в сингулярности пространства-времени, которая расположена в центре чёрной дыры и не может быть устранена никакими преобразованиями координат, поскольку инварианты тензора кривизны в ней являются бесконечными. Это решение уравнений Эйнштейна было получено в 1916–1921 гг. независимо Г. Райсснером, Г. Вейлем, Г. Нордстрёмом и Дж. Джеффери.
Метрика Райсснера – Нордстрёма
Все свойства чёрной дыры Райсснера – Нордстрёма определяются метрикой соответствующего сферически-симметричного пространства-времени (называемой метрикой Райсснера – Нордстрёма), в котором квадрат четырёхмерного интервала между двумя бесконечно близкими событиями равен
Здесь – соответственно радиальная и две угловые координаты в сферической системе координат с центром в сингулярности; – временная координата; – гравитационная постоянная, – скорость света в вакууме; – гравитационный радиус, – параметр массы (если чёрная дыра образовалась в результате гравитационного коллапса физического объекта, то параметр массы равен массе этого объекта); – параметр заряда, имеющий размерность длины, – электрический заряд, – постоянная, входящая в закон Кулона. При решение Райсcнера – Нордстрёма переходит в решение Шварцшильда.
Световые конусы пространства-времени Райсснера – Нордстрёма и горизонты событий
На рис. 1 изображены световые конусы для пространства-времени, описываемого решением Райсснера – Нордстрёма. Предполагается движение по радиальным направлениям, поэтому используются только координаты и Это координаты удалённого наблюдателя в его собственной системе отсчёта. Угол при вершине световых конусов определяется выражением для скорости света (фотонов), которая измеряется удалённым наблюдателем:
Это выражение следует из формулы (1) и уравнения для безмассовых частиц. Скорости массивных частиц всегда меньше световых, поэтому их мировые линии расположены внутри этих конусов. Толстые вертикальные линии, обозначенные как и также удовлетворяют уравнению и дополнительно соответствуют условию Они обозначают сферические поверхности и которые называются горизонтами событий (соответственно, внутренним и внешним). Их координаты равны
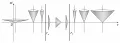 Рис. 1. Световые конусы для пространства-времени чёрной дыры Райсснера – Нордстрёма. Предполагается движение по радиальному направлению, поэтому используются только радиальная пространственная координата r и временна́я координата t. Сингулярность находится в начале координат. Архив БРЭ.На значительном удалении от центральной точки (правая часть рис. 1, при ) образующие конусов наклонены к осям координат под углом 45°, т. е. так, как в плоском пространстве-времени (пространстве-времени с нулевой кривизной, или в пространстве-времени Минковского). По мере приближения к внешнему горизонту световые конусы становятся у́же, а на поверхности полностью «сжимаются», превращаясь в вертикальную линию. Это значит, что в собственной системе отсчёта удалённого наблюдателя скорость света на поверхности становится «нулевой» (это также видно из вышеназванного условия ) и, следовательно, никакие частицы, включая фотоны, не могут достигнуть этой поверхности или покинуть её. С точки зрения удалённого наблюдателя все процессы на горизонте событий чёрной дыры «замораживаются». Траектории электрически нейтральных и заряженных частиц будут различными, но световые конусы их ограничивают одинаково.
Рис. 1. Световые конусы для пространства-времени чёрной дыры Райсснера – Нордстрёма. Предполагается движение по радиальному направлению, поэтому используются только радиальная пространственная координата r и временна́я координата t. Сингулярность находится в начале координат. Архив БРЭ.На значительном удалении от центральной точки (правая часть рис. 1, при ) образующие конусов наклонены к осям координат под углом 45°, т. е. так, как в плоском пространстве-времени (пространстве-времени с нулевой кривизной, или в пространстве-времени Минковского). По мере приближения к внешнему горизонту световые конусы становятся у́же, а на поверхности полностью «сжимаются», превращаясь в вертикальную линию. Это значит, что в собственной системе отсчёта удалённого наблюдателя скорость света на поверхности становится «нулевой» (это также видно из вышеназванного условия ) и, следовательно, никакие частицы, включая фотоны, не могут достигнуть этой поверхности или покинуть её. С точки зрения удалённого наблюдателя все процессы на горизонте событий чёрной дыры «замораживаются». Траектории электрически нейтральных и заряженных частиц будут различными, но световые конусы их ограничивают одинаково.
Если рассматривать падение частицы в чёрную дыру не в системе отсчёта удалённого наблюдателя, а в её собственной системе отсчёта, то она может достигнуть горизонта событий и даже пересечь его, но после этого также не сможет вернуться обратно. Это свидетельствует о том, что гравитационное притяжение в окрестностях горизонтов событий является экстремально сильным.
Лучи света, проходящие вблизи чёрной дыры, отклоняются от прямой линии. Чем ближе к горизонту событий проходит луч, тем больше угол отклонения. Как и в случае с чёрной дырой Шварцшильда, на определённом расстоянии от горизонта событий луч света может развернуться на 180° и уйти в обратном направлении. При ещё меньшем расстоянии угол отклонения станет равным 360° и больше. Может оказаться, что луч сделает полный оборот и останется на круговой (замкнутой) орбите вокруг чёрной дыры. Эта траектория луча называется фотонной орбитой, она неустойчива: после любого возмущения луч либо покинет чёрную дыру, либо «упадёт» в неё.
На горизонтах событий и коэффициент при в формуле для интервала (1) обращается в ноль, а коэффициент при становится бесконечным. Тем не менее это не означает наличие на этой сфере геометрической особенности (сингулярности) пространства-времени, поскольку инварианты тензора кривизны на этих поверхностях в бесконечность не обращаются. Расходимость компонент метрического тензора на горизонтах в данном случае – это следствие выбора конкретной системы координат . Другими словами, это координатная, а не истинная сингулярность. По этой причине невозможно описать достижение пробными частицами горизонта в координатах
Между и коэффициент при становится отрицательным, а коэффициент при – положительным, т. е. координата становится пространственной, а координата становится временно́й. По этой причине световые конусы развернутся на 90° (рис. 1). Из расположения световых конусов становится очевидным, что массивные частицы, распространяясь от внешнего горизонта , неминуемо достигнут внутреннего горизонта а фотоны будут стремиться к только асимптотически – это также координатный эффект. При исходный смысл координат и восстанавливается. По этой причине истинная сингулярность при в чёрной дыре Райсснера – Нордстрёма на самом деле представляет собой точку (в отличие от чёрной дыры Шварцшильда, где – это пространственноподобная гиперповерхность). Положение световых конусов при говорит о том, что в этой области отсутствует неизбежность падения в сингулярность.
Соотношение между положением горизонтов и следующее. Как видно из формул (2) и (3), в случае чёрная дыра Райсснера – Нордстрёма переходит в чёрную дыру Шварцшильда с единственным горизонтом: При добавлении малого электрического заряда появляется внутренний горизонт с малой величиной (меньшей, чем ), а величина становится меньше По мере роста величина увеличивается, а величина уменьшается. При два горизонта событий и совпадут, образуя единый горизонт. Дальнейшее увеличение приводит к выполнению условия и исчезновению горизонтов событий, а значит, и отсутствию чёрной дыры; истинная сингулярность становится «голой» сингулярностью. Теоретически такая ситуация возможна, однако существует принцип космической цензуры (пока не доказанный), согласно которому в нашей Вселенной не должно существовать «голых» сингулярностей.
Замедление времени и гравитационное красное смещение
Пусть вдоль радиальной координаты снаружи сферы расположено множество неподвижных наблюдателей. Все наблюдатели оснащены одинаковыми собственными часами, которые для каждого из них идут одинаково (но в сравнении друг с другом их время может течь по-разному). Для наблюдателя на бесконечности (при бесконечном ) его собственное время (показание его собственных часов) совпадает с координатным временем Наблюдаемые им показания часов наблюдателей, более близких к горизонту событий чёрной дыры, определяются выражением
которое вытекает из временно́й части формулы (1) для интервала. Из выражения (4) следует, что при чем меньше тем меньше т. е. для удалённого наблюдателя чем часы ближе к внешнему горизонту событий чёрной дыры, тем они идут медленнее. При часы должны застыть при любом Это относится не только к часам, но и ко всем наблюдаемым процессам.
С эффектом замедления времени связан эффект гравитационного красного смещения. Пусть первый наблюдатель (излучатель), находящийся вблизи внешнего горизонта событий (но снаружи него), посылает второму (удалённому) наблюдателю световой сигнал, который в системе отсчёта излучателя имеет частоту Для удалённого наблюдателя часы излучателя идут медленнее его собственных, поэтому и световой сигнал он будет принимать с меньшей частотой т. е. происходит смещение частоты в длинноволновую (красную) область спектра. Чем ближе к сфере радиуса находится источник сигнала, тем больше красное смещение. Если удалённый наблюдатель попытается зафиксировать сигнал, испущенный со сферы радиуса он обнаружит, что сигнала нет, т. е. его частота нулевая.
Диаграмма Пенроуза и переход в другую вселенную
Помимо того, что координаты в формуле (1) и на рис. 1 являются сингулярными на горизонтах событий, они не покрывают всей геометрии пространства-времени Райсснера – Нордстрёма. Для описания полной геометрии чёрных дыр используются, например, конформные координаты и соответствующие им конформные диаграммы Пенроуза. На рис. 2 представлена такая диаграмма для геометрии Райсснера – Нордстрёма, где полное пространство-время представлено бесконечным набором идентичных «фрагментов».
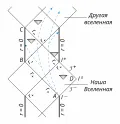 Рис. 2. Конформная диаграмма Пенроуза для геометрии Райсснера – Нордстрёма.
Архив БРЭ.Четырёхугольник ABCD соответствует диаграмме на рис. 1. «Наша Вселенная» в данном случае определяется как область пространства-времени, находящаяся снаружи внешнего горизонта событий в которой находится удалённый наблюдатель. Для нашей Вселенной временны́е бесконечности прошлого и будущего представлены точками и пространственная бесконечность – точкой нулевые бесконечности, откуда приходят и куда уходят световые сигналы, – отрезками и В отличие от рис. 1, на рис. 2 образующие световых конусов в каждой из точек, включая горизонты и имеют один и тот же наклон в 45°. Штриховыми голубыми линиями обозначены мировые линии массивных частиц. Как видно из диаграммы, попадая под горизонт любой сигнал неминуемо достигнет следующего горизонта В отличие от чёрной дыры Шварцшильда, частица (сигнал) вполне может избежать столкновения с истинной сингулярностью, благодаря возможности выйти в другую вселенную. Для других вселенных пространственные, временны́е и нулевые бесконечности определяются так же, как и для нашей.
Рис. 2. Конформная диаграмма Пенроуза для геометрии Райсснера – Нордстрёма.
Архив БРЭ.Четырёхугольник ABCD соответствует диаграмме на рис. 1. «Наша Вселенная» в данном случае определяется как область пространства-времени, находящаяся снаружи внешнего горизонта событий в которой находится удалённый наблюдатель. Для нашей Вселенной временны́е бесконечности прошлого и будущего представлены точками и пространственная бесконечность – точкой нулевые бесконечности, откуда приходят и куда уходят световые сигналы, – отрезками и В отличие от рис. 1, на рис. 2 образующие световых конусов в каждой из точек, включая горизонты и имеют один и тот же наклон в 45°. Штриховыми голубыми линиями обозначены мировые линии массивных частиц. Как видно из диаграммы, попадая под горизонт любой сигнал неминуемо достигнет следующего горизонта В отличие от чёрной дыры Шварцшильда, частица (сигнал) вполне может избежать столкновения с истинной сингулярностью, благодаря возможности выйти в другую вселенную. Для других вселенных пространственные, временны́е и нулевые бесконечности определяются так же, как и для нашей.
В случае горизонты и «сливаются». Однако, в отличие от чёрной дыры Шварцшильда, координаты и не меняют смысла под «сдвоенным» горизонтом. Поэтому диаграмма Пенроуза оказывается «половиной» диаграммы на рис. 2, где вертикальная линия, проведённая по центру рисунка и представляющая истинную сингулярность, оставит либо правую, либо левую часть. В этом случае также есть возможность избежать попадания в истинную сингулярность путём выхода в другую вселенную. Наконец, в случае «голой» сингулярности диаграмма Пенроуза вырождается в единственный треугольник, где слева вертикалью будет обозначена сингулярность, а справа – вся остальная Вселенная.
Заряженная чёрная дыра может сформироваться в результате гравитационного коллапса только в случае, если величина заряда чрезвычайно мала по отношению к массе. Ведь гравитационное притяжение материи должно компенсировать её электрическое отталкивание, которое значительно сильнее. «Голая» заряженная сингулярность заведомо не может образоваться путём коллапса.
