Чёрная дыра Шварцшильда
Чёрная дыра́ Шва́рцшильда, геометрический объект (пространство-время), соответствующий решению уравнений Эйнштейна в вакууме при наличии точечной массы и при условиях статичности и сферической симметрии метрики пространства-времени. Представляет собой сферически-симметричную (не вращающуюся) чёрную дыру, не обладающую электрическим зарядом. В центре чёрной дыры Шварцшильда расположена сингулярность пространства-времени, в которой сконцентрирована вся её масса. Она окружена горизонтом событий, из-под которого невозможно распространение никаких сигналов.
Метрика Шварцшильда
В 1916 г. К. Шварцшильд нашёл общее решение уравнений Эйнштейна в вакууме, которое описывает пространство-время вокруг любого массивного изолированного сферически-симметричного (невращающегося) и электрически не заряженного тела. Если масса сконцентрирована в одной точке – сингулярности пространства-времени, то соответствующий объект является чёрной дырой и называется чёрной дырой Шварцшильда. Все свойства чёрной дыры Шварцшильда определяются метрикой соответствующего сферически-симметричного пространства-времени (называемой метрикой Шварцшильда), в котором квадрат четырёхмерного интервала между двумя бесконечно близкими событиями равен
Здесь – соответственно радиальная и две угловые координаты в сферической системе координат с центром в сингулярности; – временна́я координата; – гравитационная постоянная, – скорость света в вакууме; – гравитационный радиус, – параметр массы (если чёрная дыра образовалась в результате гравитационного коллапса физического объекта, то параметр массы равен массе этого объекта). Гравитационный радиус фактически является константой интегрирования, выбранной таким образом, чтобы на достаточно больших расстояниях от центра чёрной дыры движение материальных объектов в пространстве-времени, описываемом метрикой Шварцшильда в координатах подчинялось закону всемирного тяготения Ньютона. При метрика Шварцшильда стремится к метрике плоского пространства-времени (т. е. пространства-времени с нулевой кривизной, или пространства-времени Минковского) в сферических координатах. При метрика Шварцшильда также переходит в метрику плоского пространства-времени.
Световые конусы пространства-времени Шварцшильда и горизонт событий
На рис. 1 изображены световые конусы для пространства-времени, описываемого решением Шварцшильда. Предполагается движение по радиальным направлениям, поэтому используются только координаты и Это координаты удалённого наблюдателя в его собственной системе отсчёта. Угол при вершине световых конусов определяется выражением для скорости света (фотонов), которая измеряется удалённым наблюдателем:
Это выражение следует из формулы (1) и уравнения для безмассовых частиц. Скорости массивных частиц всегда меньше скорости света, поэтому их мировые линии расположены внутри этих конусов. Вертикальные линии соответствуют неподвижным телам.
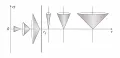 Рис. 1. Световые конусы для пространства-времени чёрной дыры Шварцшильда. Предполагается движение по радиальному направлению, поэтому используются только радиальная пространственная координата r и временная координата t.На значительном удалении от центральной точки (сингулярности) образующие конусов наклонены к осям координат под углом 45°, т. е. так, как в плоском пространстве-времени. По мере приближения к центру конусы становятся у́же, при они «сжимаются» и превращаются в вертикальную линию. Таким образом, для удалённого наблюдателя скорость света становится «нулевой», а это означает, что как свет, так и массивные частицы никогда не достигнут сферы гравитационного радиуса и при приближении к ней все процессы «замораживаются». Этот же эффект «сжатия» световых конусов при говорит о том, что никакие сигналы, в том числе фотоны, не могут покинуть сферу гравитационного радиуса – настолько сильным оказывается гравитационное притяжение на ней.
Рис. 1. Световые конусы для пространства-времени чёрной дыры Шварцшильда. Предполагается движение по радиальному направлению, поэтому используются только радиальная пространственная координата r и временная координата t.На значительном удалении от центральной точки (сингулярности) образующие конусов наклонены к осям координат под углом 45°, т. е. так, как в плоском пространстве-времени. По мере приближения к центру конусы становятся у́же, при они «сжимаются» и превращаются в вертикальную линию. Таким образом, для удалённого наблюдателя скорость света становится «нулевой», а это означает, что как свет, так и массивные частицы никогда не достигнут сферы гравитационного радиуса и при приближении к ней все процессы «замораживаются». Этот же эффект «сжатия» световых конусов при говорит о том, что никакие сигналы, в том числе фотоны, не могут покинуть сферу гравитационного радиуса – настолько сильным оказывается гравитационное притяжение на ней.
Несмотря на то что существует понятие единого пространства-времени, физические сущности пространства и времени различны. Это выражается в том, что временна́я и пространственная части входят в выражение для интервала (1) с разными знаками: первая – со знаком «плюс», вторая – со знаком «минус». Это соответствует решению Шварцшильда вне сферы Внутри этой сферы ситуация меняется. При коэффициент при становится отрицательным, а коэффициент при – положительным, т. е. координата становится пространственной, а координата становится временно́й. Учитывая этот факт, световые конусы при развернутся на 90° (рис. 1). С внутренней стороны сферы их угол при вершине равен 180°, по мере приближения к центру этот угол уменьшается, а при становится равным 0°, т. е. конусы снова «сжимаются». Поскольку мировая линия частицы с ненулевой массой всегда находится внутри светового конуса, то такая частица, оказавшись на или под поверхностью неминуемо достигнет центральной «точки» при . Фотоны, испущенные с поверхности радиусом в направлении от центра, останутся на этой поверхности. Мировые линии остальных фотонов заканчиваются в «точке» Это означает, что никакие сигналы не могут покинуть поверхность и область под ней. По этим причинам поверхность называется горизонтом событий, а сам объект – чёрной дырой. Эти выводы справедливы в рамках общей теории относительности, которая является классической (не квантовой) теорией. Учёт квантовых эффектов может их изменить.
Если чёрная дыра достаточно массивная (следовательно, большая), то локально её горизонт событий довольно плоский и падающий в чёрную дыру наблюдатель никак не заметит его пересечения. Однако по мере дальнейшего падения наблюдатель начнёт ощущать действие приливных сил: его начнёт «растягивать» в направлении радиуса и «сжимать» в перпендикулярных направлениях. Чем меньше размер чёрной дыры, тем больше создаваемые ею приливные силы на горизонте событий.
Искривление лучей света и фотонная сфера
Вблизи горизонта событий проявления сильного гравитационного притяжения чрезвычайно выражены. Распространение лучей света вблизи чёрной дыры Шварцшильда показано на рис. 2. Как и в окрестности любого объекта, обладающего гравитационным полем, эти лучи отклоняются от прямой линии. 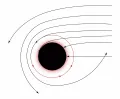 Рис. 2. Траектории лучей света вблизи чёрной дыры Шварцшильда. Красным цветом выделена фотонная орбита.При достаточном приближении к сфере радиусом луч может обогнуть объект и уйти в обратном направлении. На расстоянии от центра угол отклонения станет равным 360°, т. е. луч сделает полный оборот. Эта траектория луча называется фотонной орбитой, она неустойчива: после любого возмущения луч либо покинет чёрную дыру, либо «упадёт» в неё. Сфера радиусом на которой лежит фотонная орбита, называется фотонной сферой. Если продолжить приближение луча к центру, то его траектория превратится в спираль и он будет захвачен чёрной дырой.
Рис. 2. Траектории лучей света вблизи чёрной дыры Шварцшильда. Красным цветом выделена фотонная орбита.При достаточном приближении к сфере радиусом луч может обогнуть объект и уйти в обратном направлении. На расстоянии от центра угол отклонения станет равным 360°, т. е. луч сделает полный оборот. Эта траектория луча называется фотонной орбитой, она неустойчива: после любого возмущения луч либо покинет чёрную дыру, либо «упадёт» в неё. Сфера радиусом на которой лежит фотонная орбита, называется фотонной сферой. Если продолжить приближение луча к центру, то его траектория превратится в спираль и он будет захвачен чёрной дырой.
Вследствие этих эффектов наблюдатель, приближающийся к чёрной дыре Шварцшильда, будет видеть следующую картину. Издалека объект воспринимается как чёрное пятно, вокруг которого наблюдается обычное распределение звёзд. По мере приближения к объекту чёрное пятно увеличивается. На расстояниях, близких к фотонной орбите, наблюдатель будет встречать лучи света, которые обогнули чёрную дыру и развернулись в обратном направлении, вследствие чего вокруг чёрного пятна вместе с прежними звёздами он увидит и звёзды, находящиеся позади него. Внутри фотонной орбиты позади себя он увидит обычные звёзды и те, которые реально перед ним. Траектории массивных частиц, пролетающих мимо чёрной дыры на расстояниях, сравнимых с ведут себя похожим образом.
Замедление времени и гравитационное красное смещение
Пусть вдоль радиальной координаты снаружи сферы расположено множество неподвижных наблюдателей (зафиксированных, например, с помощью ракетных двигателей). Все наблюдатели оснащены одинаковыми собственными часами, которые для каждого из них идут одинаково (но в сравнении друг с другом их время может течь по-разному). Для наблюдателя на бесконечности (при бесконечном ) его собственное время (показание его собственных часов) совпадает с координатным временем Наблюдаемые им показания часов наблюдателей, более близких к центру чёрной дыры, определяются выражением
которое следует из временно́й части формулы (1) для интервала. Отсюда видно, что чем меньше тем меньше т. е. для удалённого наблюдателя чем часы ближе к горизонту событий чёрной дыры, тем они идут медленнее. При часы должны «застыть» при любом Это относится не только к часам, а ко всем наблюдаемым процессам.
С эффектом замедления времени связан эффект гравитационного красного смещения. Пусть первый наблюдатель (излучатель), находящийся вблизи горизонта событий (но снаружи него), посылает второму (удалённому) наблюдателю световой сигнал, который в системе отсчёта излучателя имеет частоту Для удалённого наблюдателя часы излучателя идут медленнее его собственных, поэтому и световой сигнал он будет принимать с меньшей частотой т. е. происходит смещение частоты в длинноволновую (красную) область спектра. Чем ближе к сфере радиуса находится источник сигнала, тем больше красное смещение. Если удалённый наблюдатель попытается зафиксировать сигнал, испущенный со сферы радиуса он обнаружит, что сигнала нет, т. е. его частота нулевая.
Координатная и истинная сингулярности
Из формулы для метрики Шварцшильда (1) следует, что на сфере коэффициент при обращается в ноль, а коэффициент при становится бесконечным. Тем не менее это не означает наличие на этой сфере геометрической особенности (сингулярности) пространства-времени, поскольку критерием такой особенности являются инварианты тензора кривизны пространства-времени, которые при не обращаются в бесконечность. Расходимость компонент метрического тензора в данном случае – это следствие выбора конкретной системы координат для описания окрестности (т. н. сингулярной системы координат). Именно по этой причине невозможно описать достижение пробными частицами сферы радиуса в координатах и проникновение под неё. Существует множество систем координат, включая собственные координаты свободно падающих наблюдателей, где этой проблемы нет. В таких координатах мировые линии пробных частиц непрерывным образом достигают сферы и уходят под неё.
Метрика пространства-времени (1) при также имеет особенности: коэффициент при обращается в отрицательную бесконечность, а коэффициент при становится нулевым, но на этот раз особенность не координатная. Поскольку инварианты тензора кривизны обращаются в бесконечность, то для имеет место сингулярность пространства-времени, или истинная сингулярность (геометрическая сингулярность) чёрной дыры.
При падении вещества в центр чёрной дыры и, как следствие, его сильном сжатии плотность и давление достигнут таких высоких значений, при которых известные законы физики не работают. Скорее всего, пространство, время и материя перестанут описываться теориями классической (не квантовой) физики и вывод общей теории относительности о неизбежном падении всей материи в точку может быть неверен.
Диаграмма Пенроуза и белая дыра
Кроме того, что координаты в выражении (1) и на рис. 1 являются сингулярными на горизонте событий, они не покрывают всей геометрии Шварцшильда. Для описания полной геометрии чёрных дыр используются, например, конформные координаты и соответствующие им конформные диаграммы Пенроуза. На рис. 3 представлена такая диаграмма для геометрии Шварцшильда. Из диаграммы следует, что координаты и формула (1) могут описать только половину геометрии Шварцшильда. Диаграмма на рис. 1 соответствует только половине диаграммы на рис. 3, которая расположена выше прямой AB и представляет чёрную дыру. Диаграмма ниже AB представляет белую дыру. (Аналогичная интерпретация имеет место относительно второй диагонали, ортогональной АВ и также делящей диаграмму на рис. 3 на равные части.)
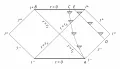 Рис. 3. Конформная диаграмма Пенроуза для геометрии Шварцшильда.Использование конформных координат позволяет представить пространство-время в компактной форме (рис. 3). Временны́е бесконечности прошлого и будущего представлены точками и соответственно; пространственные бесконечности – точками нулевые бесконечности, из которых приходят и на которые уходят световые сигналы, – отрезками и Горизонты событий обозначены отрезками истинные сингулярности – отрезками Образующие световых конусов в каждой точке диаграммы на рис. 3 имеют наклон 45°. По этой причине легко прослеживается история любой массивной частицы или фотона, падающих в дыру и не встречающих препятствий на горизонте событий (линии AC и DE на рис. 3 соответственно). Сингулярности на диаграмме представлены в виде горизонтальных (пространственноподобных) отрезков (а не точек), потому что под горизонтом событий координаты поменяли смысл, вследствие чего представляет собой пространственноподобную сингулярную гиперповерхность.
Рис. 3. Конформная диаграмма Пенроуза для геометрии Шварцшильда.Использование конформных координат позволяет представить пространство-время в компактной форме (рис. 3). Временны́е бесконечности прошлого и будущего представлены точками и соответственно; пространственные бесконечности – точками нулевые бесконечности, из которых приходят и на которые уходят световые сигналы, – отрезками и Горизонты событий обозначены отрезками истинные сингулярности – отрезками Образующие световых конусов в каждой точке диаграммы на рис. 3 имеют наклон 45°. По этой причине легко прослеживается история любой массивной частицы или фотона, падающих в дыру и не встречающих препятствий на горизонте событий (линии AC и DE на рис. 3 соответственно). Сингулярности на диаграмме представлены в виде горизонтальных (пространственноподобных) отрезков (а не точек), потому что под горизонтом событий координаты поменяли смысл, вследствие чего представляет собой пространственноподобную сингулярную гиперповерхность.
