Чёрная дыра Керра
Чёрная дыра́ Ке́рра (вращающаяся чёрная дыра), геометрический объект (пространство-время), соответствующий решению уравнений Эйнштейна в вакууме при наличии массы и момента импульса которые сконцентрированы в сингулярности пространства-времени. Сингулярность расположена в центральной области чёрной дыры и имеет форму кольца (центр чёрной дыры в системе координат удалённого наблюдателя соответствует диску в экваториальной плоскости чёрной дыры, а сингулярность – граница этого диска).
В зависимости от соотношения параметров и сингулярность может быть окружена либо двумя горизонтами событий (внутренним и внешним), либо одним. Кроме того, возможно такое соотношение массы и момента импульса, при котором горизонтов событий нет, т. е. решение представляет собой «голую» сингулярность, а не чёрную дыру. При наличии хотя бы одного горизонта событий удалённый наблюдатель регистрирует многие из эффектов в окрестности внешнего горизонта, аналогичные эффектам для чёрной дыры Шварцшильда и других чёрных дыр.
Данное решение было получено в 1963 г. Р. Керром (Kerr, 1963) и является чрезвычайно важным, поскольку подавляющее число астрофизических объектов вращается. Если возможен их гравитационный коллапс, то он должен привести к возникновению чёрных дыр, гравитационное поле которых описывается решением Керра.
Метрика Керра и горизонты событий
Все свойства чёрной дыры Керра определяются метрикой соответствующего пространства-времени (называемой метрикой Керра), которая является точным решением уравнений Эйнштейна. В этом пространстве-времени квадрат четырёхмерного интервала между двумя бесконечно близкими событиями в упрощённом виде имеет следующий вид (точную запись см. в: Хокинг. 1977. С. 180):
Здесь – соответственно радиальная и две угловые пространственные координаты; – временна́я координата (собственное время удалённого на бесконечность наблюдателя); – скорость света в вакууме; – компоненты метрического тензора (метрические коэффициенты), которые помимо пространственных координат и зависят также от массы и момента импульса Координаты выбираются таким образом, чтобы описание гравитационного поля чёрной дыры на достаточно большом удалении от неё соответствовало закону всемирного тяготения Ньютона, записанному в сферической системе координат. Перекрёстный член в силу наличия вращения (момента импульса ) не может быть исключён никаким преобразованием координат. Метрика Керра также позволяет определить радиальные координаты внутреннего и внешнего горизонтов событий – соответственно и
Для оценки соотношений между массой и моментом импульса чёрной дыры Керра используются величины с размерностью длины: гравитационный радиус (где – гравитационная постоянная) и параметр момента импульса
В случае чёрная дыра Керра становится чёрной дырой Шварцшильда с единственным (внешним) горизонтом событий:
При возникновении момента импульса появляется внутренний горизонт событий с радиальной координатой
окружающий сингулярность, а внешний горизонт событий становится меньше его радиальная координата определяется выражением
С ростом но при внутренний горизонт событий увеличивается, а внешний уменьшается. При два горизонта сливаются в один, с координатой
При горизонты событий исчезают и чёрная дыра превращается в «голую» сингулярность. Однако существует принцип космической цензуры (пока не доказанный), согласно которому в нашей Вселенной не должно существовать «голых» сингулярностей.
Любая поверхность включая горизонты событий, в пространстве-времени, описываемом метрикой Керра, является софокусным эллипсоидом (сфероидом), а не сферой. При сфероиды вырождаются в диск радиусом граница которого и является кольцевой сингулярностью пространства-времени.
Замедление времени на горизонте событий и свободное падение в чёрную дыру
Пусть вдоль радиальной координаты снаружи внешнего горизонта событий расположено множество неподвижных наблюдателей. Все наблюдатели оснащены одинаковыми собственными часами, которые для каждого из них идут одинаково (но в сравнении друг с другом их время может течь по-разному). Для наблюдателя на бесконечности (при бесконечном ) его собственное время (показание его собственных часов) совпадает с координатным временем Регистрируемые им показания часов других наблюдателей, более близких к горизонту событий будут меньше его собственных показаний: причём чем ближе к горизонту событий часы, тем меньше их показания Другими словами, для удалённого наблюдателя чем часы ближе к внешнему горизонту событий чёрной дыры, тем медленнее они идут. Это относится не только к часам, а ко всем наблюдаемым процессам. Все процессы, происходящие на горизонте событий, для удалённого наблюдателя должны «застыть».
Из этого эффекта следует, что с точки зрения удалённого наблюдателя другой наблюдатель, свободно падающий в чёрную дыру, никогда не достигнет горизонта событий. Однако в собственной системе отсчёта свободно падающего наблюдателя он сможет достигнуть внешнего горизонта событий и беспрепятственно пересечь его. После этого покинуть чёрную дыру для него станет невозможно, поскольку гравитационное притяжение в окрестностях горизонта событий становится чрезвычайно сильным.
Лучи света, проходящие вблизи чёрной дыры, отклоняются от прямой линии; чем ближе к горизонту событий проходит луч, тем больше угол отклонения. Как и в случае с чёрной дырой Шварцшильда, на определённом расстоянии от горизонта событий луч света может развернуться и уйти в обратном направлении. При дальнейшем уменьшении расстояния луч света может обогнуть чёрную дыру (возможно, многократно) и уйти либо на бесконечность, либо под горизонт событий. Если луч распространяется в экваториальной плоскости чёрной дыры, то для него существуют две замкнутые круговые орбиты (в зависимости от направления распространения света по отношению к вращению дыры) с радиусами
где знак «минус» соответствует распространению света по направлению вращения дыры, знак «плюс» – против её вращения. Эти траектории луча называются фотонными орбитами, они неустойчивы: после любого возмущения луч либо покинет чёрную дыру, либо «упадёт» в неё.
С эффектом замедления времени также связан эффект гравитационного красного смещения. Пусть первый наблюдатель (излучатель) вблизи посылает второму (удалённому) наблюдателю световой сигнал, который в системе отсчёта излучателя имеет частоту . Для удалённого наблюдателя часы излучателя идут медленнее его собственных, поэтому и световой сигнал он будет принимать с меньшей частотой т. е. происходит смещение частоты в длинноволновую (красную) область спектра. Чем ближе к сфере радиуса находится источник сигнала, тем больше красное смещение. Если удалённый наблюдатель попытается зафиксировать сигнал, испущенный со сферы радиуса он обнаружит, что сигнала нет, т. е. его частота нулевая.
Попадая под внешний горизонт событий, наблюдатель неминуемо достигнет внутреннего горизонта событий Однако под внутренним горизонтом он имеет возможность либо достичь кольцевой сингулярности, либо избежать попадания в сингулярность благодаря переходу в другие вселенные. Причём, попадая в другие вселенные, наблюдатель всё ещё имеет альтернативу попасть в ту или иную сингулярность или избежать их. При слиянии горизонтов эти свойства не изменяются. Наблюдатель будет поглощён истинной сингулярностью только в том случае, если он будет падать в центр в экваториальной плоскости чёрной дыры. В других случаях он либо пройдёт мимо сингулярности снаружи неё, уходя в другую вселенную, либо попадёт внутрь кольца. В последнем случае за плоскостью кольца пространство становится «отрицательным» (т. е. ). Это соответствует решению уравнений Эйнштейна с отрицательной массой, от которой пробная частица с положительной массой отталкивается, т. е. с проявлением «антигравитации». Ещё одно необычное свойство пространства-времени «за кольцом» – это нарушение причинности вблизи кольца. Свойства кольцевой сингулярности не меняются, если она становится «голой». Согласно некоторым моделям, кольцевая сингулярность с такими свойствами может представлять собой кротовую нору.
Эргосфера
Вокруг чёрной дыры Керра существует т. н. граница стационарности для вращательного движения, описываемая уравнением
которая представляет собой осесимметричную замкнутую поверхность с топологией сферы, «сжатую» с полюсов. Она окружает внешний горизонт событий, касаясь его полюсами. Пространство между границей стационарности и внешним горизонтом событий называется эргосферой. Это область, где любой наблюдатель не может оставаться в состоянии покоя и, «увлекаемый» вращением чёрной дыры, вынужден совершать круговое движение вокруг неё, не имея возможности противостоять этому. Однако, не достигая горизонта событий, такой наблюдатель имеет возможность избежать падения в чёрную дыру и покинуть её.
В 1969 г. Р. Пенроуз предложил механизм извлечения энергии из вращающейся чёрной дыры (Penrose, 1969). Во время такого процесса падающее в чёрную дыру тело делится в эргосфере на две части, одна из которых достигает горизонта и уходит под него, а вторая может вернуться обратно с полной энергией, большей, чем полная энергия исходного (целого) тела. В результате вращение чёрной дыры замедляется.
Диаграмма Пенроуза и переход в другие вселенные
Сложный характер решения Керра приводит к необходимости использования разных систем координат для описания различных эффектов, связанных с особенностями геометрии данного пространства-времени. Наиболее универсальными являются конформные координаты и соответствующие им диаграммы Пенроуза (рисунок), которые качественно близки к диаграммам Пенроуза для чёрной дыры Райсснера – Нордстрёма. Использованные выше координаты способны описать только часть геометрии Керра, представленную на диаграмме четырёхугольником ABCD. Конформные же координаты дают возможность описать полную геометрию Керра, представленную бесконечным набором идентичных «фрагментов» пространства-времени. «Наша Вселенная» в данном случае определяется как область пространства-времени, находящаяся снаружи внешнего горизонта событий в которой находится удалённый наблюдатель. Для нашей Вселенной временны́е бесконечности прошлого и будущего на диаграмме представлены точками и пространственная бесконечность – точкой нулевые бесконечности, откуда приходят и куда уходят световые сигналы, – отрезками и
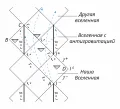 Конформная диаграмма Пенроуза для геометрии Керра.
Архив БРЭ.Как и для чёрных дыр Шварцшильда и Райсснера – Нордстрёма, распространение любых сигналов в каждой из точек диаграммы, включая горизонты и ограничено образующими световых конусов, которые везде имеют один и тот же наклон в 45°. Как видно из диаграммы, попадая под горизонт сигнал неминуемо достигнет следующего горизонта В отличие от чёрной дыры Шварцшильда, частица (сигнал) может избежать столкновения с сингулярностью, благодаря возможности выйти в другую вселенную. Кроме этого, есть возможность через сингулярное кольцо проникнуть во вселенную с «антигравитацией».
Конформная диаграмма Пенроуза для геометрии Керра.
Архив БРЭ.Как и для чёрных дыр Шварцшильда и Райсснера – Нордстрёма, распространение любых сигналов в каждой из точек диаграммы, включая горизонты и ограничено образующими световых конусов, которые везде имеют один и тот же наклон в 45°. Как видно из диаграммы, попадая под горизонт сигнал неминуемо достигнет следующего горизонта В отличие от чёрной дыры Шварцшильда, частица (сигнал) может избежать столкновения с сингулярностью, благодаря возможности выйти в другую вселенную. Кроме этого, есть возможность через сингулярное кольцо проникнуть во вселенную с «антигравитацией».
В случае «слияния» горизонтов событий диаграмма Пенроуза оказывается «половиной» полной диаграммы. В этом случае вертикальная линия, проведённая по центру рисунка, представляет сингулярность пространства-времени, слева от которой расположены «треугольники» вселенных с «антигравитацией», а справа – «ромбы» областей обычных вселенных и «треугольники» областей между горизонтом и сингулярностью. Остаётся возможность избежать попадания в сингулярность путём выхода в другую вселенную или перехода через сингулярное кольцо. В случае «голой» сингулярности диаграмма Пенроуза вырождается в единственный ромб, разделённый сингулярностью (в виде центральной вертикальной линии) на вселенные с обычной гравитацией и «антигравитацией».
