А́белева катего́рия, категория, обладающая рядом характерных свойств категории всех абелевых групп. Абелевы категории были введены как основа абстрактного построения гомологической алгебры (см. Гротендик. 1961). Категория $\mathfrak{A}$ называется абелевой (Freyd. 1964), если она удовлетворяет следующим аксиомам:

А0. Существует нулевой объект.

А1. Каждый морфизм обладает ядром и коядром.

А2. Каждый мономорфизм является нормальным мономорфизмом; каждый эпиморфизм является нормальным эпиморфизмом.

А3. Для каждой пары объектов существуют произведение и копроизведение.

Часто в определении абелевой категории дополнительно предполагается, что $\mathfrak{A}$ – локально малая слева категория. Для абелевой категории это предположение равносильно локальной малости справа и, следовательно, локальной малости. Копроизведение объектов $A$ и $B$ абелевой категории называется также прямой суммой этих объектов и обозначается $A \oplus B$ или $A+B$.

Примеры абелевых категорий:

1) Категория, двойственная абелевой категории, также является абелевой категорией.

2) Категория ${}_R \mathfrak{M}$ всех левых унитарных модулей над произвольным ассоциативным кольцом $R$ с единицей и всех $R$-модульных гомоморфизмов является абелевой категорией (например, категория всех абелевых групп).

3) Всякая полная подкатегория абелевой категории, содержащая вместе с каждым морфизмом его ядро и коядро и вместе с каждой парой объектов $A, B$ – их произведение и копроизведение, есть абелева категория.

Все малые абелевы категории исчерпываются подкатегориями указанного типа категорий ${}_R\mathfrak{M}$ левых унитарных модулей, а именно, справедлива следующая теорема Митчелла: для всякой малой абелевой категории существует полное точное вложение в некоторую категорию ${}_R\mathfrak{M}$.

4) Всякая категория диаграмм $\mathfrak{F}(\mathfrak{D}, \mathfrak{A})$ со схемой $\mathfrak{D}$ над абелевой категорией $\mathfrak{A}$ является абелевой категорией. В схеме $\mathfrak{D}$ можно выделить множество $C$ соотношений коммутативности, т. е. множество пар $(\varphi, \psi)$ путей $\varphi=\left(\varphi_1, \ldots, \varphi_n\right)$, $\psi=\left(\psi_1, \ldots, \psi_m\right)$ в $\mathfrak{D}$ с общими началом и концом. Тогда полная подкатегория категории $\mathfrak{F}(\mathfrak{D}, \mathfrak{A})$, порождённая всеми такими диаграммами $D: \mathfrak{D} \rightarrow \mathfrak{A}$, что

$$D(\varphi)=D\left(\varphi_1\right) \ldots D\left(\varphi_n\right)=D\left(\psi_1\right) \ldots D\left(\psi_m\right)=D(\psi),$$является абелевой категорией. В частности, если $\mathfrak{D}$ – малая категория, а множество $C$ состоит из всех пар вида $(\alpha \beta, \gamma)$, где $\gamma=\alpha \beta$, то соответствующая подкатегория является абелевой категорией одноместных ковариантных функторов из $\mathfrak{D}$ в $\mathfrak{A}$.

Пусть в малой категории $\mathfrak{D}$ есть нулевой объект; функтор $F :\mathfrak{C} \rightarrow \mathfrak{A}$ называется нормализованным, если он переводит нулевой объект в нулевой объект. Полная подкатегория категории функторов, порождённая нормализованными функторами, является абелевой категорией. B частности, если $\mathfrak{D}$ – категория, объектами которой служат все целые числа и нулевой объект N, а ненулевые неединичные морфизмы образуют последовательность

$$\ldots \longrightarrow(-1) \stackrel{d_{-1}}{\longrightarrow} 0 \stackrel{d_0}{\longrightarrow} 1 \stackrel{d_1}{\longrightarrow} 2 \rightarrow \ldots,$$в которой $d_n d_{n+1}=0$, $n=0, \pm 1, \pm 2, \ldots,$ то соответствующая подкатегория, порождаемая нормализованными функторами, называется категорией комплексов над $\mathfrak{A}$. В категории комплексов определяются аддитивные функторы $Z^n,B^n, H^n$ соответственно $n$-мерных циклов, $n$-мерных граней и $n$-мерной гомологии со значениями в $\mathfrak{A}$ и на их основе развивается аппарат гомологической алгебры.

5) Полная подкатегория $\mathfrak{A}^{\prime}$ абелевой категории называется плотной, если она содержит подобъекты и факторобъекты своих объектов и если в точной последовательности

$$0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$$$B \in \mathrm{O b} \mathfrak{A}^{\prime}$ тогда и только тогда, когда $A, C \in \mathrm{Ob}{ \mathfrak{A}}^{\prime}$. Факторкатегория $\mathfrak{A} / \mathfrak{A}^{\prime}$ строится следующим образом. Пусть $(R, \mu]$ – подобъект прямой суммы $A \oplus B$ с проекциями $\pi_1, \pi_2$, и пусть квадрат

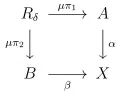коуниверсален (т. е. является корасслоенным произведением). Подобъект $(R, \mu]$ называется $\mathfrak{A}^{\prime}$-подобъектом, если $\operatorname{Coker} \mu \pi_1$, $\operatorname{Ker }\boldsymbol{\beta} \in \mathfrak{A}^{\prime}$. Два $\mathfrak{A}^{\prime}$-подобъекта эквивалентны, если они содержат некоторый $\mathfrak{A}^{\prime}$-подобъект. Множеcтво $H_{\mathfrak{H}/\mathfrak{H}{\prime}}(A,\,B)$ состоит по определению из класса эквивалентных $\mathfrak{A}^{\prime}$-подобъектов. Обычное умножение бинарных отношений согласовано с введённой эквивалентностью, что позволяет построить факторкатегорию $\mathfrak{A} / \mathfrak{A}{ }^{\prime},$ являющуюся абелевой категорией. Точный функтор $T:\mathfrak{A}\rightarrow \mathfrak{A} / \mathfrak{A}{ }^{\prime}$ определяется coпoставлением каждому морфизму $\alpha: A \rightarrow B$ его графика в $A \oplus B$. Подкатегория $\mathfrak{A}^{\prime}$ называется подкатегорией локализации, если функтор $T$ обладает полным унивалентным сопряжением справа функтором $Q: \mathfrak{A} / \mathfrak{A}^{\prime} \rightarrow \mathfrak{A}$.

6) Для всякого топологического пространства $X$ категория левых $G$-модулей над $X$, где $G$ – пучок колец с единицей над $X$, является абелевой категорией.

Во всякой абелевой категории $\mathfrak{A}$ можно ввести частичное суммирование морфизмов таким образом, что $\mathfrak{A}$ станет аддитивной категорией. Поэтому в абелевой категории произведение и копроизведение любой пары объектов совпадают. Более того, в определении абелевой категории можно предполагать существование либо произведений, либо копроизведений. Всякая абелева категория есть бикатегория с единственной бикатегорной структурой. Перечисленные свойства характеризуют абелеву категорию: категория $\mathfrak{A}$ с конечными произведениями является абелевой тогда и только тогда, когда она аддитивна и когда всякий морфизм $\alpha$ имеет ядро и коядро и разлагается в произведение$$\alpha= \text{Coker} \,(\operatorname{ker} \alpha)\, \theta\, \operatorname{ker}\, ( \text{Coker }\alpha),$$в котором $\theta$ – изоморфизм.

Приведённая выше теорема Митчелла обосновывает метод «диаграммного поиска» в абелевой категории: всякое утверждение о коммутативных диаграммах, справедливое во всех категориях левых модулей ${}_R\mathfrak{M}$ и вытекающее из точности некоторых последовательностей морфизмов, справедливо во всех абелевых категориях.

В локально малой абелевой категории $\mathfrak{A}$-подобъекты любого объекта образуют дедекиндову решётку. Если в $\mathfrak{A}$ существуют произведения (или копроизведения) любого семейства объектов, то эта решётка и оказывается полной. Перечисленные условия заведомо выполняются, если в $\mathfrak{A}$ имеется образующий объект $U$ и существуют копроизведения

$$\prod_{i \in I}^* U_i, \quad U_i=U$$для любого множества $I$. Таковы, например, категории Гротендика, эквивалентные факторкатегориям категорий модулей по подкатегориям локализации (теорема Габриеля – Попеску).