Кристаллическая решётка
Кристалли́ческая решётка, определяет обязательную трёхмерную периодичность строения кристаллов. Если при параллельном перемещении кристаллической решётки совместить её узел с атомом или молекулой, то одновременно во всех узлах кристаллической решётки окажутся точно такие атомы или молекулы. Элементарная ячейка кристаллической решётки имеет форму параллелепипеда (рисунок) со сторонами и углами (т. н. параметры решётки). Плотная трёхмерная укладка таких параллелепипедов в параллельном положении и составляет кристалл. В кристаллах без дефектов содержание и расположение атомов или молекул во всех элементарных ячейках одинаково. Вектор между любыми узлами кристаллической решётки является вектором трансляции: структура, перемещённая в параллельном положении на такой вектор, полностью совпадает со структурой до перемещения.
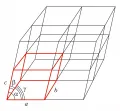 Кристаллическая решётка. Цветом выделена элементарная ячейка.При известной кристаллической решётке существует определённый произвол в выборе элементарной ячейки. Для однозначного выбора ячейки разработаны правила, учитывающие симметрию кристалла. Для триклинных кристаллов (имеющих только центр симметрии или не имеющих его) в качестве рёбер ячейки выбираются не лежащие в одной плоскости векторы , минимальной длины. Элементарная ячейка в этом случае всегда примитивная, т. е. содержит узлы кристаллической решётки только в своих вершинах. В моноклинных кристаллах (имеющих ось симметрии 2-го порядка и/или плоскость симметрии) один вектор направляется вдоль оси 2-го порядка или нормали к плоскости симметрии. В качестве двух других векторов выбираются векторы минимальной длины в перпендикулярной первому вектору плоскости. Из-за того, что первый вектор может быть не минимальным среди некомпланарных двум другим векторам, возможны два типа элементарных ячеек: примитивная и базоцентрированная (бокоцентрированная). В последней дополнительный узел кристаллической решётки находится в середине одной из боковых граней. В ромбических (орторомбических, ортогональных) кристаллах оси 2-го порядка и/или плоскости симметрии определяют 3 взаимно перпендикулярных направления; векторы выбираются вдоль этих направлений. В этом случае возможны 4 типа ячеек: примитивная, базо-, гране- и объёмноцентрированная. В тетрагональных (имеющих ось симметрии 4-го порядка) кристаллах возможны примитивная и объёмноцентрированная ячейки, в тригональных (имеющих ось симметрии 3-го порядка) и гексагональных (имеющих ось симметрии 6-го порядка) кристаллах – примитивная и дважды объёмноцентрированная ячейки, в кристаллах кубической симметрии – примитивная, гране- и объёмноцентрированная ячейки. Так, с учётом симметрии кристаллов в их кристаллических решётках определяются 14 типов решёток Браве.
Кристаллическая решётка. Цветом выделена элементарная ячейка.При известной кристаллической решётке существует определённый произвол в выборе элементарной ячейки. Для однозначного выбора ячейки разработаны правила, учитывающие симметрию кристалла. Для триклинных кристаллов (имеющих только центр симметрии или не имеющих его) в качестве рёбер ячейки выбираются не лежащие в одной плоскости векторы , минимальной длины. Элементарная ячейка в этом случае всегда примитивная, т. е. содержит узлы кристаллической решётки только в своих вершинах. В моноклинных кристаллах (имеющих ось симметрии 2-го порядка и/или плоскость симметрии) один вектор направляется вдоль оси 2-го порядка или нормали к плоскости симметрии. В качестве двух других векторов выбираются векторы минимальной длины в перпендикулярной первому вектору плоскости. Из-за того, что первый вектор может быть не минимальным среди некомпланарных двум другим векторам, возможны два типа элементарных ячеек: примитивная и базоцентрированная (бокоцентрированная). В последней дополнительный узел кристаллической решётки находится в середине одной из боковых граней. В ромбических (орторомбических, ортогональных) кристаллах оси 2-го порядка и/или плоскости симметрии определяют 3 взаимно перпендикулярных направления; векторы выбираются вдоль этих направлений. В этом случае возможны 4 типа ячеек: примитивная, базо-, гране- и объёмноцентрированная. В тетрагональных (имеющих ось симметрии 4-го порядка) кристаллах возможны примитивная и объёмноцентрированная ячейки, в тригональных (имеющих ось симметрии 3-го порядка) и гексагональных (имеющих ось симметрии 6-го порядка) кристаллах – примитивная и дважды объёмноцентрированная ячейки, в кристаллах кубической симметрии – примитивная, гране- и объёмноцентрированная ячейки. Так, с учётом симметрии кристаллов в их кристаллических решётках определяются 14 типов решёток Браве.
