Скаля́рное произведе́ние (иногда называют внутренним произведением), операция над двумя векторами, результатом которой является число (скаляр). Обозначениями скалярного произведения являются: $\vec{a}\,\vec{b}$, $\vec{a}\cdot\vec{b}$, $(\vec{a},\,\vec{b})$, $\langle\vec{a},\,\vec{b}\rangle$. Последнее является обозначением П. Дирака, которое применяется в квантовой механике.

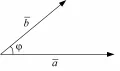Геометрический смысл скалярного произведения.Геометрический смысл скалярного произведения.На плоскости и в трёхмерном пространстве (пространства $\mathbb{R}^2$ и $\mathbb{R}^3$), для которых угол между двумя векторами определяется геометрически, скалярное произведение двух ненулевых векторов $\vec{a}$ и $\vec{b}$ есть число, равное произведению длин этих векторов на косинус угла $\varphi$ между ними (см. рисунок): $(\vec{a},\,\vec{b})=\left|\vec{a}\right||\vec{b}|\cos{\varphi}.$В общем случае скалярное произведение $(\vec{a},\,\vec{b})$ ненулевых векторов $\vec{a}$ и $\vec{b}$ вещественного векторного пространства есть функция от $\vec{a}$ и $\vec{b}$ с вещественными значениями, удовлетворяющая следующим требованиям:

1) для любого вектора $\vec{a}$ выполнено неравенство $(\vec{a},\,\vec{a})\geqslant 0$, причём $(\vec{a},\,\vec{a})=0$ только в случае, если $\vec{a}=\vec{0}$ – нулевой вектор;

2) для любых векторов $\vec{a}$ и $\vec{b}$ справедливо равенство $(\vec{a},\,\vec{b})=(\vec{b},\,\vec{a})$ (симметрия);

3) для любых векторов $\vec{a}$, $\vec{b}$, $\vec{c}$ и чисел $m$, $n$ выполнено равенство $(m\vec a+n\vec b,\,c)=m(\vec a,\,\vec c)+n(\vec b,\,\vec c)$ (линейность по первой компоненте); аналогична линейность по второй компоненте.

Длина вектора $\vec{a}$ вычисляется по формуле $$|\vec{a}|=\sqrt{(\vec{a},\,\vec{a})}.$$Угол $\varphi$ между векторами $\vec{a}$ и $\vec{b}$ определяется с помощью формулы $$\cos{\varphi}=\frac{(\vec{a},\,\vec{b})}{|\vec{a}|\,|\vec{b}|}.$$$n$-мерное вещественное линейное пространство с определённым в нём скалярным произведением называется евклидовым пространством.

В комплексном векторном пространстве скалярное произведение $(\vec{a},\,\vec{b})$ ненулевых векторов $\vec{a}$ и $\vec{b}$ задаётся функцией от $\vec{a}$ и $\vec{b}$ с комплексными значениями, удовлетворяющей следующим требованиям:

1) для любого вектора $\vec{a}$ выполнено неравенство $(\vec{a},\,\vec{a})\geqslant0$, причём $(\vec{a},\,\vec{a})=0$ только в случае, если $\vec{a}=\vec{0}$ – нулевой вектор;

2) для любых векторов $\vec{a}$ и $\vec{b}$ справедливо равенство$(\vec{a},\,\vec{b})=\overline{(\vec{b},\,\vec{a})}$ (симметрия с переходом к сопряжённому);

3) для любых векторов $\vec{a}$, $\vec{b}$, $\vec{c}$ и чисел $m$, $n$ выполнено равенство $(m\vec a+n\vec b,\,c)=m(\vec a,\,\vec c)+n(\vec b,\,\vec c)$ (линейность по первой компоненте); аналогична линейность по второй компоненте.

$n$-мерное линейное пространство над полем комплексных чисел с определённым в нём скалярным произведением называется унитарным (эрмитовым) пространством.

Длина вектора в комплексном векторном пространстве определяется аналогично длине вектора в вещественном векторном пространстве, понятие угла между векторами не вводится.

В евклидовом и унитарном пространствах для любых векторов $\vec{a}$ и $\vec{b}$ выполняется неравенство Коши – Буняковского: $$|(\vec{a},\,\vec{b})|^2\leqslant(\vec{a},\,\vec{a})(\vec{b},\,\vec{b}).$$Как правило, скалярное произведение векторов $\vec{a}=\{x_1, x_2,\ldots,x_n\}$ и $\vec{b}=\{y_1, y_2,\ldots,y_n\}$ в $n$-мерном евклидовом пространстве определяется по формуле $$(\vec{a},\,\vec{b})=x_1y_1+x_2y_2+\ldots+\,\ x_ny_n,$$а в $n$-мерном унитарном пространстве – по формуле: $$(\vec{a},\,\vec{b})=x_1\overline{y_1}+x_2\overline{y_2}+...+ x_n\overline{y_n}.$$В общем случае в евклидовом пространстве с базисом $\vec{e}_1,\vec{e}_2,\ldots,\vec{e}_n$ скалярное произведение векторов $\vec{a}=x_1{\vec{e}}_1+x_2{\vec{e}}_2+\ldots+x_n{\vec{e}}_n$, $\vec{b}=y_1{\vec{e}}_1+y_2{\vec{e}}_2+\ldots+y_n{\vec{e}}_n$ определено формулой $$(\vec{a},\,\vec{b})=\sum_{i=1}^{n}\sum_{j=1}^{n}{g_{ij}x_iy_j},$$а в унитарном пространстве – формулой $$(\vec{a},\,\vec{b})=\sum_{i=1}^{n}\sum_{j=1}^{n}g_{ij}x_i\overline{y_j},$$где $g_{ij}$ – элементы симметричной положительно определённой матрицы Грама.

Скалярное произведение также вводится в бесконечномерных пространствах функций. Например, для функций $f$ и $g$ одной и двух переменных $$\begin{aligned}(f,\, g)&=\int\limits_{a}^{b}K(x)f(x)g(x)\,dx,\\ (f,\, g)&=\int\limits_{a}^{b}\!\!\int\limits_{c}^{d}K(x,y)f(x)g(y)\,dxdy,\end{aligned}$$где $K$ – положительно определённая функция. В частности, скалярное произведение интегрируемых функций на отрезке $L_2[a,b]$ можно определить по формуле $$(f,\, g)=\displaystyle\int\limits_{a}^{b}f(x)g(x)\,dx.$$Скалярное произведение комплекснозначных непрерывных функций на отрезке $[a,b]$ определяется по формуле $$\displaystyle (f,\, g)=\int\limits_{a}^{b}f(x)\overline{g(x)}\,dx.$$Вещественное или комплексное линейное пространство с определённым в нём скалярным произведением называет предгильбертовым.