Нуль

Нуль (от лат. nullus – никакой), число, обладающее тем свойством, что любое число при сложении с ним не меняется, обозначается символом $0$. Произведение любого числа $a$ на нуль равно нулю: $a·0=0·a=0$. Если произведение двух действительных или комплексных чисел равно нулю, то хотя бы один из сомножителей равен нулю: из $ab=0$ следует, что или $a=0$, или $b=0$. Деление на нуль невозможно.

В коммутативной аддитивно записываемой группе нулём называется элемент 0, для которого $a+0=0+a=a$, где $a$ – любой элемент группы. В кольце нуль определяется аналогично; там для нуля всегда выполняется равенство $a·0=0·a=0$. Однако, если произведение двух элементов кольца равно нулю, то из этого не следует, что один из сомножителей равен нулю; если $ab=0$, причём $a≠0$ и $b≠0$, то элементы $a$ и $b$ называются делителями нуля.

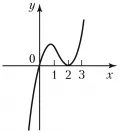
Нуль функции – точка $x_0$, в которой заданная функция $f(x)$ обращается в нуль, т. е. $f(x_0)=0$. Например, для функции $3x-2$ нулём является точка $x_0=2/3$. Некоторые функции не имеют нуля, например, $e^x$, у других, например, у тригонометрических, бесконечное множество нулей. Нули функции $f(x)$ – то же самое, что корни уравнения $f(x)=0.$ Число $x_0$ называется $m$-кратным нулём (нулём порядка $m$, $m$ – натуральное число) многочлена $P$, если x₀ – $m$-кратный корень уравнения $P(x_0)=0$, т. е. многочлен $P(x)=(x-x_0)^mQ(x)$, где многочлен $Q(x_0)≠0$. При $m=1$ корень называется простым. Нули функции одного переменного $f(x)$являются точками пересечения её графика с осью абсцисс или точками касания графика и этой оси. Например, функция $f(x)=x^3- 4x^2+ 4x$ (рис.) имеет два нуля – простой (в точке $x_1=0$) и двукратный (в точке $x_2=2$); функция $f(x)=\sin x$ имеет счётное множество простых нулей – в точках $0,\pm π ,\pm 2π ,\ldots$

Нули аналитической функции $f(z)$ одного комплексного переменного $z$ являются изолированными точками. Для каждого нуля $z_0$ существует натуральное число $m$ – порядок нуля – такое, что $f(z_0)=0$, $f' (z_0)=0, \ldots$, $f^{(m-1)}(z_0)=0$, но $f^{(m)}(z_0)≠0$; например, для нуля функции $1-\cos z$ порядок $m=2$. Напротив, аналитические функции$f(z_1,\ldots,z_n)$ многих комплексных переменных не могут иметь изолированных нулей.