Ма́ятник, механическая система, совершающая колебательное движение под действием т. н. восстанавливающей силы – силы, стремящейся возвратить систему в положение равновесия.

Роль восстанавливающей силы может играть сила тяжести. В этом случае маятник представляет собой массивное тело, способное вращаться вокруг горизонтальной (или наклонной) оси, не проходящей через его центр масс.

Рис. 1. Схемы маятников.Рис. 1. Схемы маятников.Если расстояние между осью вращения и центром масс меняется во время колебаний, маятник называется параметрическим, если это расстояние постоянно – физическим (рис. 1, а). Физический маятник называется математическим, если расстояние от точек колеблющегося тела до оси вращения велико по сравнению с размерами тела, а масса нити или стержня, соединяющих колеблющееся тело с осью вращения, пренебрежимо мала по сравнению с массой тела (т. е. тело можно считать материальной точкой, рис. 1, б). Достаточным условием для того, чтобы маятник можно было назвать математическим, является малость размеров проекции тела на плоскость, перпендикулярную оси качания, по сравнению с расстояниями от точек этой проекции до оси. Если такой маятник совершает колебания в одной плоскости и амплитуда колебаний достаточно мала, то колебания (в пренебрежении трением) являются гармоническими, их период ${T_0}$ не зависит от амплитуды и определяется выражением:

$${{T_0=2\pi \sqrt{\frac{l}{g\:\textrm{cos}\:\varphi }},}}\tag{1}$$где ${l}$ – длина математического маятника (расстояние от оси вращения до колеблющейся массы), ${g}$ – ускорение свободного падения, ${φ}$ – угол отклонения плоскости качания от вертикали. В частном случае колебаний в вертикальной плоскости формула приобретает вид:

$${{T_0=2\pi \sqrt{\frac{l}{g}},}}\tag{2}$$Для физического маятника период малых колебаний в отсутствие трения определяется тем же выражением, но на место ${l}$ ставится величина ${l_{пр}}$, называемая приведённой длиной физического маятника: ${l_{пр}=\frac{J_0}{ml_0}},$ где ${m}$ – масса физического маятника, ${J_0}$ – его момент инерции относительно оси вращения, ${l_0}$ – расстояние между осью вращения и центром масс маятника. В общем случае период плоских колебаний маятника зависит от амплитуды колебаний.

В 1657 г. Х. Гюйгенс теоретически обосновал и затем сконструировал часовой маятник, период колебаний которого не зависел от амплитуды. В предложенном механизме плоское движение математического маятника совершалось не по дуге окружности, а по дуге циклоиды (циклоидальный маятник). Позднее было найдено, что реализовать почти полную независимость периода колебаний от амплитуды можно технически более просто. Для этого физический маятник прикрепляют к вертикальной упругой пластине, изгиб которой при отклонении маятника практически устраняет нелинейность зависимости возвращающего момента силы тяжести от угла отклонения. Этот приём используется в современных маятниковых часах.

Точка физического маятника, находящаяся на прямой, проведённой от оси качания через центр масс, и расположенная на расстоянии ${l_{пр}}$ от оси, называется центром качания. Если через центр качания провести новую ось качания, параллельную прежней, то период колебаний физического маятника останется неизменным, а положение прежней оси станет новым центром качания.

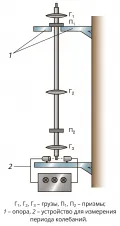Рис. 2. Схема оборотного маятника.Рис. 2. Схема оборотного маятника.Это свойство используется в оборотном маятнике (рис. 2), применяемом в гравиметрии. Он представляет собой стержень с одним или несколькими подвижными грузами и двумя призмами, поочерёдно помещаемыми на опору, служащую осью качания маятника. Перемещая грузы, добиваются равенства периодов малых колебаний маятника при опоре на каждую из призм. Таким образом, заданное расстояние между призмами будет равняться ${l_{пр}}$ полученного маятника, что по измеренному периоду колебаний позволяет определить ускорение свободного падения с точностью около ${10^{–5} \,м/с^{2}}$.

Пространственное положение плоскости колебаний математического маятника остаётся практически неизменным, что позволяет заметить движение плоскости колебаний маятника относительно поверхности Земли вследствие суточного вращения последней (см. Маятник Фуко). При использовании определённого типа подвеса (например, сферического или карданового шарнира) центр масс маятника может также совершать колебания по сферической поверхности, обращённой выпуклостью вниз (сферический маятник). Частным случаем сферического маятника является конический маятник, в котором центр масс маятника описывает горизонтальную окружность.

Рис. 3. Модель часов с маятниковым механизмом Галилео Галилея. 1921. Конструктор Инкерман Роджерс. Музей науки, Лондон.Рис. 3. Модель часов с маятниковым механизмом Галилео Галилея. 1921. Конструктор Инкерман Роджерс. Музей науки, Лондон.В качестве восстанавливающей силы может выступать также сила упругости. В этом случае маятник представляет собой груз, прикреплённый к упругому элементу. При отклонении груза от положения равновесия наблюдаются поступательные колебания груза, возникающие при сжатии и растяжении лёгкой пружины или другого упругого тела (пружинный маятник), или вращательные колебания груза под действием момента сил, возникающих при закручивании нити, пружины или стержня с пренебрежимо малым моментом инерции (крутильный маятник). Если упругий элемент таких маятников подчиняется закону Гука, то в отсутствие трения колебания маятника являются гармоническими. Их период ${T}$ не зависит от амплитуды колебаний: для пружинного маятника ${T=2\pi \sqrt{m/k}},$ где ${m}$ – масса груза, $\textit{k}$ – жёсткость пружины; для крутильного маятника ${T=2\pi \sqrt{J/f}},$ где ${J}$ – момент инерции груза относительно оси вращения, ${f}$ – модуль кручения упругого элемента.

Рис. 4. Маятниковый миограф. Германия. Ок. 1900. Сконструирован Германом Гельмгольцем ок. 1850 для измерения скорости нервных импульсов лягушки. Музей науки, Лондон.Рис. 4. Маятниковый миограф. Германия. Ок. 1900. Сконструирован Германом Гельмгольцем ок. 1850 для измерения скорости нервных импульсов лягушки. Музей науки, Лондон.Различные маятниковые приборы широко применяются в технике. Наиболее известный маятниковый прибор – механические часы, в которых используется физический или крутильный маятник. Крутильный маятник является также основным элементом крутильных весов, а пружинный маятник – акселерометра. Маятниковые приборы применяются в сейсмографах, центробежных регуляторах скорости; с их помощью измеряют моменты инерции тел, скорости пуль и снарядов (баллистические маятники), с помощью наклонных маятников (физические маятники, в которых груз-шарик катается по наклонной плоскости) исследуют трение качения и т. д.