Ква́нтовая электродина́мика (КЭД, спинорная электродинамика), квантовая теория электромагнитного взаимодействия заряженных частиц, одного из четырёх видов фундаментальных взаимодействий, известных в природе. В более узком значении КЭД – это квантовая теория взаимодействия электромагнитного поля Максвелла и электрон-позитронного поля Дирака (спинорного поля).

Исторически КЭД была первым чётко сформулированным разделом квантовой теории поля (КТП). Она сложилась в конце 1920-х гг. на базе квантовой теории излучения и квантовой теории спинорного поля Дирака. КЭД количественно объясняет эффекты взаимодействия излучения с веществом (испускание, поглощение и рассеяние света), а также описывает взаимодействие между заряженными частицами путём обмена квантом взаимодействия – фотоном, частицей с нулевой массой и спином 1. В основе современной формулировки КЭД лежит КТП, содержащая два взаимодействующих релятивистских поля: электромагнитное поле, характеризуемое действительным четырёхмерным векторным потенциалом $A_\mu(x)$ ($\mu=0,1,2,3$; $x$ – пространственно-временнáя координата), и поле Дирака, описываемое комплексным лоренцевым спинором $\psi_\beta(x)$ ($\beta=1,2,3,4$). В случае КЭД электромагнитное взаимодействие характеризуется лагранжианом $L(x)=-\frac{1}{4}F_{\mu \nu}F^{\mu \nu}+ \bar{\psi}(i \gamma^\mu \partial/\partial x^\mu -m)\psi+e\bar{\psi}\gamma^\mu A_\mu \psi$, $\quad(*)$

где $e$ – заряд электрона, $m$ – масса электрона, $\gamma^\mu$  – матрицы Дирака, $F_{\mu \nu}= \partial A_\nu /\partial x^\mu-\partial A_\mu/\partial x^\nu$ – тензор напряжённости электромагнитного поля.

Лагранжиан $(*)$ описывает всю совокупность электромагнитных явлений. Безразмерной константой, характеризующей интенсивность взаимодействия, является постоянная тонкой структуры $\alpha=e^2/\hbar c \sim 1/137$ [точнее $\alpha^{-1}=137,035981(12)$]. Лагранжиан (*) инвариантен (симметричен) относительно изменения фазы спинорного поля [группа инвариантности $(U)1$] и является примером абелевой калибровочной теории. КЭД является составной частью Стандартной модели фундаментальных взаимодействий, описывающей сильные, слабые и электромагнитные взаимодействия на основе единого принципа локальной калибровочной симметрии.

Квантование системы полей $A$, $\psi$, взаимодействие которых описывается лагранжианом (*), приводит к квантовой теории электромагнитного взаимодействия, причём поле Максвелла $A_\mu$ квантуется на основе статистики Бозе – Эйнштейна, а поле Дирака $\psi$ – на основе статистики Ферми – Дирака. Согласно общим положениям КТП, поля $A_\mu$, $\psi$ после квантования становятся операторами, удовлетворяющими определённым перестановочным соотношениям и действующими на вектор состояния системы. Эти операторы удовлетворяют также связанной системе дифференциальных уравнений, которые вместе с уравнением Шрёдингера для вектора состояния образуют систему уравнений движения КЭД.

Поскольку система уравнений движения КЭД не допускает точного решения, её решают приближённо методом теории возмущений по малому безразмерному параметру $\alpha$. Наглядное графическое изображение этой теории дают диаграммы Фейнмана. На этих диаграммах линии изображают распространение частиц, вершины – процесс локального взаимодействия. 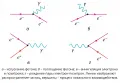Рис. 1. Диаграммы Фейнмана, описывающие реакции, в которых число частиц не сохраняется.Рис. 1. Диаграммы Фейнмана, описывающие реакции, в которых число частиц не сохраняется.Диаграммам соответствуют определённые математические выражения, задаваемые правилами Фейнмана, которые позволяют вычислять амплитуды вероятностей перехода систем, состоящих из фотонов ($\gamma$), электронов ($e^-$), позитронов ($e^+$) и других частиц, из одного состояния в другое. Вероятность перехода, как и в квантовой механике, даётся квадратом модуля амплитуды вероятности. Однако в отличие от квантовой механики, число частиц в реакциях не сохраняется, возможны процессы рождения, распада, аннигиляции частиц, а также испускание и поглощение фотонов (рис. 1).

Первый эффект, который объяснила КЭД, – лэмбовский сдвиг уровней энергии атома. КЭД описывает также такие процессы, как комптоновское рассеяние (эффект Комптона), тормозное излучение, аннигиляция и рождение частиц и др. (рис. 2). Относительная погрешность вычислений составляет величину порядка $\alpha$. Для увеличения точности необходимо учесть высшие члены теории возмущений – т. н. радиационные поправки, соответствующие вкладам от таких переходов, которые в промежуточных состояниях содержат дополнительные виртуальные частицы – виртуальные фотоны, электроны и позитроны. 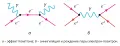Рис. 2. Диаграммы Фейнмана, описывающие эффект Комптона, а также аннигиляцию и рождение пар частиц.Рис. 2. Диаграммы Фейнмана, описывающие эффект Комптона, а также аннигиляцию и рождение пар частиц.Однако соответствующие матричные элементы, представляемые интегралами по четырёхмерным импульсам виртуальных частиц, как правило, расходятся в области больших импульсов и приводят к бесконечностям. Проблема расходимости в течение многих лет препятствовала вычислению радиационных поправок в КЭД и развитию КТП в целом. Она была решена во 2-й половине 1940-х гг. с помощью метода перенормировок, в котором все УФ-расходимости в КЭД можно представить в виде вкладов, перенормирующих характеристики электрона – его массу $m$ и заряд $e$. Бесконечный характер таких перенормировок не приводит к физическим противоречиям вследствие невозможности наблюдать неперенормированные, «голые» значения $m_0$ и $e_0$. Первой успешной демонстрацией плодотворности идеи об устранении УФ-расходимостей с помощью бесконечных перенормировок была работа X. Бете (1947) по нерелятивистскому расчёту лэмбовского сдвига уровней в атоме водорода. Ковариантная теория возмущений (Томонага Синъитиро, Дж. Швингер, P. Фейнман, 1946–1949) позволила создать регулярный метод устранения расходимостей в КЭД и вычислить низшие радиационные поправки к основным эффектам, например к магнитному моменту электрона. В 1-й половине 1950-х гг. была разработана (Ф. Дайсон, А. Салам, Н. Н. Боголюбов и др.) общая теория перенормировок и для класса перенормируемых взаимодействий построена перенормированная теория возмущений.

Радиационные поправки к процессам с участием заряженных частиц имеют также ИК-расходимости, связанные с дальнодействующим характером электромагнитного взаимодействия. Однако ИК-расходимости отсутствуют в сечении инклюзивных процессов, в котором суммируются вероятности переходов в состояния с произвольным числом «мягких» фотонов (экспериментально такие состояния нельзя отличить от исходного из-за конечной разрешающей способности регистрирующих приборов).

Хорошее согласие теоретических расчётов КЭД с экспериментом может быть проиллюстрировано на примере вычисления радиационных поправок к аномальному магнитному моменту электрона. Магнитный момент – величина, обусловливающая взаимодействие покоящейся частицы с внешним магнитным полем. Из квантовой теории электрона Дирака следует, что электрон обладает магнитным моментом, равным магнетону Бора $\mu_Б=e\hbar/2mc$. В КЭД к этому выражению возникают поправки, получившие название аномального магнитного момента. Они пропорциональны $\alpha$ в степенях 2, 3 и т. д. и обязаны своим происхождением рождению виртуальных частиц в вакууме. Простейшая диаграмма Фейнмана, соответствующая возникновению аномального магнитного момента электрона, изображена на рис. 3, б. Она была вычислена Дж. Швингером в 1948 г. и даёт значение . На 2008 г. аномальный магнитный момент электрона в КЭД вычислен с высокой точностью: $\mu_{теор}=\mu_Б(1+(\alpha/2\pi)-0,328478(\alpha/\pi)^2+1,184175(\alpha/\pi)^3+\dots) = 1,001159652306(111)\mu_Б$ и находится в согласии с экспериментальным значением

$\mu=\mu_Б(1+\alpha/2\pi)$,

определённым с точностью $10^{–12}$. Соответствие между расчётным и экспериментальными значениями (порядка $10^{–10}$) является рекордным в физике. Точность сравнения теории с экспериментом определяется погрешностью в значении $\alpha$, определённом с помощью эффекта Джозефсона. На этом уровне точности оказываются несущественными теоретические квантовополевые поправки за счёт эффектов сильного и слабого взаимодействий и эффектов, выходящих за рамки КЭД, а также радиационные поправки порядка $\alpha^4$.

Характерным эффектом, который объясняется КЭД, является рассеяние света на свете (рис. 3, в). В классической электродинамике этот эффект вообще не рассматривается, т. к. электромагнитные волны не взаимодействуют друг с другом. 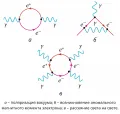Рис. 3. Диаграммы Фейнмана для эффектов, которые можно объяснить только в рамках квантовой электродинамики.Рис. 3. Диаграммы Фейнмана для эффектов, которые можно объяснить только в рамках квантовой электродинамики.В КЭД это становится возможным благодаря наличию флуктуаций вакуума, в результате которых появляется взаимодействие между фотонами, т. е. нарушается принцип суперпозиции электромагнитных волн.

Для других эффектов КЭД – аннигиляции и рождения пары электрон – позитрон, дельбрюковского рассеяния фотонов электромагнитным полем ядра и других – также характерно отличное согласие теории с экспериментом. Однако по сравнению с аномальным магнитным моментом уровень соответствия в них не столь высок либо из-за меньшей точности эксперимента, либо вследствие того, что оказывается более существенным учёт эффектов, выходящих за рамки КЭД. Так, например, экспериментальное значение величины сверхтонкого расщепления уровня 1s_1/2 в атоме водорода известно с точностью, достигающей 13 порядков, тогда как теоретические расчёты дают здесь лишь 7 знаков, причём уже с учётом конечных размеров протона. Величина лэмбовского сдвига в атоме водорода известна из опыта с точностью 10^–7, а согласующееся с ней теоретическое значение имеет погрешность на уровне 10^–6, причём вклад эффектов, выходящих за рамки КЭД, достигает порядка 10^–5.

Эффект поляризации вакуума за счёт рождения виртуальных электрон-позитронных пар экспериментально проявляется в зависимости постоянной тонкой структуры от переданного импульса частиц, участвующих во взаимодействии. В низшем порядке по $\alpha$ он определяется диаграммой Фейнмана (рис. 3, а) и ведёт к логарифмической зависимости эффективной константы от импульса:

$\alpha(p^2)=\frac{\alpha(0)}{1-\frac{\alpha(0)}{3\pi}\lg \left(\frac{p^2}{m^2} \right)}$,

что получило подтверждение в измерениях на Большом электрон-позитронном коллайдере в ЦЕРНе (Женева).

Экспериментальные данные по всем без исключения эффектам КЭД прекрасно согласуются с теоретическими значениями в тех случаях, когда другие виды взаимодействий в этих эффектах оказываются несущественными либо поддаются учёту. Этот факт имеет принципиальное значение как для КЭД, так и для КТП в целом. Он свидетельствует о том, что основные положения современной локальной (калибровочной) КТП, а также динамическая основа КЭД, соответствующая локально калибровочному лагранжиану взаимодействия, оказываются справедливыми во всей области, доступной современному эксперименту.