Парадо́кс Алле́, мысленный эксперимент в отношении выбора между лотереями, результаты которого противоречат предсказаниям теории ожидаемой полезности.

М. Алле – французский учёный, лауреат премии памяти А. Нобеля по экономическим наукам 1988 г., опубликовал в 1953 г. статью «Рациональное поведение человека перед лицом риска. Критика постулатов и аксиом американской школы» («Le comportement de l'homme rationnel devant le risque: Critique des postulats et axiomes de l'Ecole Americaine»). Парадокс Алле является первым и одним из наиболее известных примеров противоречия индивидуального выбора теории ожидаемой полезности.

В эксперименте заданы две пары лотерей: $L_{1}$ и $L_{2}$, и $L_{3}$ и $L_{4}$. Участники осуществляют последовательный выбор наиболее предпочитаемой лотереи из каждой пары.

Три денежных приза (0 долл., 1 млн долл., 5 млн долл.) образуют множество исходов. Лотерея $L_{1}$ задана вырожденным распределением; при выборе данной лотереи в первой паре детерминированный (предопределённый) выигрыш составит 1 млн долл. При выборе $L_{2}$ выигрыш составит 5 млн долл. с вероятностью 0,1 и 1 млн долл. с вероятностью 0,89, а с вероятностью 0,01 выигрыш равен 0.

Во второй паре лотерей отсутствует альтернатива с детерминированным выигрышем. При выборе лотереи $L_{3}$ потенциальный выигрыш равен 5 млн долл. с вероятностью 0,1 и 0 – с вероятностью 0,9. В лотерее $L_{4}$ вероятность приза несколько выше – 0,11, но приз составляет 1 млн долл., а с вероятностью 0,89 выигрыш равен 0.

Многие участники эксперимента делают выбор в пользу альтернативы $L_1$ в первой паре лотерей и в пользу игры $L_3$ во второй паре. Данный выбор может быть представлен в вероятностном треугольнике.

Пусть $\mathcal{p} _{1}$ – вероятность выигрыша 0 долл., $\mathcal{p} _{2}$ – вероятность выигрыша 1 млн долл., а $\mathcal{p} _{3}$ –вероятность выигрыша 5 млн долл.; выполнено $p_1+p_2+p_3=1$. В качестве примера можно изобразить вероятностный треугольник на плоскости $(p_1, p_3)$. На рис. 1 по горизонтальной оси отложена вероятность наихудшего (0 долл.) исхода $\mathcal{p} _{1}$, по вертикальной – вероятность наилучшего (5 млн долл.) исхода $\mathcal{p} _{3}$. Вдоль горизонтальной оси сумма вероятностей $p_1+p_2=1$, вдоль вертикальной оси выполнено $p_3+p_2=1$, а для любой точки гипотенузы выполнено $p_1+p_3=1$. Любая точка в вероятностном треугольнике соответствует некоторой лотерее $L=(p_1, p_2, p_3)$, где $p_2=1-p_1-p_3$. Например, точка А на графике соответствует $L_{1}$ из первой пары лотерей: в данной лотерее $p_1=p_3=0$. Точка В соответствует лотерее $L_{2}$, точки C и D – лотереям $L_{3}$ и $L_{4}$ соответственно. Точки A, B, C и D образуют параллелограмм. Для иллюстрации противоречия выбора альтернатив $L_{1}$ и $L_{3}$ предсказаниям теории ожидаемой полезности можно изобразить в вероятностном треугольнике в осях $(p_1, p_3)$ кривые безразличия функции ожидаемой полезности.

Рис. 1. Вероятностный треугольник и кривые безразличия функции ожидаемой полезности.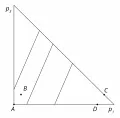Рис. 1. Вероятностный треугольник и кривые безразличия функции ожидаемой полезности.Кривые безразличия представляют пары $(p_1, p_3)$, соответствующие лотереям с одинаковым значением ожидаемой полезности. В теории ожидаемой полезности кривые безразличия функции ожидаемой полезности являются прямыми и параллельными линиями. В осях $(p_1, p_3)$ эти кривые имеют положительный наклон. Карта кривых безразличия на рис. 1 представлена параллельными отрезками. Кривые, лежащие левее и выше, соответствуют более высокой ожидаемой полезности.

Если участник эксперимента выбирает лотерею $L_{1}$ по сравнению с лотереей $L_{2}$ в первой паре лотерей, то точка А лежит на кривой безразличия, которая соответствует более высокому значению ожидаемой полезности, чем кривая, на которой лежит точка B. На рис. 2 кривые безразличия, проходящие через точки А и В, показаны относительно крутыми отрезками.

Аналогично выбор альтернативы $L_{3}$ из второй пары лотерей означает, что точка C лежит на кривой безразличия, соответствующей более высокому значению ожидаемой полезности, чем кривая, на которой лежит точка D. Кривые безразличия, проходящие через точки C и D, представлены в виде более пологих линий (см. рис. 2).

Наблюдаемый выбор несовместим с параллельными кривыми безразличия. В соответствии с теорией ожидаемой полезности выбор $L_{1}$ в первой паре означает, что кривая безразличия, проведённая через точку D, должна представлять более высокий уровень ожидаемой полезности, чем кривая, которой принадлежит точка С. Следовательно, из второй пары лотерей должна быть выбрана $L_{4}$. Точно так же в рамках теории ожидаемой полезности выбор $L_{2}$ в первой паре предполагал бы выбор $L_{3}$ во второй.

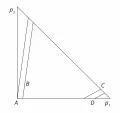Рис. 2. Парадокс Алле.Рис. 2. Парадокс Алле.Парадокс Алле не является изолированным примером и относится к семейству парадоксов, выявляющих систематическое нарушение предсказаний теории ожидаемой полезности в экспериментах. В альтернативных моделях выбора в условиях риска форма кривых безразличия отлична от параллельных прямых линий, что позволяет получить экспериментально наблюдаемые результаты в теории.