Многоуго́льник, замкнутая ломаная линия. Точнее, многоугольник – линия, которая получается, если взять $n$ точек $A_1,A_2,...,A_n$ и соединить прямолинейными отрезками каждую из них с последующей, а последнюю – с первой (рис. 1, а, б). Точки $A_1,A_2,...,A_n$ называются вершинами многоугольника, а отрезки $A_1A_2, A_2A_3,...,A_{n–1}A_n,A_nA_1$ – его сторонами. Далее рассматриваются только плоские многоугольники (т. е. предполагается, что многоугольник лежит в одной плоскости). Многоугольник может сам себя пересекать, причём точки самопересечения могут не быть его вершинами (рис. 1, в).

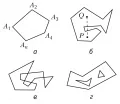Рис. 1. Примеры многоугольников.Рис. 1. Примеры многоугольников.Если многоугольник не пересекает сам себя (например, рис. 1, а и 1, б), то он разделяет совокупность всех точек плоскости, не лежащих на нём, на две части – конечную (внутреннюю) и бесконечную (внешнюю) в том смысле, что если две точки принадлежат одной из этих частей, то их можно соединить одну с другой ломаной, не пересекающей многоугольник, а если разным частям, то нельзя. Несмотря на очевидность этого утверждения, строгий его вывод из аксиом геометрии довольно труден (т. н. теорема Жордана о многоугольниках). Внутренняя по отношению к многоугольнику часть плоскости имеет определённую площадь. Если многоугольник – самопересекающийся, то он выделяет на плоскости некоторое число кусков, из которых один бесконечный (называемый внешним по отношению к многоугольнику), а остальные – конечные односвязные (называемые внутренними), причём граница каждого из них есть некоторый самонепересекающийся многоугольник, стороны которого суть целые стороны или части сторон, а вершины – вершины или точки самопересечения исходного многоугольника. Если каждой стороне многоугольника приписать направление, т. е. указать, какую из двух определяющих её вершин считать её началом, а какую – концом, и притом так, чтобы начало каждой стороны было концом предыдущей, то получится (замкнутый) многоугольный путь, или ориентированный многоугольник. Площадь области, ограниченной самопересекающимся ориентированным многоугольником, считается положительной, если контур многоугольника обходит эту область против часовой стрелки, т. е. внутренность многоугольника остаётся слева от идущего по этому пути, и отрицательной – в противоположном случае.

Пусть многоугольник – самопересекающийся и ориентированный. Если из точки, лежащей во внешней по отношению к нему части плоскости, провести прямолинейный отрезок к точке, лежащей внутри одного из его внутренних кусков, и многоугольник пересечёт этот отрезок $p$ раз слева направо и $q$ раз справа налево, то число $p-q$ (целое положительное, отрицательное или нуль) не зависит от выбора внешней точки и называется коэффициентом этого куска. Сумма обычных (без знака) площадей этих кусков, умноженных на коэффициент кусков, считается площадью рассматриваемого ориентированного многоугольника.

Сумма внутренних углов любого самонепересекающегося многоугольника с $n$ сторонами равна $(n-2)180°$. Многоугольник называется выпуклым (рис. 1, а), если никакая сторона многоугольника, будучи неограниченно продолженной, не разрезает его на две части. Выпуклый многоугольник характеризуется также следующим свойством: прямолинейный отрезок, соединяющий любые две точки плоскости, лежащие внутри многоугольника, не пересекает многоугольник. Всякий выпуклый многоугольник – самонепересекающийся, но не наоборот. Например, на рис. 1, б изображён самонепересекающийся многоугольник, который не является выпуклым, т. к. отрезок $RQ$, соединяющий его внутренние точки $P$ и $Q$, пересекает многоугольник.

Важнейшие многоугольники: треугольники, в частности прямоугольные, равнобедренные, равносторонние (правильные); четырёхугольники, в частности трапеции, параллелограммы, ромбы, прямоугольники, квадраты. Выпуклый многоугольник называется правильным, если все его стороны равны и все внутренние углы равны. По стороне или радиусу описанного круга ещё в древности умели строить циркулем и линейкой правильные многоугольники в том случае, когда число сторон многоугольника равно $3·2^n, 4·2^n, 5·2^n, 3·5·2^n$, где $n$ – любое натуральное число или нуль. К. Гаусс (1801) показал, что циркулем и линейкой можно построить правильный многоугольник, когда число его сторон имеет вид $2^n·p_1·p_2·...·p_k$, где $p_1, p_2,...,p_k$ – различные гауссовы простые числа, т. е. простые числа вида $p=2^2 s +1$ ($s$ – натуральное число). Известны только пять таких чисел, а именно $3, 5, 17, 257, 65337$. Из теории Галуа следует, что никаких других правильных многоугольников, кроме указанных Гауссом, построить циркулем и линейкой невозможно.

В таблице приводятся радиус описанной окружности, радиус вписанной окружности и площадь некоторых правильных $n$-угольников со стороной $a$.

Таблица некоторых характеристик правильных n-угольников

Начиная с пятиугольника, существуют также невыпуклые правильные многоугольники, т. е. такие, что все стороны равны и каждая следующая из сторон повёрнута в одном и том же направлении на один и тот же угол по отношению к предыдущей (звёздчатые многоугольники). Все вершины такого многоугольника также лежат на одной окружности. Такова, например, пятиконечная звезда. На рис. 2 даны все правильные (как выпуклые, так и невыпуклые) многоугольники от треугольника до семиугольника.

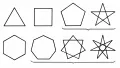Рис. 2. Правильные многоугольники.Рис. 2. Правильные многоугольники.Существуют также определения многоугольника, отличающиеся от приведённого выше. Например, многоугольником можно называть связную часть плоскости, вся граница которой состоит из конечного числа прямолинейных отрезков, называемых его сторонами. Многоугольник в этом смысле может быть многосвязной частью плоскости (рис. 1, г), т. е. такой многоугольник может иметь многоугольные дыры. Рассматриваются также бесконечные многоугольники – части плоскости, ограниченные конечным числом прямолинейных отрезков и конечным числом полупрямых.