Механи́зм (от греч. μηχανή – машина), система тел, предназначенная для преобразования движения одного или нескольких твёрдых тел в требуемые движения других тел. Если в преобразовании движения участвуют жидкие или газообразные тела, то механизмы называются соответственно гидравлическими или пневматическими. Механизмы составляют важнейшую часть большинства машин, они применяются также в приборах, аппаратах и различных технологических устройствах.

Твёрдые тела, входящие в состав механизмов и участвующие в заданном преобразовании движения, называются звеньями. Неподвижное звено механизма называется стойкой, соединение звеньев, допускающее их заданное относительное движение, – кинематической парой. Кинематические пары разделяют на 5 классов в зависимости от количества ограничений, налагаемых на относительное движение звеньев (пара $k$-класса накладывает $k$ ограничений на движение твёрдого тела). Наибольшее распространение получили пары:

• вращательная (шарнир);

• поступательная (ползун и направляющая);

• винтовая (винт и гайка);

• цилиндрическая (сочетание вращательного и поступательного движений);

• сферическая (шаровой шарнир).

Также в механизме применяют кинематические соединения, которые по характеру относительного движения заменяют кинематическую пару (например, радиально-упорный шарикоподшипник заменяет вращательную кинематическую пару).

Система звеньев механизма, образующих между собой кинематические пары, называется кинематической цепью. Кинематические цепи механизма могут быть (рис. 1) простые и сложные, разомкнутые и замкнутые, плоские и пространственные. Кинематическая цепь механизма обеспечивает определённые движения звеньев относительно неподвижного звена (стойки) при заданном движении одного или нескольких звеньев.

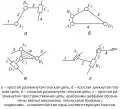Виды кинематических цепей.Виды кинематических цепей.Для изучения строения механизма и характера движения его звеньев составляется структурная схема, которая при задании размеров звеньев и других параметров образует кинематическую схему механизма, позволяющую определять положение звеньев, их скорости и ускорения. На рис. 2 показаны чертёж и кинематическая схема поршневой машины (двигателя внутреннего сгорания, компрессора и др.).

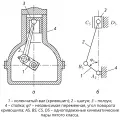Чертёж (а) и кинематическая схема (б) механизма поршневой машины.Чертёж (а) и кинематическая схема (б) механизма поршневой машины.В каждом механизме имеются входные (ведущие) и выходные (ведомые) звенья. Входному звену сообщается движение, преобразуемое механизмом в требуемое движение выходного звена. Для ведущего звена работа приложенных к нему внешних сил является положительной, для ведомого – отрицательной. Так, при работе поршневой машины (рис. 2) в качестве компрессора звено 1 является входным, звено 3 – выходным. Если же она работает как двигатель внутреннего сгорания, то ведущее и ведомое звенья меняются местами (3 – ведущее, 1 – ведомое).

Подвижность механизма характеризуется числом степеней свободы, которое равно числу независимых переменных (обобщённых координат), определяющих положение кинематической цепи механизма относительно стойки. Существуют общие закономерности в структуре (строении) различных механизмов, связывающие число степеней свободы W механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул механизмов. При выводе структурной формулы пространственного механизма для определения W учитывается процесс соединения в кинематическую цепь звеньев, которые в свободном состоянии имели бы по 6 степеней свободы, но их движение ограничено в кинематических парах (например, кинематическая пара 5-го класса накладывает на относительное движение звеньев, образующих пару, 5 связей), т. е. $$W=6n-5p_5-4p_4-3p_3-2p_2-p_1+q,$$где n – число подвижных звеньев; $p_1, p_2, p_3, p_4, p_5$ – число кинематических пар соответствующего класса; q – число избыточных (повторяющихся) связей, которые дублируют другие связи, не уменьшая подвижности механизма, а только обращая его в статически неопределимую систему. Устраняют избыточные связи заменой некоторых кинематических пар на более подвижные.

В общем виде эта формула, предложенная П. О. Сомовым и А. П. Малышевым, может быть представлена так:$$W=6n-\sum_ {i=1}^{i=5}ip_i+q_i,$$где i – номер класса кинематической пары; p – количество кинематических пар i-го класса.

Для определения числа степеней свободы плоских механизмов, в которых звенья имеют только 3 степени свободы, применяется формула, предложенная П. Л. Чебышёвым (1869): $$W=3n-2p_5-p_4.$$Для определения положения всех звеньев механизма некоторым из них задаются определённые параметры – одна или несколько обобщённых координат. Число таких звеньев, называемых начальными, равно числу степеней свободы механизма. На рис. 2 обобщённой координатой может быть угол $φ_1$, определяющий положение начального звена 1.

В рабочих машинах механизмы применяют для преобразования движения двигателя в требуемое движение исполнительного органа машины. В этом случае механизмы называются передаточными, или передачами (см. Передача в машинах). В зависимости от вида звеньев различают рычажные, зубчатые, фрикционные, цепные, ременные и другие передачи. Каждая из видов передач имеет разновидности. Например, зубчатая передача может быть с неподвижными осями зубчатых колёс, с подвижными (планетарная), с коническими колёсами и др.

Для выполнения работ в средах, недоступных или опасных для человека (подводные глубины, космос, атомные реакторы), применяются манипуляторы, основу которых составляют пространственные механизмы со многими степенями свободы. Манипуляторы также широко применяются в промышленных роботах, позволяющих автоматизировать процессы обработки, монтажа и сборки изделий.