Трисекция угла
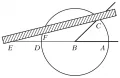
Трисе́кция угла́ (от лат. tri-, в сложных словах – три и sectio – разрезание, рассечение), задача о разделении угла на три равные части. Наряду с двумя классическими задачами, рассматривавшимися математиками Древней Греции, – квадратурой круга и удвоением куба – задача о трисекции угла сыграла большую роль в развитии математики. Первоначально решение задачи о трисекции угла стремились найти с помощью простейших геометрических средств – циркуля и линейки (без делений, с её помощью можно проводить прямые линии), что удавалось, однако, лишь в отдельных случаях (например, для углов в и , где – натуральное число). Строгое доказательство невозможности точной трисекции угла в общем случае с помощью циркуля и линейки (оно сводится к доказательству неразрешимости в квадратичных радикалах некоторого кубического уравнения) было дано французским математиком П. Ванцелем в 1837 г. Задача о трисекции угла становится разрешимой, если расширить средства построения. Так, в сочинении Архимеда трисекция угла производится с помощью т. н. приёма вставки, для которого нужны циркуль и линейка с делениями. Именно, решение задачи о трисекции угла сводится к вставке отрезка (для этого отрезок отмечается на линейке) между продолжением диаметра и окружностью так, чтобы продолжение прошло через точку , тогда .