Тео́рия зада́чного простра́нства Нью́элла и Са́ймона (англ. Problem space theory), разработанная А. Ньюэллом и Г. Саймоном теория, согласно которой мышление человека осуществляется на основе символов и системы правил, применяемой к ним. Теория предполагает, что мышление опирается на те же принципы, которые регулируют поведение, а разница между естественным мышлением человека и искусственным интеллектом машины сильно преувеличена: для машины символами являются 0 и 1, а для человека – язык, усвоенный в рамках культуры. Подобный взгляд на познавательные процессы человека принято называть компьютерной метафорой. Опора на данную метафору позволяет строить единую теорию как для искусственных, так и для естественных интеллектуальных систем, поскольку становится неважно, на каком субстрате происходят вычисления, необходимые для решения задачи. Человек при этом рассматривается как рациональный решатель: и его поведение, и его мотивация соответствуют цели и требованиям задачи (Newell. 1972). В самом общем смысле поведение связано с системой правил, призванных направить активность человека в нужное русло для достижения цели. Выбор поведения осуществляется на основе того, какие действия осуществлялись раньше и какие результаты были получены. Система правил задаётся такими факторами, как пространство задачи, доступные операторы, эвристики, ограничения задачи, состояния задачи.

Пространство задачи

Пространство задачи (задачное пространство, problem space) – пространство, внутри которого осуществляются действия по решению задачи. Различают объективное и субъективное пространство задачи. Под объективным пространством задачи понимается описание всех возможных вариантов развития событий в рамках проблемной ситуации. Субъективное пространство описывает лишь некоторые варианты ситуации; оно складывается за счёт того, что элементы задачи (инструкции, последовательность символов, доступные манипуляции с объектами задачи и др.) включены в репрезентацию решателя. Репрезентация – это вариант интерпретации ситуации решателем. Для объяснения репрезентации А. Ньюэлл и Г. Саймон приводят следующий пример. Допустим, мы хотим сыграть в числовой «Скрэббл». Это игра со следующими правилами: есть набор из девяти карточек, на каждой из которых написано целое число от 1 до 9. Каждый игрок по очереди вытягивает карточку, а выигрывает тот, кто первым соберёт три карточки, чья сумма цифр будет равна 15. Если все карточки выбраны, но ни у одного игрока нет нужной тройки, то игра заканчивается вничью. Так, игрок может выиграть, если собрал карточки 2 + 4 + 9 = 15. Описанная ситуация является объективной в том смысле, что описывает стимулы, доступные всем игрокам, имеющим зрение, слух и умение считать. Но есть и субъективная сторона данной задачи – внутренняя репрезентация решателя. Решатель может по-разному представлять данную задачу: он может считать, что для победы необходимо собрать три карточки с цифрой 5, а также при наличии у него карточек с цифрами 3 и 9 искать ещё одну карточку с цифрой 3. Кроме того, он может включать в игру факторы, которые изначально не фигурировали в задачном пространстве. К примеру, считать, что вытягивать карточки можно только правой рукой. Репрезентация индивидуальна для каждого человека, в зависимости от прошлого опыта и текущей ситуации в неё включаются или исключаются различные её свойства. Ситуация, когда репрезентация не содержит доступного варианта ответа, считается тупиковой, а подобная репрезентация описывается как неверная.

Согласно А. Ньюэллу и Г. Саймону, задача – это цель, которую решатель хочет достичь, стартуя с того исходного состояния, в котором находится. Задачное пространство организовано относительно цели задачи. Оно содержит различные элементы: объекты задачи, доступные действия (операторы или ментальные операторы, если они выполняются в мысленном плане), условия и цель, после достижения которой решение остановится или пространство задачи должно будет измениться под следующую цель. В качестве объектов могут выступать и реальные, физические объекты (яблоко, корзинка, лодка), и абстрактные символы, и понятия. Точно также действия могут быть поделены на физические (достать яблоко, нести корзинку, грести вёслами), перцептивные (смотреть, прислушаться) и мыслительные (запомнить, проанализировать).

Когда решатель сталкивается с задачей, ему доступна конкретная информация: что надо найти, какие средства, действия, операции и ресурсы можно использовать для поиска искомого, с какой исходной информации можно начать поиск и т. д. Так как решатель интерпретирует ситуацию и строит пространство задачи, то всю полученную информацию он может разделить на условия задачи (доступные средства и имеющиеся ограничения) и цель (искомое). Для исследовательских целей процесс решения задачи удобнее описывать как набор промежуточных репрезентаций, которые возникают по ходу решения по мере того, как решатель двигается от исходного состояния к целевому.

Вся совокупность возможных путей решения задачи образует дерево решений. Начальная точка дерева (исходное состояние) – это начало решения задачи со всеми доступными ходами, которые мы можем сделать из этой точки. Доступные ходы образуют варианты продвижения к решению задачи или ветви дерева. Выбирая одну из ветвей, мы ограничиваем наши дальнейшие выборы, т. к. теперь не все варианты, что были вначале, доступны для дальнейшего продвижения по ветвям дерева. Некоторые ветви дерева приводят к цели, другие – нет. Существуют деревья, в которых ни одна ветвь не может привести к искомому. Подобные «нерешаемые» деревья требуют либо пересмотра условий и цели задачи, либо предварительной подготовки, получения дополнительных знаний для добавления новых ветвей.

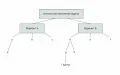Дерево решений. Архив БРЭ.Дерево решений. Архив БРЭ.

Операторы

Оператор (operator) – это правила преобразования, которыми можно воспользоваться для изменения текущего состояния, чтобы приблизиться к цели. Операторы применяются к объектам задачи или их свойствам и соотношениям и переводят решателя от одной репрезентации задачи к последующей.

Есть несколько способов научения операторам.

1. Открытие предполагает, что решатель самостоятельно узнаёт что-то об окружающем его мире и способах взаимодействия с ним, тем самым осваивая новый оператор. Открытие может быть как целенаправленным, так и случайным. Например, решатель случайно роняет мяч и узнаёт, что предметы можно бросать.

2. Решателю может быть передана та или иная информация, и он усваивает её в ходе обучения. Этот способ подразумевает вербальную передачу информации. Например, решателю сообщают о том, что некоторые предметы можно бросать, а с другими лучше не делать подобного.

3. Наблюдение с помощью зрительного анализатора позволяет усвоить оператор, который использовали другие решатели, а затем воспроизвести его на доступном материале. Например, решатель видел, как кто-то другой бросил мяч, но при этом наблюдение не сопровождалось вербальной инструкцией.

4. Аналогия во многом схожа с наблюдением, но предполагает более отдалённое сходство объектов, доступных для применения того или иного оператора. Оператор в данной ситуации известен для одной группы объектов, но сначала кажется неприменимым к другой. Примером аналогичного переноса может быть забивание гвоздя кирпичом, т. к. молоток отсутствует.

Для выбора наилучшего оператора в имеющейся ситуации можно было бы применить простой перебор всех возможных вариантов, но этот путь слишком долог для решения большинства задач. В связи с этим А. Ньюэлл и Г. Саймон предлагают способ сокращения задачного пространства – применение эвристик.

Эвристики

Эвристика (heuristic) – это часть знаний решателя, которая помогает ему ориентироваться в задаче, сокращать количество перебираемых вариантов и возможных путей решения, отсекать всё лишнее и сосредоточиться на одной из множества стратегий решения. Авторами были описаны следующие виды эвристик:

• эвристика восхождения (hill climbing). Решатель стремится достичь цели за наименьшее количество шагов и старается выбирать те операторы, которые максимально приближают его к цели. Данная эвристика существенно сокращает выбор возможных путей решения, но в ней оценивается только следующий от текущего шаг, без анализа дальнейших действий (Андерсон. 2002). Кроме того, эта эвристика вызывает трудности при необходимости вернуться на несколько шагов назад, т. к. это действие временно отдаляет решателя от цели (Thomas. 1974; Chronicle. 2004). Применение эвристики в подобной ситуации может привести решателя в тупик (Ohlsson. 1992);

• эвристика анализа средств и целей (means-ends analysis). Данная эвристика также направлена на уменьшение различий между текущим состоянием и целью, но движение в задачном пространстве должно осуществляться в обратном направлении – от цели к имеющимся у решателя средствам. Если средство не может быть доступно в данный момент времени, то оно не отбрасывается, а становится подцелью. Таким образом, движение в пространстве задачи разбивается на множество подцелей, а цель будет достигнута только после выполнения всех подцелей;

• аналогия (analogy) – попытка решить задачу с помощью информации, полученной при работе над другой задачей. Аналогия может быть как буквальным переносом решения (использование способа решения из примера в учебнике), так и довольно сложной мыслительной операцией, в которой для переноса выбирается лишь определённое свойство другого решения (например, согласно легенде, Б. Франклин придумал громоотвод, наблюдая за тем, как летит воздушный змей);

• планирование (planning). Данная эвристика создаёт общее представление о возможном общем результате решения без работы над конкретными деталями. Планирование является антиподом для эвристики анализа средств и целей, т. к. последняя позволяет видеть ситуацию только на один шаг вперёд. Планирование содержит: абстрагирование через избегание деталей у имеющихся объектов и операторов; формулирование цели и подцелей; перенос плана решения абстрактной, упрощённой проблемы на оригинальную задачу.

В своей более поздней работе Г. Саймон в соавторстве с К. Капланом (1990) дополнительно выделил такие эвристики, как:

• обращение внимания на инварианты (noticing invariants). Данная эвристика используется, когда решателю кажется, что имеющаяся репрезентация задачи не содержит решения. В таком случае для нахождения решения необходимо переключиться на иную репрезентацию задачи, представить её элементы и условия иначе. Например, числовой «Скрэббл» можно представить в виде игры в «крестики-нолики». Подобное представление задачи может подсказать решателю новые идеи;

• формулирование гипотез (forming hypotheses). Формулирование гипотез или предположений о том, каким может быть решение, также можно рассматривать в качестве эвристики. Дело в том, что наличие гипотезы существенно сокращает пространство поиска, т. к. теперь в качестве доступных ветвей решения рассматриваются только те, что соответствуют выдвинутому предположению;

• сравнение альтернатив (comparing alternative). Данная эвристика – общая, метаэвристика. Она описывает ситуацию, когда решатель сравнивает между собой ветви дерева решения, чтобы выбрать, по какой из них лучше двигаться. Сравнение альтернатив может сочетаться с другими эвристиками, которые выступают в качестве критерия сравнения. Сравнение часто происходит в задачах, аналогичных шахматам: решателю одновременно доступны несколько ветвей, но необходимо определить, какая из них даст наилучший результат.

Ограничения задачи

При решении любой задачи формируются ограничения (problem constraint) на использование тех или иных операторов, объектов и т. д. Ограничения являются неотъемлемой частью любой задачи и могут быть результатом как репрезентации исходного состояния, так и репрезентации цели. Ограничения задачи сужают возможности поиска решения (search constraint) или даже делают его невозможным. В более поздней работе Г. Саймон совместно с К. Капланом (1990) выделил четыре основных источника ограничений поиска:

• собственно свойства задачи. Решатель может не замечать некоторых свойств объектов задачи или считать их нерелевантными, неважными для поставленной цели;

• подсказки экспериментатора. Экспериментатор может указывать решателю на те или иные свойства объектов, сами объекты, доступные операторы. Тем самым экспериментатор ограничивает поиск решателя, т. к. последний уделяет существенно больше внимания указанным обстоятельствам;

• релевантные специальные знания (domain knowledge). В зависимости от того, какими знаниями обладает решатель, он может по-разному построить процесс поиска решения. Если решателю кажется, что его специальные знания полезны и применимы к решению задачи, он будет существенно дольше искать решение именно в этой плоскости. Влияние специальных знаний на процесс решения может быть как позитивным (When the solution is on the doorstep. 2019), так и негативным (Bilalić. 2008);

• эвристики. В зависимости от того, какие эвристики использует решатель, он получает различный результат. Некоторые эвристики подходят для решения задачи, позволяя быстро и легко найти ответ, другие же кажутся разумными, но в реальности заводят в тупик. Подобная ситуация была описана выше при описании эвристики восхождения.

Выделенные источники ограничений поиска, в свою очередь, можно поделить на внешние и внутренние, где внешними источниками будут свойства задачи и подсказки экспериментатора, а внутренними – специальные знания и эвристики решателя.

Состояния задачи

Состояние задачи – это описание того, о каком моменте в процессе решения идёт речь. В теории А. Ньюэлла и Г. Саймона выделяют три основных типа состояний.

1. Исходное состояние задачи формируется на основе того, какая конкретная информация дана решателю: что у него есть для решения и в каком количестве. Исходное состояние тесно связано с условиями задачи, является интерпретацией имеющихся условий, репрезентацией доступных данных.

2. Целевое состояние задачи предполагает, что у решателя есть репрезентация того, какого конечного состояния он хочет или должен достичь, т. е. решатель знает, когда задача будет считаться выполненной. Целевые состояния можно разделить на три большие группы:

   а) требуется сравнить пару объектов с целью преобразовать один объект в другой. К примеру, в ситуации, когда требуется перекрасить машину, цвет машины – объект изменения. Для достижения цели необходимо мысленно сравнить старый цвет машины с новым, а также с ожиданиями относительно нового цвета. Сравнение со старым цветом поможет понять, перекрашена машина или нет, а сравнение с желаемым новым – степень совпадения текущего состояния с целевым;

   б) требуется определить, применим ли оператор к объекту, и, возможно, преобразовать объект так, чтобы оператор стал применим. Если использовать пример с перекрашиванием машины, то необходимо понять, может ли машина быть перекрашена в текущий момент времени, какие шаги нужно сделать, чтобы перекрашивание стало доступным;

   в) требуется уменьшить различия между парой объектов, но не преобразовать один из них в другой. Например, человек может принять решение перекрасить машину не просто так, а потому, что заметил подобный цвет машины у знакомого. В этом случае цель – не преобразовать его машину в машину знакомого, а только сблизить данные объекты по одному из признаков.

   Таким образом, внутри одной большой цели (перекрасить машину) могут быть подцели, каждая из которых может относиться к разным группам целей, выделенным А. Ньюэллом и Г. Саймоном.

3. Текущее состояние задачи – все промежуточные состояния задачи при продвижении решателя от исходного к целевому состоянию.

Таким образом, теория задачного пространства говорит о том, что решение задачи – это поиск пути в пространстве задачи через последовательное применение операторов, которые приводят решателя из исходного состояния в целевое. Применяя оператор к объектам задачи, мы изменяем текущее состояние, продвигая его либо в сторону целевого состояния, либо к тупику, т. к. не все пути в пространстве задачи одинаково ведут к цели. Пути в задачном пространстве отличаются успешностью или неуспешностью, длинной, доступностью операторов, соответствием или несоответствием здравому смыслу (Atwood. 1976).

Теория задачного пространства получила множество подтверждений как в рамках экспериментальных исследований мышления человека (Андерсон. 2002; Котовский. 2008; Chase. 1973; Thomas. 1974; Chi. 1981; Rumelhart. 1977), так и в рамках компьютерных программ, решающих логические задачи (Newell. 1972; Anderson. 1997; Laird. 1987).