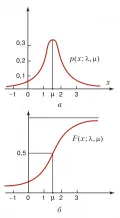
Распределе́ние Коши́, распределение вероятностей случайной величины $X$, имеющее плотность $$p(x; \lambda, \mu)={1 \over\pi}\frac{\lambda}{\pi\lambda^2+(x-\mu)^2},\quad -∞<х<∞,$$где $-∞<μ<∞$ и $λ>0$ – параметры. Распределение Коши унимодально и симметрично относительно точки $x=μ$, являющейся модой и медианой этого распределения [на рис. а и б изображены графики плотности $p(x; λ, μ)$ и соответствующей функции распределения $F(x; λ, μ)$ при $μ=1,5$ и $λ=1$]. Математическое ожидание распределения Коши не существует. Характеристическая функция распределения Коши равна $e^{iμt-λ|t|}$, $-\infty \lt t \lt \infty$. Произвольное распределение Коши с параметрами $μ$ и $λ$ выражается через стандартное распределение Коши с параметрами $0$ и $1$ формулой $$p(x;\mu,\lambda)={1 \over\lambda}p\left(\frac{x-\mu}{\lambda}\right),$$ где $$p(x)=\frac{1}{\pi(1+x^2)}\,.$$Если независимые случайные величины $X_1,\ldots,X_n$ имеют одно и то же распределение Коши, то их арифметическое среднее $(X_1+ \ldots+X_n)/n$ для любого $n=1,2,\ldots$ имеет то же самое распределение; этот факт был установлен С. Д. Пуассоном (1830). Распределение Коши является устойчивым распределением. Отношение $X/Y$ независимых случайных величин $X$ и $Y$ со стандартным нормальным распределением имеет распределение Коши с параметрами $0$ и $1$. Распределение тангенса $\tg Z$ случайной величины $Z$, с равномерным распределением на отрезке $[-π/2, π/2]$, также имеет распределение Коши с параметрами $0$ и $1$. Распределение Коши рассматривалось О. Коши в 1853 г.