Объём, одна из основных величин, связанная с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов, т. е. кубов с рёбрами, равными единице длины. В СИ объём измеряется в м³.

Задача вычисления объёмов простейших тел, идущая от практических потребностей, была одним из стимулов развития геометрии. Математика Древнего Востока (Вавилония, Египет) располагала рядом правил (большей частью эмпирических) для вычисления объёма тел, с которыми чаще всего приходилось встречаться на практике (например, призматических брусьев, пирамид полных и усечённых, цилиндров). Среди формул для вычисления объёма были и неточные, дававшие не слишком заметную ошибку лишь в пределах употребительных размеров тела. Греческая математика последних столетий до н. э. освободила теорию вычисления объёма от приближённых эмпирических правил. В «Началах» Евклида и в сочинениях Архимеда имеются только точные правила для вычисления объёма многогранников и некоторых круглых тел (цилиндра, конуса, шара и их частей). При этом в создании учения об объёме многогранников греческие математики должны были преодолеть значительные трудности, существенно отличающие этот раздел геометрии от родственного ему раздела о площадях многоугольников. Источник различия, как выяснилось лишь в начале 20 в., состоит в следующем: в то время как всякий многоугольник можно посредством надлежащих прямолинейных разрезов и перекладывания полученных частей «перекроить» в квадрат, аналогичное преобразование (посредством плоских разрезов) произвольного многогранника в куб оказывается, вообще говоря, невозможным (теорема Дена, 1901). Отсюда становится ясным, почему Евклид уже в случае треугольной пирамиды был вынужден прибегнуть к бесконечному процессу последовательных приближений, пользуясь при доказательстве методом исчерпывания. Бесконечный процесс лежит и в основе современной трактовки измерения объёма, сводящейся к следующему. Рассматриваются всевозможные многогранники, вписанные в тело $K$, и всевозможные многогранники, описанные вокруг тела 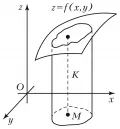$K$. Рис. 1. Объём.Рис. 1. Объём.Вычисление объёма многогранника сводится к вычислению объёмов составляющих его тетраэдров (треугольных пирамид). Пусть $\{V_\alpha\}$ – множество чисел, состоящее из объёмов вписанных в тело многогранников, а $\{V_\beta\}$ – множество чисел, состоящее из объёмов описанных вокруг тела $K$ многогранников. Множество $\{V_\alpha\}$ ограничено сверху (например, объём любого описанного многогранника), а множество $\{V_\beta\}$ ограничено снизу (например, числом нуль). Наименьшее из чисел, ограничивающее сверху множество $\{V_\alpha\}$, называется нижним объёмом $\underline V$ тела $K$, а наибольшее из чисел, ограничивающее снизу множество $\{V_\beta\}$, называется верхним объёмом $\overline V$ тела $K$. Если верхний объём тела $K$ совпадает с его нижним объёмом $\underline V$, то число $V=\overline V= \underline V$ называется объёмом тела $K$, а само тело – кубируемым телом. Для того чтобы тело было кубируемым, необходимо и достаточно, чтобы для любого положительного числа $\varepsilon$ можно было указать такой описанный вокруг тела многогранник и такой вписанный в тело многогранник, разность $V_\beta -V_\alpha$ объёмов которых была бы меньше $\varepsilon$.

Аналитически объём может быть выражен с помощью кратных интегралов. Пусть тело $K$ (рис. 1) ограничено цилиндрической поверхностью с параллельными оси $Oz$ образующими, квадрируемой областью $M$ плоскости $Oxy$ и поверхностью $z=f(x,y)$, которую любая параллель к образующей цилиндра пересекает в одной и только в одной точке. Объём такого тела может быть вычислен с помощью двойного интеграла

$\displaystyle v=\iint\limits_M f(x,y)dxdy.$Объём тела, ограниченного замкнутой поверхностью, которая пересекается с параллелями к оси $Oz$ не более чем в двух точках, может быть вычислен как разность объёмов двух тел, подобных предшествующему. В общем случае объём тела может быть выражен в виде тройного интеграла 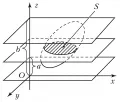$\displaystyle v=\iiint \ dxdydz,$Рис. 2. Объём.Рис. 2. Объём.где интегрирование распространяется на часть пространства, занятую телом. Иногда удобно вычислять объём тела через его поперечные сечения. Пусть тело, содержащееся между плоскостями $z=a$ и $z=b$, $b>a$, рассекается плоскостями, параллельными оси $Oz$ (рис. 2). Если все сечения тела квадрируемы и площадь сечения $S=S(z)$ – непрерывная функция $z$, то объём тела может быть выражен интегралом$\displaystyle V=\int^{b}_{a}S(z)dz.$Об обобщениях понятия объёма см. в статье Мера множества.