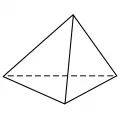
Тетра́эдр (греч. τετράεδρον, буквально – четырёхгранник; от τετρα- – часть сложных слов, обозначающая четыре, и ἕδρα – основание, грань), один из пяти типов правильных многогранников. Имеет 4 грани (треугольные), 6 рёбер, 4 вершины (в каждой вершине сходятся 3 ребра). Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Объём тетраэдра равен $$V= \frac{\sqrt{2}}{12} a^3\approx 0,1178a^3,$$где $a$ – длина ребра. Площадь поверхности тетраэдра равна площади одной его треугольной грани, умноженной на 4, и вычисляется по формуле

$$S= \sqrt 3 a^2.$$Перпендикуляр, опущенный из вершины тетраэдра на плоскость его основания, называется высотой тетраэдра. Длину этого перпендикуляра также называют высотой тетраэдра. Высота тетраэдра определяется по следующей формуле:

$$h= \frac{ \sqrt 6 }{3} a.$$Тетраэдр может быть вписан в сферу, при этом каждая из его вершин будет касаться внутренней стенки сферы. Радиус $R$ описанной сферы тетраэдра определяется по формуле:

$$R= \frac{\sqrt 6}{4} a.$$Сфера может быть вписана внутрь тетраэдра. Радиус $r$ вписанной в тетраэдр сферы определяется по формуле:

$$r= \frac{\sqrt 6}{12} a.$$Тетраэдр – правильная треугольная пирамида, одно из 5 Платоновых тел.

Иногда геометрические тела, составленные не из правильных треугольников, тоже называют тетраэдрами, т. к. они имеют четыре грани, но встречаются они редко. Другие виды тетраэдров: прямоугольный тетраэдр, у которого все рёбра, прилежащие к одной из вершин, перпендикулярны между собой; равногранный тетраэдр, у которого все грани – равные между собой треугольники; ортоцентрический тетраэдр, у которого все высоты пересекаются в одной точке; инцентрический тетраэдр, у которого отрезки, соединяющие вершины с центрами вписанных в противоположные грани окружностей, пересекаются в одной точке.