Лине́йчатая пове́рхность, поверхность, образуемая совокупностью прямых, зависящих от одного параметра. Линейчатую поверхность можно описать движением прямой (образующей) по некоторой линии (направляющей). Линейчатые поверхности разделяются на развёртывающиеся и косые.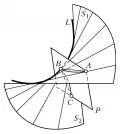Рис. 1.Рис. 1.

Развёртывающиеся линейные поверхности могут быть посредством изгибания наложены на плоскость. Любая развёртывающаяся поверхность является либо цилиндром, либоконусом, либо поверхностью, состоящей из касательных к некоторой пространственной кривой $L$ (рис. 1). Эту кривую называют ребром возврата развёртывающейся поверхности. Плоскость $P$, пересекающая ребро возврата $L$, образует в сечении с поверхностью кривую $ABC$ с точкой возврата $B$. Ребро возврата является особой линией развёртывающейся поверхности, вдоль которой две её полости $S_1$ и $S_2$ касаются друг друга. Развёртывающиеся поверхности характеризуются также тем, что касательная плоскость к ним в различных точках одной и той же образующей неизменна. Совокупность всех касательных плоскостей развёртывающейся линейчатой поверхности представляет собой однопараметрическое семейство. Иначе говоря, развёртывающаяся линейчатая поверхность является огибающей однопараметрического семейства плоскостей.

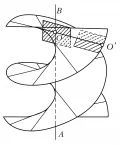Рис. 2.Рис. 2.У косой линейчатой поверхности касательные плоскости в различных точках одной и той же образующей различны. При перемещении точки касания вдоль образующей касательная плоскость вращается вокруг образующей. Полный поворот касательной плоскости, когда точка касания проходит всю образующую, равен 180°. На каждой образующей имеется точка, такая, что для каждой из двух частей, на которые она делит образующую, полный поворот касательной плоскости равен 90°. Эту точку (на рис. 2 точка $O$) называют центром образующей. Тангенс угла между касательными плоскостями к поверхности в центре $O$ и какой-либо другой точке $O'$ той же образующей пропорционален расстоянию $OO'$. Абсолютная величина гауссовой кривизны линейчатой поверхности достигает на данной образующей наибольшего значения в центре образующей и убывает при удалении от центра по образующей. Множество центров образующих называется линией сжатия или стрикционной линией. Например, у геликоида (линейчатой поверхности, описываемой равномерным винтовым движением прямой вокруг некоторой оси, которую движущаяся прямая пересекает под прямым углом) линией сжатия является ось ($AB$ на рис. 2). Линейчатые поверхности 2-го порядка – гиперболический параболоид, однополостной гиперболоид – имеют две различные системы прямолинейных образующих (из однополостных гиперболоидов сконструирована радиомачта системы В. Г. Шухова, находящаяся в Москве на Шаболовке). Две системы прямолинейных образующих имеют только линейчатую поверхность 2-го порядка.

Изгибаемые друг на друга линейчатые поверхности можно катить одну по другой так, что в процессе качения они будут иметь общую образующую. На этом основано применение линейчатой поверхности в теории механизмов.