Граф (в математике), множество $V$ вершин и набор $E$ неупорядоченных и упорядоченных пар вершин; обозначается граф через $G(V,E)$. Неупорядоченная пара вершин называется ребром, упорядоченная пара – дугой. Граф, содержащий только рёбра, называется неориентированным; граф, содержащий только дуги, – ориентированным. Пара вершин может соединяться двумя или более рёбрами (дугами одного направления), такие рёбра (дуги) называются кратными. Дуга (или ребро) может начинаться и кончаться в одной и той же вершине, такая дуга (ребро) называется петлёй. (Иногда под графом понимают граф без петель и кратных рёбер; тогда граф, в котором допускаются кратные рёбра, называется мультиграфом, а граф, в котором допускаются кратные рёбра и петли, называется псевдографом.)

Вершины, соединенные ребром или дугой, называются смежными. Рёбра, имеющие общую вершину, также называют смежными. Ребро (дуга) и любая из его двух вершин называются инцидентными. Говорят, что ребро $(u, v)$ соединяет вершины $u$ и $v$, а дуга $(u, v)$ начинается в вершине $u$ и кончается в вершине $v$.

Каждый граф можно представить в евклидовом пространстве множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими рёбрам (или дугам) графа. В трёхмерном пространстве любой граф можно представить таким образом, что линии, соответствующие рёбрам (дугам), не пересекаются во внутренних точках.

Существуют различные способы задания графа. Пусть $u_1, u_2, \ldots, u_n$ – вершины графа $G(V, E)$, а $e_1, e_2, \ldots e_n$ – его рёбра. Матрицей смежности, соответствующей графу $G$, называется матрица $A=\|a_{ij}\|$, у которой элемент $a_{ij}$ равен числу рёбер (дуг), соединяющих вершины $u_i$ и $u_j$ (идущих из $u_i$ в $u_j$), и $a_{ij}=0$, если соответствующие вершины не смежны. В матрице инцидентности $B=\|b_{ij}\|$ графа $G$ элемент $b_{ij}=1$, если вершина $u_i$ инцидентна ребру $e_j$, и $b_{ij}=0$, если вершина $u_i$ и ребро $e_j$ не инцидентны. Граф можно задать посредством списков, например, указанием пар вершин, соединённых рёбрами (дугами), или заданием для каждой вершины множества смежных с ней вершин. Два графа $G(V, E)$ и $H(W, I)$ называются изоморфными, если существует взаимно однозначное соответствие между множествами вершин $V, W$ и множествами рёбер $E, I$, сохраняющее отношение инцидентности.

Подграфом $G'(V', E')$ графа $G(V, E)$ называется граф с множеством вершин $V'\subseteq V$ и множеством рёбер (дуг) $E'\subseteq E$, каждое из которых инцидентно только вершинам из $V'$. Подграфом $G'(V', E')$, порождённым подмножеством $V'\subseteq V$, называется граф с множеством вершин $V'$ и набором рёбер (дуг) $E'$, состоящим из всех рёбер (дуг) графа $G$, которые соединяют вершины из $V'$. Остовный подграф $G'(V, E')$ содержит все вершины графа $G$ и некоторый поднабор его рёбер (дуг) $E'\subseteq E$. Последовательность рёбер $(u_0, u_1)$, $(u_1, u_2), \ldots$, $(u_{i-1}, u_i)$, $(u_i, u_{i+1}), \ldots$, $(u_{r-1}, u_r)$ называется маршрутом, соединяющим вершины $u_0$ и $u_r$. Маршрут замкнут, если $u_0=u_r$. Маршрут называется цепью, если все его рёбра различны, и простой цепью, если все его вершины различны. Замкнутая (простая) цепь называется (простым) циклом. Граф называется связным, если любая пара его вершин соединена маршрутом. Максимальный связный подграф графа $G$ называется компонентой связности. Несвязный граф имеет по крайней мере две компоненты связности.

Длина маршрута (цепи, простой цепи) равна количеству рёбер в порядке их прохождения. Длина кратчайшей простой цепи, соединяющей вершины $u_i$ и $u_j$, в графе $G$, называется расстоянием $d(u_i, u_j)$ между $u_i$ и $u_j$. В связном неориентированном графе расстояние удовлетворяет аксиомам метрики. Диаметр графа – это его наибольшее расстояние. Величина $\min\limits_{u_i}\max\limits_{u_j}d(u_i, u_j)$ называется радиусом, а вершина $u_0$, для которой $\max\limits_{u_j}d(u_i,u_j)$ принимает наименьшее значение, называется центром графа $G$. В графе может быть много центров и ни одного.

Степенью вершины $u_i$ графа $G$, обозначаемой $d_i$, называется число рёбер, инцидентных этой вершине. Если граф $G$ (без петель) имеет $n$ вершин и $m$ рёбер, то $\displaystyle\sum_{i=1}^nd_i=2m$. Вершина называется изолированной, если $d_i=0$, и концевой, если $d_i=1$. Граф, у которого все вершины имеют одинаковые степени (равные $k$), называется регулярным (степени $k$). В полном графе нет петель и каждая пара вершин соединена в точности одним ребром. Для графа $G(V, E)$, не имеющего петель и кратных рёбер, дополнительным графом к $G$ называется граф $\overline{G}(\overline{V}, \overline{E})$, у которого $\overline{V}=V$ и вершины смежны в $\overline G$ только в том случае, когда они не смежны в $G$. Граф, дополнительный к полному, состоит из изолированных вершин и называется пустым. Многие характеристики для графа $G$ и его дополнения $\overline G$ оказываются зависимыми. В ориентированном графе $G$ для каждой вершины $u_i$ определяются полустепень исхода и полустепень захода как количества дуг, выходящих из этой вершины и входящих в неё соответственно. Полный ориентированный граф называется турниром.

Каждому графу $G$ можно отнести ряд графов, являющихся производными от $G$. Так, рёберным графом $L(G)$ графа $G$ называется граф, вершины которого соответствуют рёбрам графа $G$ и две вершины смежны в $L(G)$ в том и только в том случае, когда соответствующие им рёбра графа $G$ смежны. В тотальном графе $T(G)$ графа $G$ вершины соответствуют элементам графа $G$, т. е. вершинам и рёбрам, и две вершины в $T(G)$ смежны тогда и только тогда, когда соответствующие элементы в $G$ смежны или инцидентны. Многие свойства графа $G$ переносятся на графы $L(G)$ и $T(G)$. Известно много обобщений понятия «граф»; одними из них являются понятия гиперграфа и сети.

С помощью различных операций можно строить граф из более простых, переходить от одного графа к более простому, разбивать граф на более простые, в заданном классе графов переходить от одного графа к другому и т. д. Наиболее употребительными одноместными операциями являются: удаление ребра (вершины ребра сохраняются), добавление ребра между двумя вершинами графа, удаление вершины вместе с инцидентными ей рёбрами (граф, полученный в результате удаления вершины $v$ из графа $G$, часто обозначают $G-v$), добавление вершины (которую можно соединить рёбрами с некоторыми вершинами графа), стягивание ребра – отождествление пары смежных вершин, т. е. удаление пары смежных вершин и добавление новой вершины, смежной с теми вершинами графа, которые были смежны хотя бы с одной из удаленных вершин; подразбиение ребра – удаление ребра и добавление новой вершины, которая соединяется ребром с каждой вершиной удаленного ребра.

В ряде задач теории графов используются двуместные операции над графами. Пусть $G_1=G(V_1, E_1)$ и $G_2=G(V_2, E_2)$ – графы, такие, что $V_1\cap V_2=\varnothing$ и $E_1\cap E_2=\varnothing$. Объединением графов $G_1$ и $G_2$ называется граф $G=G_1\cup G_2$ с множеством вершин $V=V_1\cup V_2$ и множеством рёбер $E=E_1\cup E_2$. Произведением графов $G_1$ и $G_2$ называется граф $G=G_1\times G_2$, множеством вершин которого являются элементы декартова произведения $V=V_1\times V_2$, причем две из этих вершин $(u_1, u_2)$ и $(v_1, v_2)$ смежны в том и только в том случае, если либо $u_1=v_1$ и вершина $u_2$ смежна с вершиной $v_2$, либо $u_2=v_2$ и вершина $u_1$ смежна с вершиной $v_2$. Например, любой граф является объединением своих компонент связности; граф, известный как $n$-мерный единичный куб $Q_n$, может быть определен рекуррентно с помощью операции произведения: $$Q_n=K_2\times Q_{n-2},$$где $Q_1=K_2$ – граф, состоящий из пары вершин, соединенных одним ребром. Эти операции можно определить также для пересекающихся графов, в частности для подграфов одного графа. Сложением по модулю 2 графов $G_1$ и $G_2$ называется граф $G$ с множеством вершин $V=V_1\cup V_2$ и множеством рёбер $E=(E_1\cup E_2)\setminus (E_1\cap E_2)$.

Употребляются и другие многоместные операции над графами.

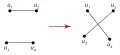Рис. 1. Операция в классе графов с одинаковым набором степеней.Рис. 1. Операция в классе графов с одинаковым набором степеней.Для некоторых классов графов удаётся найти простые операции, позволяющие с помощью многократного их применения перейти от любого графа изучаемого класса к любому другому графу этого класса. На рис. 1 приведена операция, с помощью которой в классе графов с одинаковым набором степеней можно перейти от одного произвольного графа к любому другому; на рис. 2 показана операция, позволяющая в классе плоских триангуляций (см. Плоский граф) с одинаковым числом вершин перейти от произвольной триангуляции к любой другой. Для описания и изучения некоторых классов графов отыскиваются такие операции и множества графов, из которых с помощью данных операций можно получить любой граф заданного класса. Операции над графами используются также для построения графов с заданными свойствами, при вычислении числовых характеристик графов и т. д.

Рис. 2. Операция в классе плоских триангуляций с одинаковым числом вершин.Рис. 2. Операция в классе плоских триангуляций с одинаковым числом вершин.Понятие «граф» используется в определении таких математических понятий, как управляющая система, в некоторых определениях алгоритма, грамматики и других. Изложение ряда математических теорий становится более наглядным при использовании геометрического представления графа, например теории марковских цепей. Понятие «граф» широко используется при создании и описании различных математических моделей в экономике, биологии и т. д.