Дислока́ции в кристаллах (от ср.-век. лат. dislocatio – смещение), специфические дефекты в кристаллах, представляющие собой линии, вдоль которых нарушено правильное расположение атомных слоёв.

Впервые понятие дислокации как топологического линейного источника внутренних напряжений в твёрдом теле, рассматриваемом как сплошная среда, было введено В. Вольтеррой в 1905 г. Однако наука о дислокациях начала интенсивно развиваться с 1934 г., когда Дж. И. Тейлор, Э. Орован и М. Полани впервые объяснили атомный механизм пластичности кристаллов.

Типы дислокаций

Простейшими типами дислокаций являются краевая и винтовая дислокации. Краевая дислокация представляет собой линию, вдоль которой внутри кристалла обрывается «лишняя» атомная полуплоскость (рис. 1). 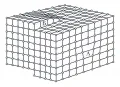Рис. 1. Краевая (А) и винтовая (Б) дислокации в кристалле. БРЭ. Т. 9.Рис. 1. Краевая (А) и винтовая (Б) дислокации в кристалле. БРЭ. Т. 9.Такая дислокация может быть получена в результате неполного сдвига верхней части кристалла на один период кристаллической решётки вдоль плоскости, проходящей через ось дислокации. Направление сдвига и его величина определяют основную характеристику дислокации – т. н. вектор Бюргерса $\boldsymbol b,$ который постоянен вдоль всей линии дислокации и нередко называется её топологическим зарядом. Если сдвиг не перпендикулярен, а параллелен оси дислокации, то она называется винтовой (рис. 1). В этом случае ни одна из атомных плоскостей не обрывается внутри кристалла, но все они смыкаются в единую винтовую поверхность. В месте выхода винтовой дислокации на внешнюю поверхность кристалла образуется ступенька. Лёгкость присоединения новых атомов к такой ступеньке обусловливает т. н. спиральный механизм ускоренного роста кристаллов. Кроме чисто краевых и винтовых дислокаций, возможны более общие комбинированные типы криволинейных дислокаций. Линии дислокаций топологически не могут обрываться внутри кристалла, они должны либо замыкаться в петли, либо разветвляться на дислокациях с другими векторами Бюргерса (но с той же их суммой), либо выходить на поверхность кристалла.

Имеются особенности строения дислокаций в кристаллах различной симметрии. Например, в объёмноцентрированных кубических (ОЦК) кристаллах ядра винтовых дислокаций могут быть расщеплены в трёх плоскостях, что в итоге приводит к асимметрии их движения в противоположных направлениях. Нередко дислокации расщепляются на частичные с меньшими векторами Бюргерса. Такое расщепление энергетически выгодно вследствие того, что энергия дислокаций пропорциональна величине вектора Бюргерса $(\sim \boldsymbol b^2).$

Искажение кристаллической структуры вблизи дислокации (т. н. ядро) охватывает область диаметром в несколько периодов кристаллической решётки. Такое искажение обусловливает возникновение дальнодействующих внутренних упругих напряжений $\sigma$ в кристалле, убывающих обратно пропорционально расстоянию $r$ от дислокации ($\sigma \sim ~ 1/r$). За пределами ядра кристаллическая решётка является локально деформированной, но топологически совершенной.

Методы наблюдения дислокаций

1. Метод избирательного (селективного) травления поверхности кристалла. Основан на том, что специально подобранная жидкость (химический реактив) быстрее растворяет материал вблизи дефекта кристалла, где атомные связи слабее. Рис. 2. Следы двойного травления поверхности кристалла NaCl до и после воздействия. Плоскодонные ямки травления (1, …, 9) отмечают стартовые позиции подвижных дислокаций до воздействия, а маленькие ямки (1', …, 9') – конечные позиции. Фото из статьи: Альшиц В. И., Даринская Е. В., Урусовская А. А., Перекалина Т. М. О движении дислокаций в кристаллах NaCl под действием постоянного магнитного поля // Физика твёрдого тела. 1987. Т. 29, вып. 2. С. 467–471.Рис. 2. Следы двойного травления поверхности кристалла NaCl до и после воздействия. Плоскодонные ямки травления (1, …, 9) отмечают стартовые позиции подвижных дислокаций до воздействия, а маленькие ямки (1', …, 9') – конечные позиции. Фото из статьи: Альшиц В. И., Даринская Е. В., Урусовская А. А., Перекалина Т. М. О движении дислокаций в кристаллах NaCl под действием постоянного магнитного поля // Физика твёрдого тела. 1987. Т. 29, вып. 2. С. 467–471.В результате возникают ямки травления, указывающие последовательные положения дислокаций в различные моменты времени (рис. 2). По числу ямок травления на единицу площади определяют плотность дислокаций.

2. Метод рентгеновской топографии. Поля напряжений дефекта деформируют кристаллическую решётку и изменяют условия прохождения рентгеновских лучей. Это отражается на интенсивности дифрагирующих лучей вблизи линии дислокации.

3. Метод просвечивающей электронной микроскопии. Монохроматические пучки электронов с энергией около 100–400 кэВ (в уникальных устройствах до 1,5 MэВ) дают возможность изучать тонкие детали дефектов в кристаллах. Электронные микроскопы с большой разрешающей способностью позволяют в настоящее время непосредственно наблюдать создаваемые дислокациями нарушения расположения атомных слоёв.

Существуют и другие специальные методы визуализации дислокаций для различных типов кристаллов.

Зарождение дислокаций

Обычно дислокации возникают уже при образовании кристалла. Выращивание бездислокационных или малодислокационных кристаллов представляет собой сложную технологическую задачу, успешно решаемую в полупроводниковой промышленности, обеспечивающей производство транзисторов, компьютерных чипов и т. п. В некоторых других производствах, наоборот, наличие некоторой плотности дислокаций полезно для обработки материалов, т. к. придаваемая дислокациями пластичность предохраняет материалы от хрупкого разрушения при изготовлении изделий.

Создание дислокаций требует довольно значительной энергии, в типичных случаях порядка 5 эВ на период решётки, поэтому дислокационная подсистема не является равновесной. Она возникает и трансформируется как реакция кристалла на внешние воздействия и всегда обеспечивает снижение совокупной энергии полей внутренних напряжений.

Рис. 3. Генерация дислокаций вблизи концентратора напряжений в пластине кремния. Фото из работы: Föll H. Defects in Crystals. Kiel University, 2019.Рис. 3. Генерация дислокаций вблизи концентратора напряжений в пластине кремния. Фото из работы: Föll H. Defects in Crystals. Kiel University, 2019.При приложении к кристаллу достаточной внешней нагрузки дислокации начинают размножаться, причём при превышении некоторого порогового значения напряжений, называемого пределом упругости, размножение приобретает массовый характер и начинается пластическое течение материала.

Источником дислокаций при размножении может быть прогибающийся между точками закрепления дислокационный сегмент или различные несовершенства кристаллической структуры, создающие концентраторы напряжений (рис. 3).

Дислокации и пластическая деформация

Приложенная извне нагрузка, взаимодействуя с полем напряжений вокруг дислокаций, приводит к их перемещению. Различают консервативное (без переноса массы) и неконсервативное движения дислокаций. Последний тип движения возможен практически вдоль любого направления (например, под острым углом к экстраплоскости краевой дислокации), но требует повышенных температур, поскольку должен сопровождаться диффузионными потоками точечных дефектов (вакансий или межузельных атомов). При умеренных температурах реализуется только консервативный тип движения путём пересоединения связей в ядре дислокации. Это возможно лишь в выделенных плоскостях, называемых плоскостями скольжения и задаваемых совокупностью направлений вектора Бюргерса и линии дислокации. Для вовлечения дислокаций в движение по плоскости скольжения нужны значительно меньшие напряжения, чем для сдвига части кристалла как целого вдоль этой плоскости при отсутствии дислокаций. Разница заключается в несопоставимом количестве разрываемых связей, чем и объясняется пластичность многих металлов, содержащих заметную плотность дислокаций.

Рис. 4. Деформация кристалла вследствие прохождения дислокации.Рис. 4. Деформация кристалла вследствие прохождения дислокации.Перемещение дислокаций на заметные расстояния приводит к необратимой (в отличие от упругой деформации) пластической деформации кристалла. При смещении дислокации на период кристаллической решётки происходит разрыв атомных связей в дислокационном ядре и пересоединение их в новом положении, эквивалентном исходному вследствие периодичности кристалла. Перемещение дислокаций приводит к изменению формы образцов (рис. 4).

Пластичность кристалла почти полностью определяется его способностью к размножению дислокаций и их подвижностью.

Динамические свойства дислокаций

Подвижность дислокаций зависит не только от типа кристалла, но и от их «возраста», поскольку дислокации являются мощным стоком для точечных дефектов: примесей, межузельных атомов, вакансий и др. Диффузионный дрейф дефектов к дислокации заканчивается созданием вокруг неё т. н. атмосферы Коттрелла, которая почти полностью закрепляет дислокацию. Именно поэтому в экспериментах по изучению подвижности дислокаций всегда предварительно вводят «свежие» дислокации (коротким импульсом напряжения, царапанием поверхности и т. п.).

Конечно, в процессе активной деформации кристалла такие атмосферы не успевают формироваться, но взаимодействие дислокации с точечными дефектами, которые она встречает на своём пути, остаётся важным фактором, определяющим её подвижность. Каждый такой локальный центр пиннинга (закрепления) дислокации характеризуется необходимой для его преодоления определённой энергией активации $U( \sigma),$ которая убывает по мере увеличения суммарного напряжения $s$, действующего на дислокацию в данном месте. Соответственно, время $\Delta t,$ требуемое на термоактивационное открепление дислокации от центра, $\Delta t \sim exp(U/k_БT),$ должно резко уменьшаться с увеличением $\sigma$ и температуры $T$ $(k_Б$ – постоянная Больцмана), что подтверждается экспериментально.

Существуют и другие механизмы торможения дислокаций при их движении. Прежде всего это т. н. рельеф Пайерлса, обусловленный дискретностью решётки: структура ядра дислокации, а значит, и его энергия должны периодически меняться при перемещении дислокации в плоскости скольжения (рис. 5). 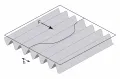Рис. 5. Флуктуационное преодоление дислокацией потенциального рельефа Пайерлса с периодом h под действием внешней силы F.Рис. 5. Флуктуационное преодоление дислокацией потенциального рельефа Пайерлса с периодом h под действием внешней силы F.Конечно, дислокация не перемещается как единое целое из одной долины рельефа в другую. Реальные дислокации содержат т. н. кинки и джоги, или, иначе, перегибы в плоскости скольжения и ступеньки вне плоскости скольжения. Эти «дефекты на дефекте» существенно влияют на подвижность дислокаций и, следовательно, на пластичность материалов. Основным зародышем консервативного движения дислокации в рельефе Пайерлса является двойной перегиб. Его возникновение обусловлено тепловыми (при высоких температурах) и квантовыми (при низких температурах) флуктуациями формы дислокационных линий, приводящими к локальным смещениям дислокационных сегментов, затем распространяющихся на всю линию.

Высота рельефа Пайерлса сильно различается в кристаллах разных типов. Считается, что он весьма высок в ОЦК-металлах и таких полупроводниках, как кремний и германий. В экспериментах по динамике дислокаций в кремнии их движение наблюдалось лишь при очень высоких температурах ~800 K. Но даже в этих кристаллах подвижность дислокаций оказалась весьма чувствительной к введению в кристалл различных примесей. При этом иногда наблюдают весьма нетривиальные эффекты, например некоторые примеси облегчают движение дислокаций. Причина заключается в том, что химическая связь этих примесей с дислокациями понижает энергию образования двойного перегиба.

Термоактивационные механизмы перемещения дислокаций характерны для относительно медленного движения, когда кинетическая энергия дислокации значительно меньше энергии активации $U$ преодоления локальных барьеров или образования двойного перегиба в рельефе Пайерлса. При высоких скоростях v (обычно выше 10 м/с), обеспечивающих надбарьерное движение дислокаций, или при их колебательных движениях между точками закрепления в переменных полях ультразвука в условиях внутреннего трения торможение дислокаций имеет вязкий характер и лимитируется взаимодействием с фононами и электронами проводимости в металлах. В этом случае справедлива оценка $v \approx b \sigma /B,$ где $B$ – константа демпфирования дислокации, возрастающая с температурой. Таким образом, в рассматриваемом динамическом режиме скорость (как и в случае медленного движения дислокаций) тоже возрастает при увеличении упругого напряжения (но линейно, а не экспоненциально) и уменьшается, а не возрастает с ростом температуры.

Влияние дислокаций на физические свойства кристаллов

Дислокации влияют не только на механические свойства кристаллических материалов, такие как прочность и пластичность, но и на многие другие фундаментальные свойства твёрдых тел. Возникновение оборванных атомных связей в ядре дислокаций может вести к захвату электронов и связанному с этим влиянию дислокаций на электрические, люминесцентные и магнитные свойства материала.

Скорость диффузионного перемещения точечных дефектов вдоль оси дислокации («трубочная диффузия»), как правило, выше, чем в объёме совершенного кристалла. Поэтому дислокации способствуют ускорению диффузионных процессов и используются для выведения из кристаллов вредных примесей. Способность дислокаций, вовлекаемых в колебательное движение, рассеивать механическую энергию приводит к заметному вкладу во внутреннее трение в твёрдых телах.

В пьезоэлектриках дислокации создают вокруг себя не только механические напряжения, но и электрическое поле напряжённостью $E$, которое нарастает по мере приближения к ядру дислокации ($\sim 1/r$), и в его окрестности $E$ может достигать весьма высоких значений: ~10⁸ В/м.

В немагнитных кристаллах наблюдают нетривиальный магнитопластический эффект, когда дислокации благодаря оборванным связям в ядре образуют радикальные пáры с примесными центрами пиннинга. В результате во внешнем магнитном поле (~1 Тл) происходит спиновая трансформация, снимающая квантовый запрет на определённый электронный переход в системе. Это, в свою очередь, приводит к существенному изменению структуры центра дислокации, уменьшению силы пиннинга и откреплению дислокации даже без приложения внешней нагрузки или повышения температуры. В частности, перемещения дислокаций, показанные на рис. 2, произошли в результате только одного внешнего воздействия на кристалл – включения магнитного поля 0,5 Тл на 2 мин.